Индивидуальная работа 3 Статистическое изучение вариации значений признаков Теоретическая часть

Для характеристики степени вариации значений признака в совокупности вычисляются следующие обобщающие показатели вариации:

- абсолютные: размах вариации (R), среднее линейное отклонение ( ), дисперсия ( ) и среднее квадратическое отклонение ( ).

- относительные: коэффициент вариации (V).

Расчет некоторых из этих показателей зависит от исходных данных: в случае не сгруппированных данных применяют простые формулы, а в случае сгруппированных данных – взвешенные (табл.3.1).

Таблица 3.1 – Формулы для расчета показателей вариации

Показатель вариации	Формула
	простая	взвешенная
Размах вариации (амплитуда изменения значений признака)
Среднее линейное отклонение
Дисперсия
Среднее квадратическое отклонение
Коэффициент вариации

Особенностью показателя дисперсии является то, что его значение имеет размерность квадрата значений признака и интерпретация его смысла затруднена. Несмотря на это показатель дисперсии имеет очень важное значение в статистике и в частности в факторном анализе.

Для интерпретации степени вариации значений признака извлекают арифметический квадратный корень из значения дисперсии, тем самым, получая показатель среднего квадратического отклонения , которое и отражает то, на сколько в среднем индивидуальные значения признака колеблются (отклоняются) от их среднего значения.

Значение среднего квадратического отклонения имеет те же единицы измерения, что и значения признака. По этой причине для сравнения степени вариации значений разных признаков, имеющих разные единицы измерения, этот показатель применить не получится.

Для решения подобной задачи исчисляют относительный показатель вариации – коэффициент вариации.

Если коэффициент вариации:

- меньше 15%, можно судить о низкой степени вариации значений признака и высокой степени однородности совокупности его значений;

- от 15% до 33%, можно судить об умеренной (средней) степени вариации значений признака и достаточной степени однородности совокупности его значений;

- 33% и более, можно судить о высокой степени вариации значений признака и неоднородности совокупности его значений.

Если выполнена аналитическая группировка совокупности единиц по какому-либо факторному признаку Х, то для оценки влияния этого фактора, определяющего колеблемость индивидуальных значений результативного признака Y, можно воспользоваться разложением дисперсии его значений на составляющие: межгрупповую и внутригрупповую дисперсии.

При дисперсионном анализе в первую очередь рассчитывают дисперсию общую, которая характеризует вариацию признака Y под влиянием всех факторов, определяющих его индивидуальные различия у единиц совокупности:

, (3.1)

где – общая дисперсия значений результативного признака Y;

– общая средняя значений признака Y, вычисленная по всей совокупности его значений;

n – число значений признака в совокупности;

– индивидуальные значения признака.

Если необходимо в составе общей дисперсии выделить ту ее часть, которая обусловлена влиянием фактора Х, положенного в основание группировки, то рассчитывают дисперсию межгрупповую (или факторную):

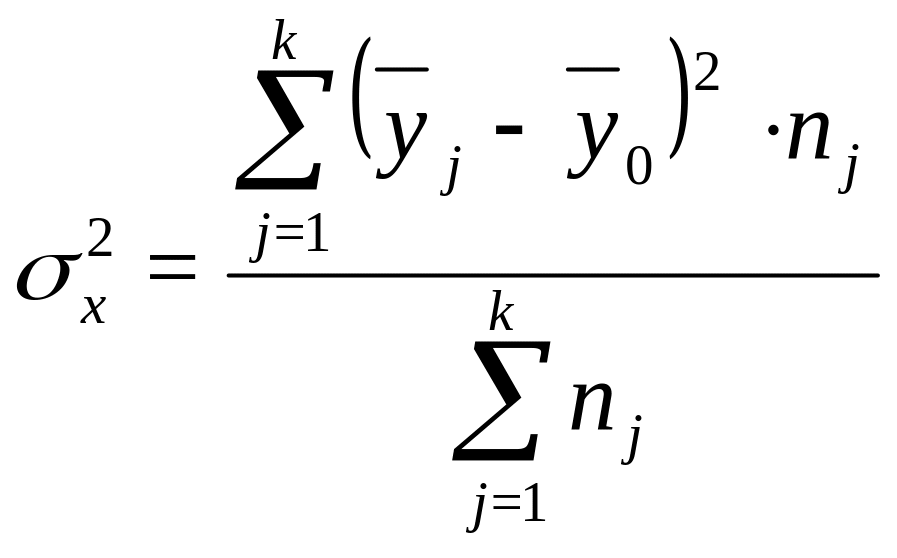, (3.2)

где – межгрупповая (факторная) дисперсия результативного признака;

– групповые средние значения Y, вычисленные по группам;

– число наблюдений в группах;

– число групп.

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия:

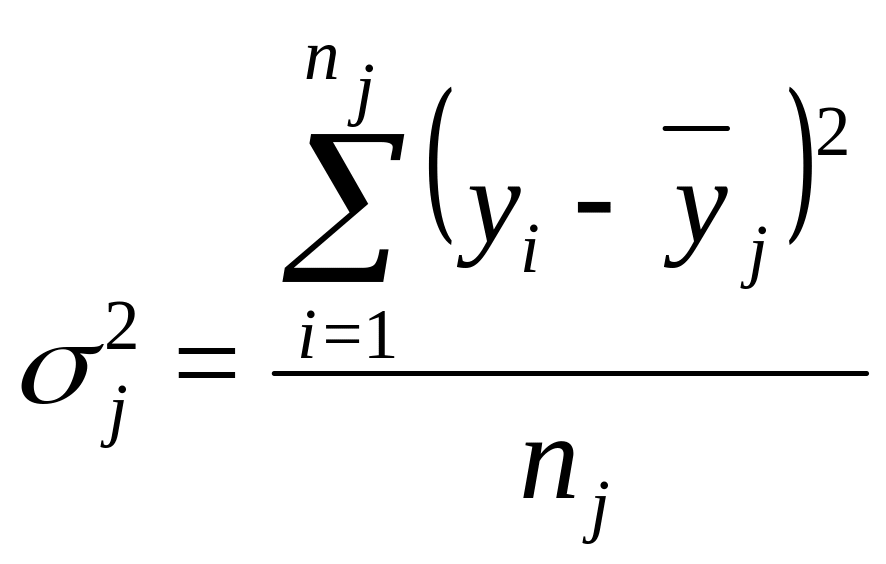, (3.3)

где – индивидуальные значения признака.

По совокупности в целом из полученных внутригрупповых дисперсий рассчитывают среднюю внутригрупповую (остаточную) дисперсию:

. (3.4)

По правилу сложения дисперсий общая дисперсия равна сумме межгрупповой и остаточной дисперсий:

. (3.5)

Если сравнение групповых средних показывает определенное различие в их уровне, то необходимо установить, является ли это различие существенным и вызвано ли оно влиянием фактора Х.

1. Формулируется проверяемая (нулевая) гипотеза Н₀ о том, что различия между групповыми средними значениями результативного признака не существенны и сформировались под влиянием случайных факторов, а значит влияние факторного признака на формирование значений результативного признака не существенно по сравнению с влиянием этих факторов.

Для этого определяют дисперсии межгрупповую и остаточную на одну степень свободы (девиации):

, (3.6)

где k - количество групп, полученных в результате группировки.

, (3.7)

где n – число значений признака в совокупности.

Полученные девиации сравнивают (большую по значению девиацию делят на меньшую) и получают расчетное значение критерия (F_расч).

По таблице F-распределения Фишера (Приложение 6) при определенном уровне значимости α (альфа) и числе степеней свободы (k₁ (соответствует большей девиации) и k₂ (соответствует меньшей девиации)) определяется табличное значение критерия (F_табл).

Если F_расч > F_табл, то следует считать, что существенное влияние признака фактора не опровергается.

По проведенному дисперсионному анализу можно определить степень тесноты связи между признаками. Для этого рассчитываются показатели: эмпирическое корреляционное отношение (η) и коэффициент детерминации (η²):

. (3.8)

Характеристика степени тесноты связи по значению величины η может быть дана на основе шкалы Чэддока (табл. 3.2).

Таблица 3.2 – Шкала Чэддока

Значения η	менее 0,1	0,1–0,3	0,3–0,5	0,5–0,7	0,7–0,9	0,9–0,99	свыше 0,99
Характеристика связи	очень слабая	слабая	умеренная	заметная	тесная	весьма тесная	функциональная

Эмпирический коэффициент детерминации η² характеризует долю факторной вариации в изменчивости значений результативного признака.

Если значение выражено в процентах, то оно показывает, на сколько процентов вариация значений результативного признака обусловлена влиянием фактора Х, положенного в основу группировки. Если полученное значение вычесть из 100%, то результат покажет долю совокупного влияния всех прочих факторов на вариацию значений результативного признака Y.