4. Теория моментов.

Момент – одна из числовых характеристик распределения вероятностей

Примечание: Распределение вероятностей какой-либо действительной случайной величины Х задается в виде конечной или бесконечной последовательности ее возможных значений: х₁, х₂, х₃,…х_n ,… и соответствующих им вероятностей Р (Х = х) : р₁, р₂, …р_n. Вероятности должны быть положительными и в сумме давать единицу.

Например, для игральной кости это будет выглядеть в виде следующей таблицы:

Возможные значения хi	1	2	3	4	5	6
Соответствующие вероятности рi	1/6	1/6	1/6	1/6	1/6	1/6

Распределение вероятностей данного типа будет называться дискретным

Момент порядка k (k>0, целое) случайной величины Х определяется как математическое ожидание ЕХ^k случайной величины Х^k , если оно существует.

Если F(Х) – функция распределения случайной величины Х, то

ЕХ^k = (1.4.1)

при условии, что интеграл сходится абсолютно. В частности, если Х принимает значения х₁, х₂, х₃,…х_n с вероятностями р₁, р₂, …р_n , то

ЕХ^k = . (1.4.2)

Если Х имеет плотность распределения f (х) на прямой, то

ЕХ^k = , f(x) dx (1.4.3)

Примечание: плотность распределения вероятностей случайной величи6ны Х функция f(x), такая, что f(x)≥0 и , а при любых a<b вероятность события a<х<b равна

Функция распределения F(Х) случайной величины Х, если она дифференцируема связана с плотностью вероятности следующим соотношением

. (1.4.4)

Величина Е(х-а)^k называется моментом порядка k относительно a, Е(х-Ех)^k - центральным моментом порядка k. Центральный момент второго порядка Е(х-Ех)² называется дисперсией DX.

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда. Различают: начальный момент порядка q (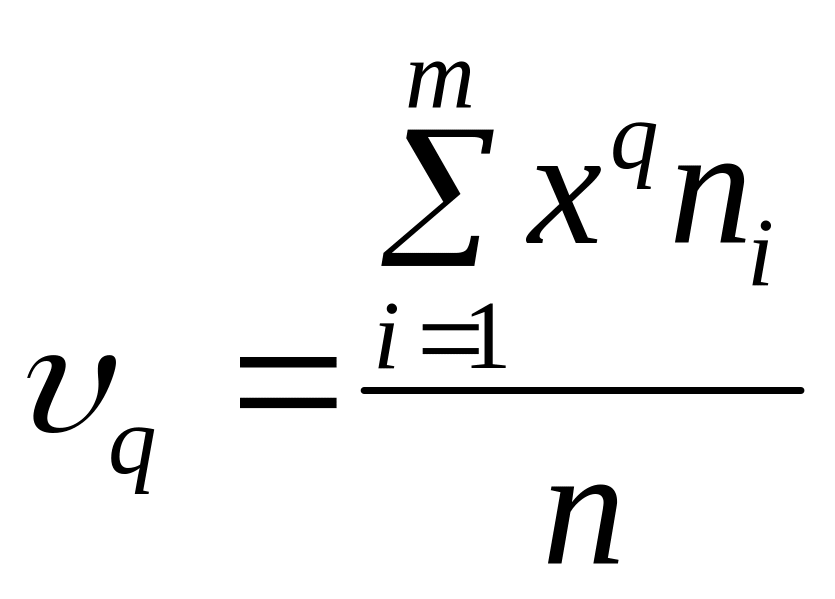 ) и центральный момент ( ).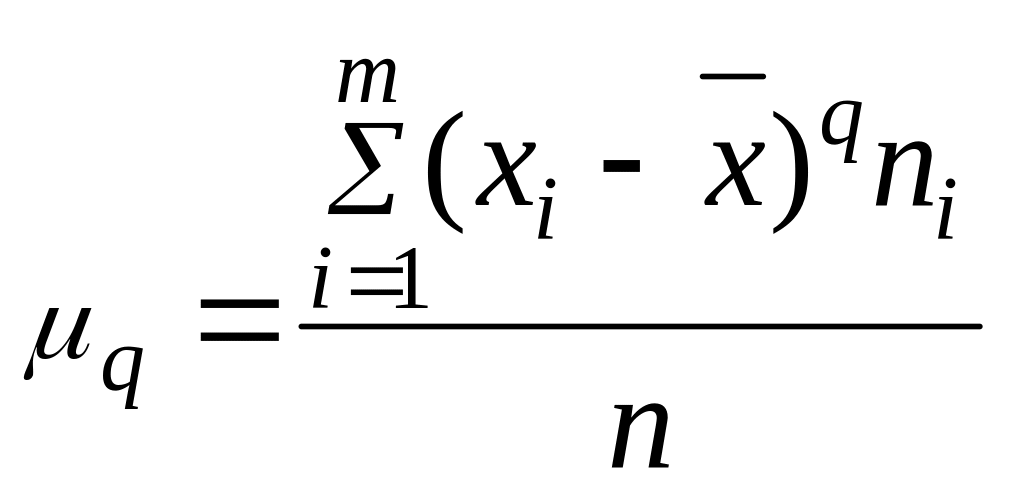

С помощью центральных моментов 3 и 4 рассчитывают коэффициенты асимметрии и эксцесс.

Коэффициент асимметрии показывает скошенность (асимметрию) данных: .

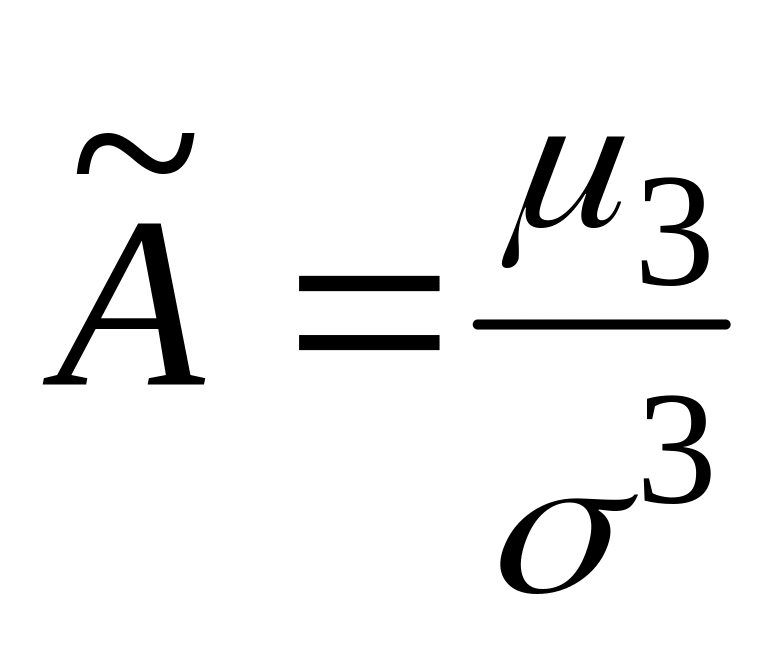Свойства коэффициента асимметрии: >0 ряд несимметричный с правосторонней асимметрией; <0 ряд несимметричный с правосторонней асимметрией; =0 ряд симметричный

В то время как показывает ассиметрии характеризуют симметричность распределения растет, показатели эксцесса показывают пиковость этого распределения

Свойства эксцесса: >0 распределение островершинное; <0 распределение плосковершинное; =0 распределение средневершинное соответствующее нормальное.

Величина Е|х|^k называется абсолютным моментом порядка k. Аналогично определяется момент совместного распределения случайных величин х₁, х₂, х₃,…х_n (так называемого многомерного распределения): для любых целых k_i>0, k₁ + k₂+…k_n=K, математическое ожидание Е( ) называется смешанным моментом порядка k, а Е(х₁ – Ех₁)^k1…(х_n-EX_n)^kn - центральным смешанным моментом порядка k. Смешанный момент Е(х₁-Ех₁)(х₂-Ех₂) называется ковариацией и служит одной из основанных характеристик зависимости между случайными величинами.

Если известны моменты распределения, то можно сделать некоторые утверждения о вероятностях отклонения случайной величины от ее математического ожидания в терминах неравенств. Наиболее известно неравенство Чебышева:

(1.4.5)

и его обобщения.

Задача, состоящая в определении распределения вероятностей последовательностью его моментов, носит название проблема моментов. В математической статистике для статистической оценки параметров распределения служат выборочные моменты.

Метод моментов является одним из распространенных общих методов получения статистической оценки. Заключается в приравнивании осредненного числа выборочных моментов соответствующим моментам исходного распределения, которые являются функциями от неизвестных параметров и решения полученных уравнений относительно этих параметров.