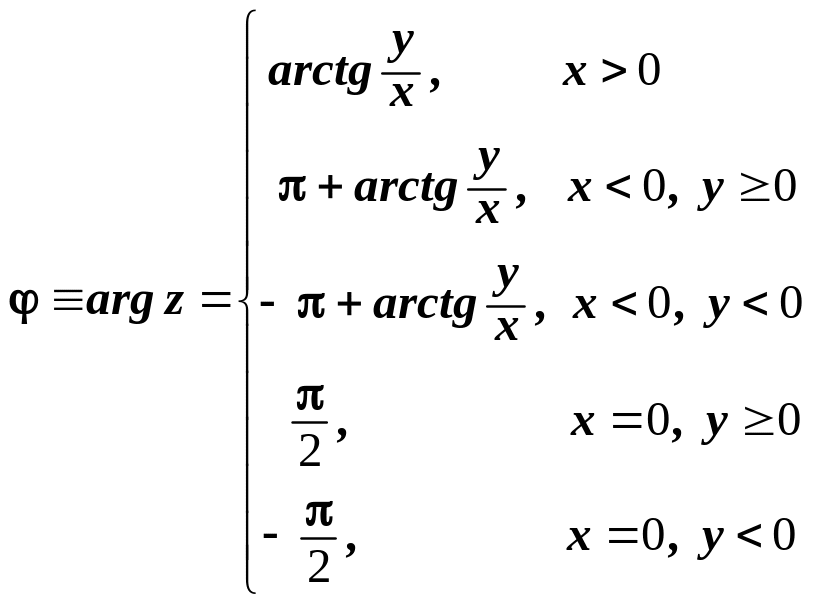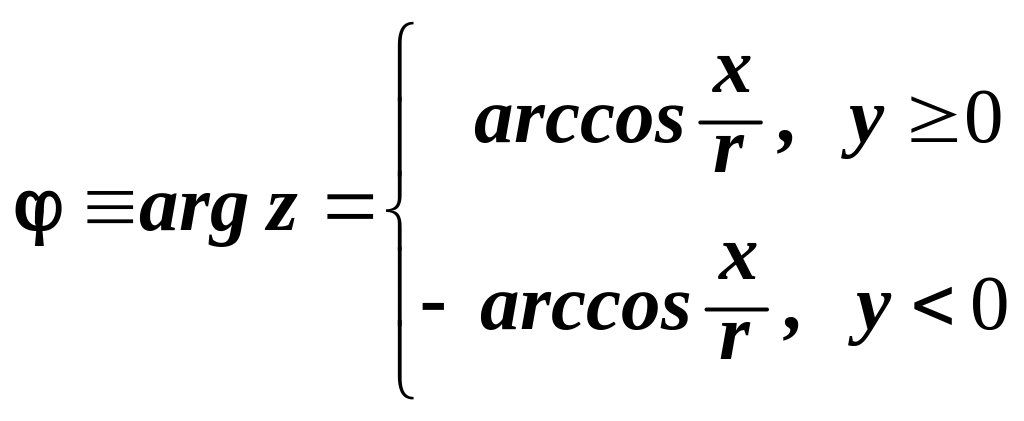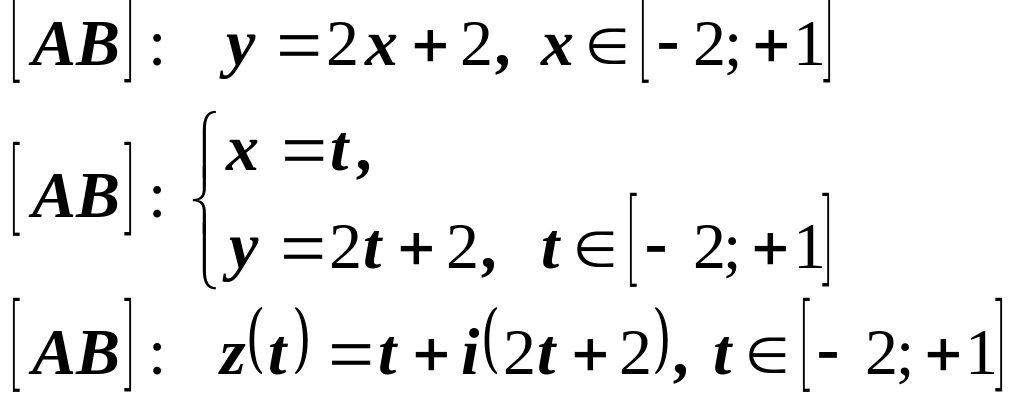К омплексні числа

Комплексні числа

Упорядкована пара (x, y) двох дійсних чисел x та y позначається z і називається комплексним числом (КЧ), якщо:

1) ;

2) .

Множина усіх комплексних чисел позначається С:

Дійсне число х є окремий випадок комплексного числа:

Комплексне число (0,1) називають уявною одиницею і позначають буквою i.

, де x — дійсна частина КЧ z (позн.: x = Re z від латин. realis – дійсний), y — уявна частина КЧ z (позн.: y = Jm z від латин. imaginarius – уявний ).

		Комплексне число z = (x, y) — це точка М(x, y). Вісь х-ів — це дійсна вісь; вісь y-ів — це уявна вісь.
	Комплексне число z — це вектор : — це модуль КЧ z, — це аргумент КЧ z, argz —це головне значення аргумента КЧ z ,

Координатна площина, на якій комплексні числа зображаються точками або векторами, називається комплексною площиною .

Поширена комплексна площина є поєднання комплексної площини з точкою .

Алгебраїчна форма комплексного числа z: z = x + iy
Визначення	Дії над КЧ
2) спряжене КЧ:	1) 2) 3) 4)

Формула Ейлера

Тригонометрична форма комплексного числа z:	Показникова форма комплексного числа z:
Формула Муавра: k = 0, 1, …, n – 1	Формула Муавра: , k = 0, 1, …, n – 1

Перехід від алгебраїчної форми кч

до показникової (або тригонометричної)

, , або

Приклади

Криві та області на комплексній

площині

Неперервна крива комплексної площини (z), що не має точок самоперетину, називається кривою Жордана (або простою кривою).

Параметричні рівняння кривої Жордана можна замінити одним комплексним рівнянням .

Якщо , то крива Жордана замкнена.

Коло — це жорданова крива

Лемніската Бернуллі —це не жорданова крива

Обхід замкненої жорданової кривої, здійснюваний таким чином, що її внутрішність залишається ліворуч, називається додатним.

Якщо крива незамкнена, то її додатний обхід відповідає зростанню параметра t.

Приклад

Рух по прямій від точки до точки вважається додатним, так як він відповідає зростанню параметра t.

Множина точок комплексної площини (z), що міститься всередині однієї замкненої жорданової кривої, називається однозв’язною областю.

Однозв’язна область D	Замкнена однозв’язна область

Двозв’язна область з границею	Тризв’язна область з границею

Будь-яку n – зв‘язну область можна перетворити в однозв’язну за допомогою -го перерізу так, як зображено на рисунку.

Приклад

Побудувати на площині

Елементарні трансцендентні функції

комплексної змінної та зв’язок між ними

Комплекснозначна функція визначає закон, за яким кожному значенню комплексної змінної з множини D відповідає одне, декілька або нескінченна множина значень комплексної змінної з деякої множини У першому випадку функція називається однозначною, у другому — багатозначною функцією комплексної змінної з областю визначення та множиною значень .

З геометричної точки зору: функція здійснює відображення множини точок комплексної площини на множину точок комплексної площини .

Однозначні функції
Визначення
1) 2) 3)	4) 5)
Формули, що пов’язують функції 1) — 5)

Періодичність однозначних функцій комплексної змінної

Багатозначні функції

1. Логарифмічна функція

(однозначна гілка: )

2. Загальна степенева функція

( — головне значення степеневої функції)

3. Загальна показникова функція

( — головне значення показникової функції)

4. Обернені тригонометричні функції

5. Обернені гіперболічні функції

Приклад. Обчислити

Використовуючи формулу , отримаємо

.

Приклад. Розв’язати рівняння .

Використовуючи формулу , отримаємо

,

.

Звідки

.

Остаточно

.

Диференціювання функції

комплексної змінної

Функція диференційовна в точці , якщо існує скінченна границя ( за будь-яким напрямком).