Лабораторна робота № 2 наближення функцій. Інтерполяція

1. Теорія

1.1 Постановка задачі чисельної інтерполяції

ДАНО:

На даному відрізку [а; b] відомі значення деякої функції в точках :

. (1.1)

Припускається, що всі точки різні і розташовані в порядку зростання.

ЗНАЙТИ:

Побудувати таку функцію , значення якої в точках співпадають із значеннями функції .

Функцію назвемо інтерполюючою функцією. Точки називаються вузлами інтерполяції.

РОЗВ'ЯЗАННЯ:

Шукатимемо інтерполюючу функцію у вигляді так званого інтерполяційного многочлена n-го степеня:

. (1.2)

Умова побудови запишеться так:

(1.3)

Доведено, що інтерполяційний многочлен існує і є єдиним. Тому коефіцієнти многочлена (1.2) знаходяться єдиним чином з умов (1.3).

В лабораторній роботі розглядатимуться різні форми подання інтерполяційного многочлена.

1.2 Інтерполяційний многочлен у формі Лагранжа. Схема Ейткена

Нехай функція задана умовами (1.1).

Інтерполяційним многочленом у формі Лагранжа називаєтся многочлен :

. (1.4)

Оцінка похибки формули Лагранжа: ,

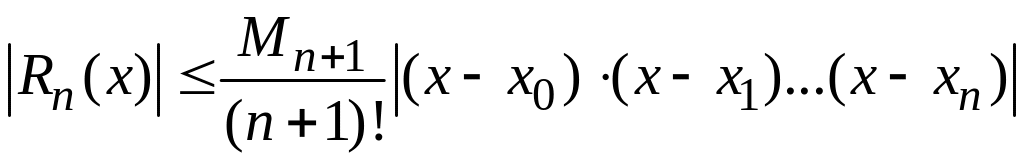де . (1.5)

Якщо потрібно обчислити не загальний вираз , а лише його значення при конкретному , і при цьому значення функції дані в достатній кількості вузлів, то можна використати інтерполяційну схему Ейткена.

Згідно з цією схемою послідовно обчислюються многочлени:

,

,

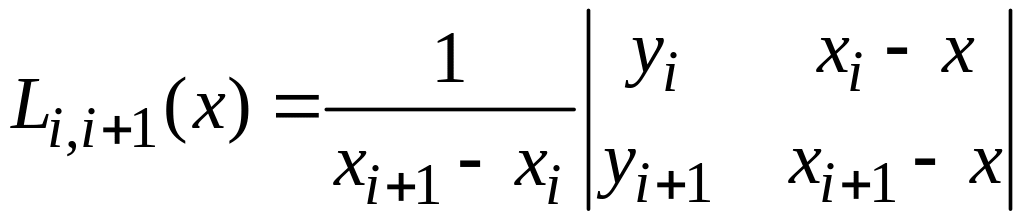і т.д.

Інтерполяційний многочлен -го степеня, який приймає в точках значення ( ), запишеться так:

.

Обчислення за схемою Ейткена зручно розташувати в таблиці (табл. 1.1).

Таблиця 1.1 - Інтерполяційна схема Ейткена

Обчислення за схемою Эйткена зазвичай ведуть до тих пір, поки послідовні значення і не співпадуть в межах заданої точності. Схема Ейткена легко реалізується на ЕОМ і забезпечує можливість автоматичного контролю точності обчислень.

Приклад 1.1 Функція задана таблицею:

	1.0	1.1	1.3	1.5	1.6
	1.000	1.032	1.091	1.145	1.170

Застосувавши схему Ейткена, знайти .

Розв'язок.

Записуємо ці значення функції в табл. 1.2. і обчислюємо різниці при .

Таблиця 1.2 - Схема Ейткена для прикладу 1.1

0 1 2 3 4	1,0 1,1 1,3 1,5 1,6	1,000 1,032 1,091 1,145 1.170	-0,15 -0,05 0,15 0,35 0,45	1,048 1,047 1,050 1,057	1,048

Потім послідовно знаходимо:

Отримані значення L_i-1 заносимо в таблицю, після чого обчислюємо

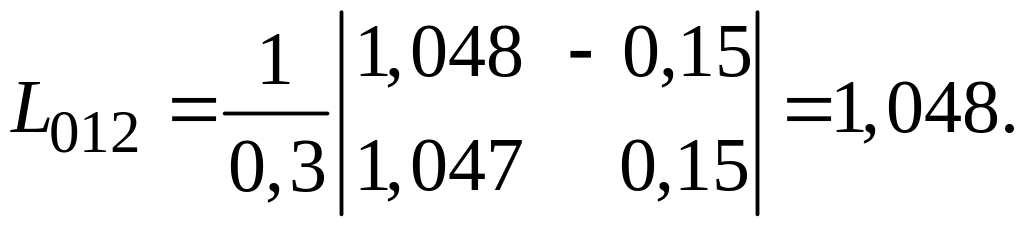
Значення і співпадають до третього знаку. На цьому обчислення можна припинити і з точністю до 10^-3 записати