Лекция №9.

Необходимо вычислить q_i. Время выборки команды из ОП является случайной величиной, подчиняющейся произвольной функции распределения F(t). Пусть время выборки одной команды равно t. Разобьем это время на m одинаковых интервалов по t (t*m=t). Вероятность того, что за время t будет выполнена ровно одна команда в условиях экспоненциального закона распределения, равна: . Вероятность того, что за время t выполнится ровно i команд, равна:

Экспоненциальный закон распределения для случая «нелинейной» программы.

Рассмотрим команду условного перехода (УП), результатом ее выполнения может быть либо выполнение команды с меткой, указанной в команде УП, либо выполнение следующей (по написанию) команды за командой УП. Так как же быть в данной ситуации? Пусть мы в БП заносим следующие команды за командой УП, тогда только после выполнения команды УП будет ясно угадано направление или нет, если не угадано, то необходимо аннулировать все команды, которые были занесены в БП, и изменить АО. Опишем эту модель математически: любая команда, которая выполняется в ЦП, является с некоторой вероятностью командой перехода, а с дополнительной вероятностью - командой следования. Если в настоящее время выполняется команда условного перехода, то с некоторой вероятностью она не меняет порядок выполнения команд и с дополнительной - меняет, следовательно вероятность того, что надо будет уничтожать команды, находящиеся в БП, после выполнения одной из команд равна произведению вероятности того, что текущая команда является командой условного перехода, и вероятности того, что она изменит порядок выполнения команд. Обозначим ее через .

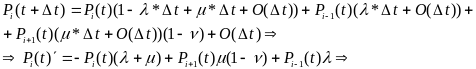
Для стационарного случая:

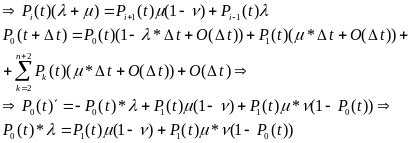
ДЗ. Р_n+2(t)-?

Модель конвеерной обработки.

Средняя задержка команды на входе равна средней задержке команды на входе. Среднюю задержку (латентность) мы находим из графа переходов конвейера. Найдем нижнюю (L_min) и верхнюю (L_max) границу средней латентности (L).

Теорема: L_minLL_max, где L_max - число единиц в начальном векторе столкновений, а L_min находится из таблицы занятости - подсчитывается число меток в каждой строке и выбирается максимальное число.

Доказательство:

1. L_minL. Пусть L - средняя латентность, тогда r=1/L - темп поступления или выдачи команд (количество инициаций). Введем к_i - коэффициент использования i ступени. Пусть d_i-число меток в i-ой строке. Оно характеризует, как использовать i-ый сегмент. 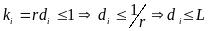будем считать, что это неравенство действует для любого числа i, т.е. 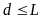, где

2. LL_max. Докажем это утверждения для случая, когда граф состояний представляет собой простой, замкнутый цикл (простой цикл - это цикл в котором любое из состояний не повторяется). Докажем, что для такого цикла (жадная стратегия) L_max = числу единиц в начальном векторе столкновения. Рассмотрим модифицированный граф (только инициации). Обозначим за L₁ задержку при переходе от S₁ к S₂. L₁ - число единиц до первого нуля. В каждом состоянии существует свой вектор столкновения (S_i). Обозначим за L₁ задержку при переходе от S₁ к S₂. L₁ - число единиц до первого нуля. S₂ получается путем сдвига S₁ на L₁ позиций и прибавлением к нему начального вектора столкновений. Пусть x_i - число единиц в векторе столкновения, отвечающему i-ому состоянию. х - число единиц в начальном векторе столкновений.

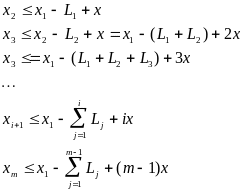
Замкнем круг

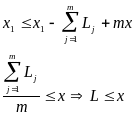
Что и требовалось доказать.