- •Лекция №1. Введение.
- •Моделирование бп типа кэш.
- •Структурированный подход.
- •Лекция №2 Оценка вероятности промаха бп типа кэш.
- •Лекция №3 Секторное отображение.
- •Оптимальный алгоритм замещения.
- •Лекция №5. Опережающая обработка информации.
- •Дискретное распределение.
- •Лекция №6. Геометрическое распределение.
- •Лекция №7. Экспоненциальное распределение.
- •Лекция №8
- •Вложенные цепи Маркова. Произвольная функция распределения.
- •Лекция №9.
- •Экспоненциальный закон распределения для случая «нелинейной» программы.
- •Модель конвеерной обработки.
Лекция №6. Геометрическое распределение.
Системы (*) и (**) (см. прошлую лекцию) определяют функцию распределения времени выполнения команды в устройстве. В этом случае граф переходов будет очень сложным и определить в явном виде вероятности простоя сложно. Если мы зададим функцию распределения более упрощенно, то мы продвинемся в решении задачи. В связи с выше сказанным введем для описания времени выполнения команды в устройстве геометрический закон распределения.
Геометрическое распределение характеризуется двумя параметрами периодом () и вероятностью () повторения данного периода.
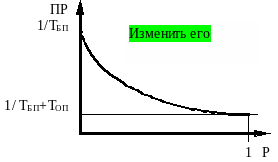
Пример.
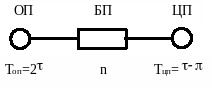
Построим граф переходов данной системы.
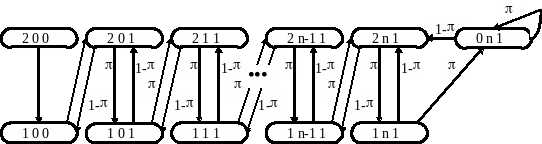
Составим систему уравнений
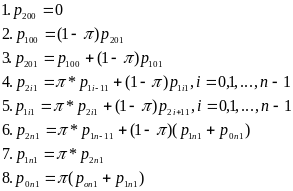
В данной системе одно уравнение линейно зависимо, следовательно надо отбросить любое уравнение и добавить уравнение нормировки. Решается эта система любым из известных способов.
![]()
Найдем
![]() цп
цп
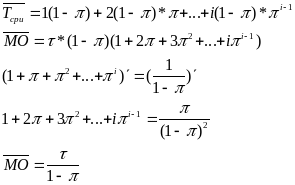
Лекция №7. Экспоненциальное распределение.
Экспоненциальное распределение является непрерывным распределением и является приближением геометрического распределения, т.к. при стремлении такта к 0 геометрическое распределение стремиться к экспоненциальному.
Определение:![]() -
вероятность того, что выполнение команды
завершится к моменту времени t.
-
вероятность того, что выполнение команды
завершится к моменту времени t.
Для экспоненциального закона распределения
![]() .
.
F(t)
1
t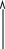
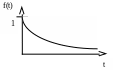


Дополнении к функции распределения:![]() - вероятность того, что выполнении
команды не закончиться к моменту t.
- вероятность того, что выполнении
команды не закончиться к моменту t.
Плотность вероятности:![]()
ДЗ. Просмотреть свойства экспоненциального закона распределения. Математическое ожидание, дисперсия, первый и второй моменты.
Рассмотрим такую модель:
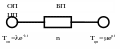
Поскольку время выполнения команды не зависит от того сколько данная команда выполнялась до этого нет необходимости вводить параметр, который будет содержать информацию о том сколько времени уже выполняется команда в процессоре, или в памяти, или одновременно и там и там, следовательно достаточно указать сколько находиться команд в системе (от 0 до n+1). Рассмотрим состоянии системы в некоторый момент времени t. Введем Рi(t) - вероятность того, что в момент наблюдения t в системе находится ровно i команд. При i=0,1,...,n+1 ОП не может быть заблокировано. Введем n+2 состояние и будем считать, что в этом состоянии ОП заблокировано.
Найдем Рi(t). Для этого рассмотрим малый интервал времени t и пусть в момент t+t система находиться в состоянии i. Найдем вероятность Pi(t+t) для всех значениях i. В момент времени t система могла находиться в любом состоянии. Посмотрим как можно из состояния системы в момент времени t попасть в состояние i в момент времени t+t.
0<i<n+2
![]() вероятность
того, что ни ОП, ни ЦП не завершит обработку
команды или оба устройства выполнят
одно и тоже число команд.
вероятность
того, что ни ОП, ни ЦП не завершит обработку
команды или оба устройства выполнят
одно и тоже число команд.
Определим вероятность того, что за t ни ОП, ни ЦП не завершит обработку команды:
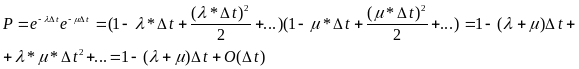 ДЗ.
Разложение ех.
ДЗ.
Разложение ех.
Символ О(t) означает величины, для которых справедливо O(t )/ t 0 при t. Вероятность того, что за t устройствами будет выполнено ровно по к команд равняется О(t).
Действительно:![]() .
.
Поэтому:
![]()
![]()
![]() +
+![]() вероятность
того, что за время t
1) ЦП выполнит 1 команду, а ОП - 0 команд,
либо 2) ЦП выполнит на 1 команду больше
чем ОП.
вероятность
того, что за время t
1) ЦП выполнит 1 команду, а ОП - 0 команд,
либо 2) ЦП выполнит на 1 команду больше
чем ОП.
Определим вероятность первого события:
![]() .
.
Вероятность второго события равна О(t). Следовательно:
![]() +
+
![]()
![]()
![]()
![]() вероятность
того, что 1) ЦП выполнит 2 команды, а ОП
ни одной, либо 2) ЦП выполнит на 2 команды
больше, чем в ОП.
вероятность
того, что 1) ЦП выполнит 2 команды, а ОП
ни одной, либо 2) ЦП выполнит на 2 команды
больше, чем в ОП.
Определим вероятность первого события:
![]() .
.
Вероятность второго события равна О(t). Отсюда вероятность попадания в состояние i из состояния i+2 равна О(t), аналогично и из состояния i-2. Следовательно и из состояний i3, i4,...,ik вероятность попадания в состояние i равна О(t).
Мы получили формулу полной вероятности того, что система окажется в момент времени t+t в состоянии i (0<i<n+2):
![]() +
+
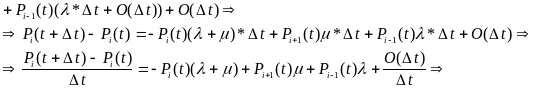
( возьмем предел каждой части равенства
при t)
![]()