Лекция №3 Секторное отображение.
Пусть V-объем БП, S-число секторов. Алгоритм замещения LRU.
ДЗ. Доказать, что для FIFO будет аналогично.
Оптимальный алгоритм замещения.
Рабочая нагрузка состоит из операторов следования и цикла. l - длина программы. V - объем БП. Рассмотрим чисто ассоциативное отображение (S=V).
Какие блоки останутся в БП после 1-го цикла ?
1 2 . . . S-1 S
Дальше в БП надо поместить S+1 блок. Мы будем вытеснять S -ое место БП и ставить последующие блоки на это место, то есть остаются не вытесненными те блоки, которые понадобятся в недалеком будущем.
1 2 . . . S-1 S+1
1 2 . . . S-1 S+2
..........................
1 2 . . . S-1 L
В первом цикле произошло L промахов.
2-ой цикл. До S-1 блока промахов нет. Дальше надо вытеснять c S-1-ого места
1 2 . . . S-2 S L
1 2 . . . S-2 S+1 L
............................
1 2 . . . S-2 L-1 L
Во втором цикле произошло (L-2)-(S-1)+1=L-S промахов
3-ий цикл.
1 2 . . . S-3 S-1 L-1 L
1 2 . . . S-3 S L-1 L
...................................
1 2 . . . S-3 L-2 L-1 L
L-S промахов
S-ый цикл
...................................
L-S+1 L-S+2 . . . L-1 L
S+1-ый цикл.
1 L-S+1 L-S+2 . . . L-1
2 L-S+1 L-S+2 . . . L-1
.......................................
L-S L-S+1 L-S+2 . . . L-1
L-S L-S+1 L-S+2 . . . L-2 L
L-S+1 промахов
S+2 цикл
1 L-S . . . L-2
.......................
L-S-1 L-S . . . L-2
L-S-1 . . . L-3 L-1
L-S-1 . . . L-3 L
S+3 цикл
1 L-S-1 . . . L-3
.........................
L-S-2 L-S-1 . . . L-3
L-S-2 . . . L-4 L-2
L-1
L
В конце концов будет
1 2 . . . S-1 L
Построим зависимость числа промахов от числа циклов
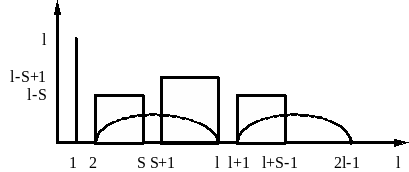
Пр. Пусть L=44 T=5 S=8 Найти вероятность промаха
число промахов: 44+36*4
ДЗ. Найти вероятность промаха для чисто ассоциативного отображения для произвольного Т.
Оптимальный алгоритм замещения для группо-ассоциативного
отображения.
РИСУНОК
ДЗ. Найти вероятность промаха для группо-ассоциативного отображения для произвольного Т.
Лекция №4.
Моделирование алгоритмов замещения при задании рабочей нагрузки посредством Марковской модели.
Пусть имеется n блоков в
БП. Введем независимую модель. Она
задается вероятностью (
)
обращения к i-ому
блоку. Зависимая (марковская) модель
задается
-
вероятность того, что предыдущее
обращение было к i-ому
блоку, а текущее к j-ому.
Такое задание адресной трассы является
приближенным. Истинная адресная трасса
задается вероятностью, зависящей от
всех предыдущих обращений.
Алгоритм замещения LRU.
Пусть БП имеет чисто ассоциативное отображение, следовательно имеется V=S мест. Для того чтобы описать состояние БП типа кэш необходимо использовать вектор длиной S, и элементы этого вектора есть номера блоков, которые находятся в кэш. Пусть блоки в векторе располагаются по принципу: слева - самый «молодой», а справа - самый «старый».
Например пусть для S=4 вектор будет 5,3,7,8. Тогда самый «молодой» будет блок с номером 5, а самый «старый» - 8.
-
вероятность того, что вектор,
описывающий состояние БП, будет
Пусть S=2, n=3. Построим граф переходных вероятностей, у которого число состояний - это число размещений n по S.
P11
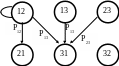
ДЗ. Достроить граф.
Найдем вероятность
для этого нужно рассмотреть дуги,
входящие в 1,2, и расписать каждое
обращение-состояние.
А вероятность промаха будет:
В общем случае
(*)
ДЗ. S=3, n=6. Найти
.
Мы имеем систему
уравнений типа (*), но одно из них линейно
зависимо. Его отбросим и добавим условие
нормировки :
Выразим из системы все
и подставим в выражение вероятности
промаха:
Двоичное дерево.
Пусть n-произвольное, S=8.
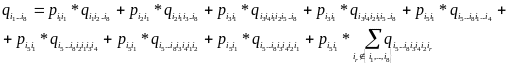
ДЗ. 1) S=8,n=12.
-?
2) Построить граф переходов для а) равновероятного алгоритма замещения;
б) алгоритма замещения FIFO.