2.2. Методика расчета интегрального пав-фильтра

На кафедре радиоприемных устройств разработан пакет прикладных программ для расчета радиоприемного устройства дискретной системы связи. В состав пакета входит программа "Расчет полосно-избирательного фильтра на ПАВ", структурная схема которой представлена на рис.2.10. На примере работы этой программы рассмотрим порядок расчета интегрального пьезофильтра на ПАВ.

Исходными данными для расчета фильтра являются:

1) промежуточная частота f₀, МГЦ;

2) полоса пропускания фильтра fп, МГц;

3) допустимая неравномерность в полосе

пропускания A, дБ;

4. минимальное ослабление в полосе задерживания

В,дБ;

4. крутизна склона нормированной АЧХ К.

Ввод исходных данных осуществляется с клавиатуры дисплея (оператор 2).

Допустимая неравномерность А амплитудно-частотной характеристики представляется в виде суммы трех составляющих:

А = А1+А2+А3

где А1 - неравномерность АЧХ при использовании модели возбуж­дения (приема) ПАВ δ-источниками (приемниками);

A2 - неравномерность АЧХ за счет сигнала трехкратного прохождения;

А3 - неравномерность АЧХ за счет электромагнитных наводок между ВДП.

При данном представлении неравномерности АЧХ из вторичных эффектов, искажающих частотную характеристику, учитываются только сигнал трехкратного прохождения и электромагнитные наводки. В отношении остальных эффектов считается, что их влияние пренебрежимо мало благодаря соответствующим мерам[11].

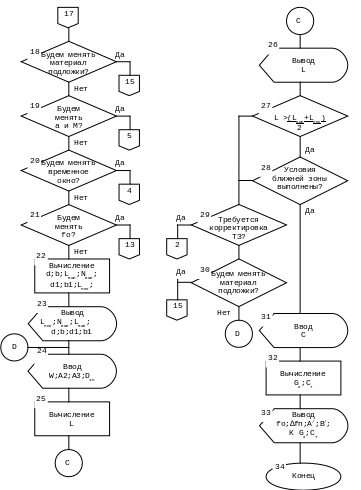
Рис.2.10 Структурная схема программы расчета полосно-избирательного фильтра на ПАВ

Выбop значений A1,А2,А3 в значительной степени компромиссный. При уменьшении А1 увеличивается число электродов ВШП и уменьшается минимальное перекрытие электродов, что затрудняет борьбу с дифракционными искажениями. Значение А1 не должно быть меньше 0,2..0,3 дБ. При уменьшении А2 возрастает вносимое фильтром затухание из-за необходимости более сильно­го подавления сигнала трехкратного прохождения. Согласно табл.2.1 не следует выбирать А2<0,07...0,2 дБ. При уменьшении А3 необходимо увеличивать расстояние между входным и выходным ВШП, что увеличивает размеры фильтра и затрудняет борьбу с дифракционными искажениями и наводками. Минимальное значение А3 равна O,1...0,2 дБ.

После ввода в ЭВМ выбранных значений величин А1,А2,А3 (оператор 3) приступают к непосредственному синтезу фильтра. Как отмечалось выше, полосно-избирательный фильтр целесообразно отроить на двух одинаковых ВШП, полагая H_BX(f)=H_вых(f)=H(f), где H(f) - некоторая частотная характеристика, модуль которой |H(f)| имеет близкую к П-образной форму. При этом частотная характеристика фильтра

поэтому АЧХ |Н_ф(f)|=|H(f)|² близка к П-образной, а ФЧХ оказывается линейной.

Таблица 2.1

Влияние сигнала трехкратного прохождения на

частотную характеристику фильтра.

Уровень сигнала трехкратного прохождения, дБ	Неравно- мерность		Уровень сигнала трехкратного прохождения, дБ	Неравно-мерность
	АЧХ, дБ	ФЧХ, φо		АЧХ, дБ	ФЧХ, φо
-12	4,459	28,2	-32	0,436	2,9
-16	2,777	18,0	-36	0,276	1,8
-20	1,740	11,4	-40	0,173	1,1
-24	1,097	7,2	-44	0,110	0,72
-28	0,692	4,6	-48	0,070	0,46

Известно, что идеальную прямоугольную фору частотной характеристики

где - полоса пропускания, физически нельзя реализовать, так как импульсная характеристика

в этом случае бесконечна во времени. Усечение h(t) во временной области на интервале [-Т, Т] приводит к появлению в H(f) краевых пульсаций (эффект Гиббса), уменьшает крутизну склона |H(f)| и увеличивает полосу пропускания ∆f_п (рис.2.11). Увеличение длительности интервала усечения увеличивает крутизну склона |H(f)|, но мало сказывается на неравномерности А и затухании В. Применение временного взвешивания, которое заключает­ся в умножении импульсной характеристики фильтра на некоторую симметричную плавно спадающую к краям интервала [Т, Т] временную функцию окна, позволяет уменьшить пульсации частотной характеристики

Рис. 2.11 Влияние усечения импульсной характеристики на частотную характеристику фильтра

Некоторые виды функций временного окна приведены в таблице 2.2 (функции временного окна определены на интервале [-Т, Т] и за пределами этого интервала обращаются в нуль, поэтому импульсные характеристики ВШП, соответствующие своим функциям временного окна, определены при |t|≤T и при |t|>T тождественно равны нулю; приведенные в табл. 2.2 выражения для функции временного окна и импульсной характеристики ВШП соответствуют |t|≤T).

При расчете частотной характеристики ВШП полосно-избирательный фильтр с импульсной характеристикой h(t) заменяется низкочастотным аналоговым фильтром-прототипом с импульсной характеристикой h_нч(t) (для прямоугольного окна, например, ).Частотные характеристики этих фильтров связаны равенством

Н(f_o+F)=H_нч(F)

где F=f-f_o - разностная частота [11]. Однако для некоторых типов весовых функций (как, например, для окна Кайзера) частотную характеристику ВШП невозможно получить аналитически. Поэтому используется численный метод расчета H_нч(F) на ЭВМ с помощью программы быстрого преобразования Фурье (БПФ). Для этого низкочастотный аналоговый фильтр-прототип заменяется дискретно-аналоговым фильтром с импульсной характеристикой

Таблица 2.2

Некоторые типы весовых функций

Временное окно	Функция временного окна	Импульсная характеристика ВШП
Прямо-угольное	1
Фейера	1-|at/Т|
Каппелини
Хэннинга
Хэмминга
Блэкмана
Гаусса
Кайзера

Например, в случае пользования прямоугольного окна . Для уменьшения ошибки вычислений за счет эф­фекта "наложения" шаг дискретизации τ выбирается небольшим, меньше предела 1/∆f, устанавливаемого теоремой Котельникова. При шаге

τ =1/4 ∆f

эффект "наложения" можно не учитывать и полагать

H_нч(F)=H(F)

на интервале [-∆f, ∆f], где H(F)- частотная характеристика дискретно-аналогового фильтра. Число отсчетов импульсной характеристики

2М =8∆fТ

Так как в программе используется БПФ по основанию 2, то число отсчетов импульсной характеристики выбирается

N_БПФ=2^τ

где t - целое число, причем N_БПФ≥2М, а недостающие отсчеты импульсной характеристики представляются нулями. Частотная ха­рактеристика ВШП вычисляется в дискретных точках

H(m∆F)=H(F)|_F=m∆F

причем шаг ∆f на частотной оси определяется N_БПФ:

∆F =4∆f/ N_{БПФ .}

Поэтому, чем больше размер БПФ, тем точнее рассчитывается H(m∆F).

Следует отметить, что поскольку функции временного окна являются симметричными, то частотная характеристика H(m∆F) принимает только вещественные значения. Поэтому амплитудно-частотная характеристика |H(m∆F)| совпадает с H(m∆F) при H(m∆F)≥0, а фазочаcтотная характеристика аrgН(m∆F)=0 –при всех значениях m∆F.

Для расчетов удобно пользоваться обобщенной расстройкой

ξ=2m∆F/∆f

и нормированной частотной характеристикой

Ho(ξ)= H(ξ)/H(ξ=0)

При ∆F=4∆f/N_БПФ обобщенная расстройка ξ=8m/N_{БПФ .}

При одинаковых ВШП неравномерность А в полосе пропускания, ослабление В в полосе задерживания и крутизна склона К частотной характеристики фильтра распределяются поровну между входным и выходным ВШП. Поэтому считается, что для отдельного ВШП выполняются следующие условия:

(2.3)

Эта информация выводится на экран в процессе ввода исходных данных (после оператора 3), является вспомогательной и на рис.2.10 отдельным оператором не представлена.

Параметры a (см.табл.2.2) и М выступают в роли изменяемых параметров фильтра, подбором которых можно обеспечить заданные требования (2.3) к частотной характеристике. Так, увеличение параметра а приводит к уменьшению неравномерности частотной характеристики в полосе пропускания и увеличению затухания в полосе задерживания, а увеличение параметра М приводит к более прямоугольной форме частотной характеристики, т.е. увеличивается крутизна склона АЧХ (более подробно с влиянием параметров а и М на ход АЧХ при использовании окна Кайзера можно ознакомиться в [11]). Однако следует иметь в виду, что с увеличением этих параметров сложнее подавлять вторичные эффекты, искажающие частотную характеристику фильтра.

Кроме того, при увеличении а и М растут габариты фильтра. Поэтому необходимо стремиться к минимальным значениям а и М, обеспечивающим условие (2.3). Следует также помнить, что параметр М принимает только целочисленные значения. При выборе начальных значений а и М для окна Кайзера можно воспользоваться графиком, приведенным в [11].

После выбора весовой функции (оператор 4) и ввода параметров а и М (оператор 5) рассчитывается нормированная частотная характеристика ВШП Ho(ξ) и по ней определяется значение нера­вномерности в полосе пропускания А_ВШП, ослабление в полосе за­держивания В_ВШП и крутизна склона К_ВШП отдельного ВШП (опера­тор 6). Рассчитанные значения А_ВШП, В_ВШП и К_ВШП выводятся на экран дисплея (оператор 7).

Если полученные значения А_ВШП, В_ВШП и К_ВШП не удовлетворяют условиям (2.3), то следует изменить параметры а и М и повторить расчет (оператор 8) или перейти к другому виду временного окна (оператор 9). Если после многократных расчетов так и не удается обеспечить требования (2.3), то можно скор­ректировать значение неравномерности в полосе пропускания А1 (оператор 10) и снова повторить расчеты. Следует помнить о том, что если появится необходимость вернуться к старым значениям а и М, введенным в ЭВМ при первых попытках обеспечить требования (2.3), то необходимо повторить ввод этих значений (операторы 4, 5) и заново рассчитать частотную характеристику, так как в машине с целью экономии памяти сохраняются только текущие значения параметров а и М и соответствующий им вариант расчета частотной характеристики ВШП.

В процессе вычислений А_ВШП, В_ВШП и К_ВШП и удовлетворения требований (2.3) определяются необходимые параметры а и М. Определив их, можно конкретизировать вид функции аподизации с точностью до параметра ∆f/f. Функция аподизации может быть получена из выражения для импульсной характеристики ВШП

(см табл.2.2) при подстановке t=кd/V_a, где к-номер электрода, d-шаг между электродами, V_a-скорость ПАВ. Замечая, что при резонансной частоте fo, шаг d=V_a/2fo , и выражая Т из равенства M=4∆fT, получаем функцию аподизации ВШП. В табл.2.3 сведены функции аподизации ВШП для различных временных окон. Значение параметра ∆f/fo уточняется позже исходя из заданной полосы ∆fп пропускания фильтра.

Отметим, что при идеальной П-образной частотной характеристике фильтра ∆f=∆f_п. В реальных фильтрах ∆f>∆fп (см.рис.2.11).

По нормированной частотной характеристике ВШП рассчитывают характеристику избирательности в децибелах:

L_ВШП(ξ)=-20lg|Ho(ξ)| ,

по которой определяется значение ξп обобщенной расстройки, соответствующее границе полосы пропускания фильтра (оператор 11). Значение ξп равно такой обобщенной расстройке, при которой ослабление на склоне характеристики избирательности оказывается равным 0,5 А_ВШП (рис.2.12). При данном определении ξп неравномерность АЧХ в пределах полосы пропускания

Таблица 2.3

Функции аподизации ВШП и минимальное значение модуля функции аподизации для различных типов весовых функций

Временное окно	Функция аподизации ВШП ω(к)	|ωmin|
Прямо- угольное
Фейера
Каппелини
Хэннинга
Хэмминга
Блэкмана
Гаусса
Кайзера

фильтра (с учетом двух ВШП) окажется равной 2А_ВШП и согласно (2.3) не превзойдет допустимого значения А1.

Нормированная частотная характеристика ВШП Ho(ξ), харак­теристика избирательности ВШП L_ВШП(ξ) и значение ξп выводятся на экран дисплея (оператор 12).

Для того чтобы фильтр имел заданную полосу ∆fп пропускания, необходимо еще найти соответствующе значение параметра ∆f/fо функции аподизации.

Рис.2.12. Определение обобщенной расстройки

Замечая, что ξ =1 отвечает раcстройка ∆f/2, а ξ=ξп -расстройка ∆fn/2, находим ∆f=∆fn/ξп. Таким образом, заданная полоса пропускания обеспечивается при выборе ∆f/fо=∆fп/(ξоfo)(оператор 13). Значение параметра ∆f/fо также выводится на экран дисплея (оператop 14).

На этом завершается синтез фильтра, так как оказываются oпределенными все три его параметра: ∆f/fо, М и а.

На следующем этапе выбирается материал для пьезоэлектрической подложки и определяются геометрические размеры фильтра исходя из допустимого уровня искажений частотной характеристики за счет дифракции ПАВ и электромагнитных наводок между входным и выходным ВШП.

По табл.2.4 определяется и вводятся в ЭВМ значения скорости ПАВ V_a, коэффициента анизотропии и коэффициента электромеханической связи R² (оператор 15) предполагаемого материала пьезоподложки. В табл.2.4 кварцу 1 соответствует пьезокварц Y-среза с направлением X распространения волны, кварцу 2- пьезокварц среза- 20°Y с направлением X распространения волны, кварцу 3- пьезокварц среза + 42,75°Y с направлением X распространения волны. Ниобат и танталат лития имеют Y-срезы и направление Z распространения волны.

При выборе материала для пьезоподложки следует в первую очередь руководствоваться допустимым уровнем дифракционных искажений частотной характеристики.

Таблица 2.4

Физические свойства

пьезоэлектрических монокристаллов

Материал пьезо-подложки	Коэффициент электро-механической связи k2	Погонная емкость пары электродов С, пФ/см	Скорость ПАВ*105, см/с	Коэффи-циент анизо-тропии
Кварц 1	0,23	0,55	3,159	1,65
Кварц 2	0,25	0,55	3,209	1,45
Кварц 3	0,16	0,55	3,157	1,38
Ниобат лития	4,50	4,50	3,488	0,083
Танталат лития	0,74	5,70	3,230	0,79

В [11] отмечено, что дифракционные искажения незначительны, если ширина W апертуры звукопровода удовлетворяют неравенству

где λ_a -длина волны ПАВ; γ -коэффициент анизотропии пьезоподложки; N_ВШП -число промежутков между электродами ВШП; |ω_min| -минимальное значение модуля функции аподизации. Из этого неравенства нетрудно установить, что при выборе материала для пьезоподложки необходимо учитывать соотношение

(2.4)

Значение |ω_min| нетрудно определить, зная функцию аподизации ВШП (в табл.2.3 приведены выражения для |ω_min| при различных функциях временных окон). Число промежутков между электродами ВШП можно определить по формуле

N_ВШП =M/(∆f/fo)

Таким образом, вычисляя |ω_min| и N_ВШП для предполагаемого материала пьезоподложки, можно определить минимальное значение ширины апертуры фильтра W_min. Максимальное значение ширины апертуры фильтра ограничивается технологией изготовления кристалла для пьезоподложки, габаритами фильтра и обычно не превышает 20-30 мм. Для уменьшения габаритов фильтра целесообразно выбирать апертуру W минимально возможной.

Рассчитанные значения W_min и W_ВШП (оператор 16) выводятся на экран дисплея (оператор 17). Вслед за этим на экран дисплея выводятся значения:

- промежуточной частоты fo, МГц;

- параметров фильтра а и M;

- слагаемых допустимой неравномерности в полосе

пропускания A1, A2 и А3, дБ;

- коэффициента анизотропии материала

пьезоподложки γ.

Эта справочная информация необходима для того, чтобы помнить, какими значениями перечисленных параметров оперирует ЭВМ в данный момент, так как при длительных расчетах оператор может неоднократно изменять эти значения в ходе вычислении геометрических размеров фильтра. На структурной схеме рис.2.10 справочная информация отдельным оператором не представлена.

Если неравенство(2.4)не выполняется ни при одном материале пьезоподложки, который можно заменить в ходе вычислений (оператор 18), то необходимо пересчитать фильтр для меньших значений М и а (оператор 19) или для другого типа временного окна (оператор 20). В тех случаях, когда неравенство (2.4) не выполняется, но левая и правая его части имеют близ­кие значения, можно несколько увеличить промежуточную частоту fo и за счет этого выполнить данное неравенство (оператор 21).

Для аподизованных фильтров наиболее подходящим материалом пьезоподложки оказывается ниобат лития Y-среза, в котором акустическая энергия имеет тенденцию к распространению вдоль оси Z. Ниобат лития имеет минимальный коэффициент анизотропии.

После выбора материала пьезоподложки определяются размеры ВШП- ширина апертуры W и длина L_ВШП. Ширина апертуры уже была установлена при выборе материала, длина ВШП

L_ВШП=0,5λ_эN_ВШП

Расчет геометрических размеров МПО сводится к определению его длины L_МПО, так как ширина МПО определяется шириной апертуры входного и выходного ВШП. Число электродов МПО определяется по формуле [9]:

N_МПО=λ_э/(k₂d₁)

где λ_э- длина акустической волны в звукопроводе, k₂- коэффициент электромеханической связи, d₁- пространственный шаг электродов МПО. Коэффициент электромеханической связи (см.табл.2.4) характеризует эффективность взаимодействия ПАВ с проводящими электродами. В случае d₁=0,75d, где d=0,5λ_э- пространственный шаг электродов ВШП.

N_МПО=8/(3k²)

При этом длина МПО

L_МПО=0,375λ_э(N_МПО-1)

Рассчитанные значения L_МПО, N_МПО, L_ВШП, d, b, d₁ и b₁ (оператор 22) выводятся на экран дисплея (оператор 23).

Осталось еще установить расстояние L между центрами ВШП. От этого расстояния зависит электромагнитная развязка D_эм между входным и выходным ВШП. Расстояние L находится по формуле [4]:

L=WD_эм/(22,25)

где развязка D_эм задана в децибелах. Значение W , выбранное в соответствии с выведенным ранее значением W_min и значение D_эм, найденное по табл. 2.1 в соответствии с выбранным значением допустимой неравномерности А₃ частотной характеристики за счет электромагнитных наводок между ВШП, вводятся в ЭВМ с пульта дисплея (оператор 24). Вычисленное значение L (оператор 25) выводится на экран дисплея (оператор 26).

При вычислении L необходимо следить за тем. чтобы выполнялось условие (оператор 27)

L>(L_ВШП+L_МПО)/2 (2.5)

При выполнении неравенства (2.5) остается убедиться в том, что дифракционные искажения незначительны, т.е. необходимо прове­рить условие ближней зоны (оператор 28)

|ω_min|² W²/(γλ_эL)>1 (2.6)

Если дифракционные искажения незначительны и условие ближней зоны выполнено, то переходят к расчету параметров электрической эквивалентной схемы ВШП. Если же нарушились неравенство (2.5) или условие ближней зоны, а материал пьезоподложки не заменялся (оператор 30), то необходимо или несколько увеличить значение ширины W апертуры ВШП, или взять с запасом значение электромагнитной развязки D_эм между ВШП, уменьшив значение А₃. Однако следует помнить, что уменьшение А₃

возможно только за счет соответствующего увеличения А₂, так как сумма А₂+A₃ должна оставаться постоянной и равной А-А₁. Затем находится новое расстояние L между ВШП и снова проверяется условие (2.5) и условие ближней зоны. В случае неоднократных нарушений условий (2.5) или (2.6) можно повторить расчет геометрических размеров фильтра для другого материала пьезоподложки (оператор 30) или вернуться к исходным данным и скорректировать техническое задание на фильтр

(oпeратор 29).

На последнем этапе расчета интегрального пьезофильтра на ПАВ определяются параметры электрической эквивалентной схемы ВШП. Широкое распространение получили простейшие эквивалентные схемы параллельного и последовательного типов, изображенные на рис.2.13,а,б. На этих схемах G_А(f)- активная проводимость излучения ВШП, R_А(f)- активное сопротивление излучения, В_А(f)- реактивная проводимость излучения, Х_А(f)- реактивное сопротивление излучения, С_Т- статическая емкость ВШП (суммарная межэлектродная емкость).

Рис.2.13. Эквивалентные электрические схемы ВШП

Реактивные составляющие BA(f) ХА(f) малы вблизи резонансной частоты f₀. Поэтому в пределах полосы пропускания обычно полагают B_A(f)=0 и Х_А(f)=0. Активная проводимость излучения

G_А(f)=G_А |H(f)|²

где G_А(f)- проводимость излучения на резонансной частоте, H(f) частотная характеристика ВШП. В случае П-образной частотной характеристики H(f) проводимость излучения можно считать постоянной и равной G_А в пределах полосы пропускания ВШП. На резонансной частоте f₀ активная проводимость излучения

G_А(f)=8k²f₀²C_T/∆f_п

где k²- коэффициент электромеханической связи материала подложки, ∆f_п- полоса пропускания фильтра. Сопротивление излучения в пределах полосы пропускания

Статическая емкость ВШП

(2.8)

где W- ширина апертуры ВШП, С- погонная межэлектродная ем­кость одной пары электродов, ω(k)- функция аподизации ВШП. Значения коэффициента k² и погонной емкости С для ряда широко используемых материалов подложки приведены в табл.2.4. Значе­ния С даны для электродов с шириной b=0,5d и шагом d=0,5λ_э.

После ввода в ЭВМ значения С (оператор 31) по формулам (2.7) и (2.8) вычисляются значения G_А и С_т (оператор 32).

Завершением расчетов является вывод на экран дисплея те­хнических характеристик фильтра (оператор 33), в которые включаются:

1. характеристика избирательности;

2. промежуточная частота f₀, МГц;

3. полоса пропускания ∆f_n , МГц;

4. фактическая неравномерность в полосе

пропускания A',дБ;

5. фактическое ослабление в полосе задерживания

В',дБ; 6) фактическая крутизна склона нормированной

АЧХ,к';

7. проводимость излучения G_A;

8. статистическая емкость С_т;

9. материал пьезоподложки; 10) функция аподизации ВШП.

Для окончательного определения топологической структуры ВШП необходимо решить вопрос о целесообразности введения ней­тральных электродов и расщеплении электродов ВШП [11].