
- •Б.Т. Добрица, и.В. Дубограй, о.В. Скуднева. Кратные интегралы и их приложения. Электронное учебное издание
- •Добрица Борис Тимофеевич Дубограй Ирина Валерьевна Скуднева Оксана Валентиновна.
- •Введение.
- •Модуль 1.
- •1.Определение двойного интеграла. Теорема о его существовании.
- •2. Свойства двойного интеграла.
- •3.Геометрический смысл двойного интеграла.
- •4. Повторный интеграл.
- •5. Переход от двойного интеграла к повторному. Расстановка пределов интегрирования.
- •1.Замена переменных в двойном интеграле.
- •2.Геометрический смысл модуля и знака Якобиана.
- •4.Обобщённые полярные координаты.
- •1.Вычисление объемов тел с помощью двойного интеграла.
- •2.Вычисление площади поверхности. Понятие площади поверхности.
- •1. Вычисление массы материальной пластинки.
- •1.Определение тройного интеграла.
- •2.Теорема существования тройного интеграла.
- •3.Свойства тройного интеграла.
- •6. Интеграл от единичной функции по области равен объёму этой области.
- •3.Сферическая система координат.
- •2. Несобственный двойной интеграл первого рода ( по неограниченной области). Интеграл Пуассона.
- •Пример аттестационного билета.
- •Приложения.
- •Типовой расчёт №1 «Кратные интегралы».
- •Задача 5.
- •Задача 6.
- •Дополнительная литература
- •Методические пособия, Кафедральные издания и методические материалы
2.Вычисление площади поверхности. Понятие площади поверхности.
Пусть G - гладкая (кусочно-гладкая) ограниченная поверхность. Разобьём её гладкими кривыми произвольно на n частей ( на n элементарных площадок) так, чтобы каждая из этих площадок однозначно проецировалась на касательную плоскость, проведённую в любой точке элементарной площадки.
На
каждой элементарной площадке
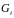 выберем произвольную точку
выберем произвольную точку
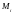 и проведём через эти точки касательные
плоскости к поверхности. Обозначим
через
и проведём через эти точки касательные
плоскости к поверхности. Обозначим
через
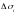 площадь проекции каждой элементарной
части на свою касательную плоскость.
Составим сумму
площадь проекции каждой элементарной
части на свою касательную плоскость.
Составим сумму
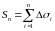 .
.
Пусть
- диаметр элементарной части
и
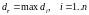 .
.
Если
существует предел
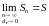 ,
то поверхность называется квадрируемой,
а число
,
то поверхность называется квадрируемой,
а число
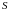 - её площадью.
- её площадью.
Наглядным примером и моделью может служить всем известный прибор – зеркальный шар для праздников. Он обклеен множеством плоских зеркальных пластинок. В пределе, при бесконечном возрастании числа пластинок, и, соответственно, уменьшении размера каждой пластинки, сумма площадей пластинок стремится к площади поверхности шара (см. рис. 3.7).

Рисунок 3.7
П усть
-
уравнение поверхности
усть
-
уравнение поверхности
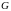 и
и
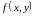 -
непрерывная дифференцируемая функция.
Напомним, что каждый участок поверхности
аппроксимируется участком касательной
плоскости
-
непрерывная дифференцируемая функция.
Напомним, что каждый участок поверхности
аппроксимируется участком касательной
плоскости
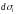 ,
нормальным вектором к которой является
градиент функции
,
нормальным вектором к которой является
градиент функции
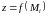 .
Представив уравнение поверхности в
виде
.
Представив уравнение поверхности в
виде
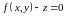 ,
вычислим градиент:
,
вычислим градиент:
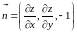 .
Координаты нормированного вектора
градиента являются направляющими
.
Координаты нормированного вектора
градиента являются направляющими
косинусами
углов
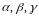 ,
которые градиент образует с осями
координат.
,
которые градиент образует с осями
координат.
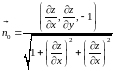
.
Рисунок 3.8
Если
спроецировать элементарную площадку
на координатную плоскость
в
элементарную площадку
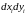 ,то
получим:
,то
получим:
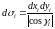 .
.
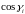 - аппликата
- аппликата
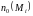 ,
а именно
,
а именно
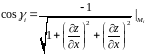 .
.
Тогда
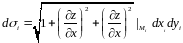 (см. рис.3.8) и площадь той части поверхности,
которая однозначно проецируется в
область
плоскости
,
как предел интегральной суммы
(см. рис.3.8) и площадь той части поверхности,
которая однозначно проецируется в
область
плоскости
,
как предел интегральной суммы
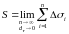 вычисляется по формуле
вычисляется по формуле
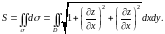 (3.3)
(3.3)
Пример
3.4 Вычислим
площадь части поверхности полусферы
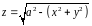 ,
вырезанной цилиндром
,
вырезанной цилиндром
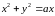 .
.
Решение.
Построим заданные поверхности и выделим
нужную часть поверхности (на рис. 3.9 она
выделена синим цветом). Поверхность
проецируется в плоскость
в область, ограниченную окружностью
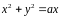 .
.
П
Рисунок 3.9
о формуле (3.3) составим интеграл для вычисления искомой площади поверхности.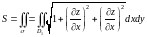
Вычислим частные производные.
Рисунок 3.10
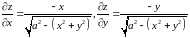
Упростим
подкоренное выражение и получим интеграл
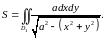 .
.
Выберем
способ его вычисления. В данном случае
удобнее перейти к полярным координатам
и учесть симметрию относительно
плоскости
.
Половина области
является радиально правильной, где
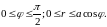 Расставим пределы интегрирования в
повторном интеграле и вычислим его.
Расставим пределы интегрирования в
повторном интеграле и вычислим его.
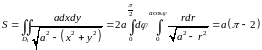 .
.
Пример 3.5 В условиях предыдущего примера вычислить площадь боковой поверхности части цилиндра, заключённой между полусферой и плоскостью .
Р
Рисунок 3.11
ешение. На рис. 3.10 зелёным цветом выделена половина заданной части цилиндра . Очевидно, что эта часть удобно, без наложения, проецируется только на координатную плоскость . Граница области , в которую проецируется при этом зелёная часть цилиндра, состоит из трёх частей. Две из них очевидны, это и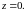 Третья часть является проекцией линии
пересечения полусферы и цилиндра. Чтобы
спроецировать линию пересечения на
плоскость
,
необходимо построить проецирующий
цилиндр, направляющей которого является
эта линия, с образующей, параллельной
оси
Третья часть является проекцией линии
пересечения полусферы и цилиндра. Чтобы
спроецировать линию пересечения на
плоскость
,
необходимо построить проецирующий
цилиндр, направляющей которого является
эта линия, с образующей, параллельной
оси
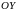 .
Уравнение этого цилиндра совпадёт с
уравнением проекции линии пересечения
двух поверхностей на плоскость
.
(См. замечание 1)
.
Уравнение этого цилиндра совпадёт с
уравнением проекции линии пересечения
двух поверхностей на плоскость
.
(См. замечание 1)
И з
системы уравнений, задающих полусферу
и цилиндр, исключим переменную y.
з
системы уравнений, задающих полусферу
и цилиндр, исключим переменную y.
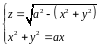
Получим
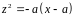 .
Это уравнение цилиндра параболического.
Третьим участком границы области
является часть параболы.
.
Это уравнение цилиндра параболического.
Третьим участком границы области
является часть параболы.
П
Рисунок 3.10
остроим область (см. рис.3.11).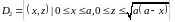 .
.
Интеграл для вычисления площади поверхности в данном случае имеет вид:

Рисунок 3.11
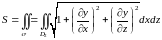 ,
,
где
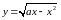 - уравнение, задающее цилиндр. Эта формула
получена из формулы (3.3), в которой роль
функции играет
- уравнение, задающее цилиндр. Эта формула
получена из формулы (3.3), в которой роль
функции играет
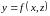 ,
а переменными интегрирования являются
и
.
,
а переменными интегрирования являются
и
.
Вычислим частные производные.
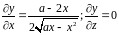 .
.
Упростим подкоренное выражение, подставим его в выбранную формулу и вычислим интеграл.
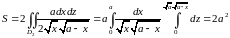
Домашнее задание к занятию 3:
ОЛ-6 №№ 2197, 2199, 2204, 2210, 2213, 2217, 2218 или ОЛ-5 №№ 8.82, 84, 85, 71, 72, 73.
Занятие 4.
Вычисление с помощью двойного интеграла массы материальной пластинки, ее статических моментов, центров масс и моментов инерции.
Ауд.: ОЛ-6 №№ 2225, 2227, 2228, 2231, 2237 или ОЛ-5 №№ 8.92, 94, 97, 98, 99.
