4.Обобщённые полярные координаты.
При решении некоторых задач удобна следующая замена переменных, которая существенно упрощает вычисление интеграла.
,
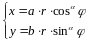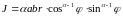
Здесь
переменные
называются обобщёнными полярными
координатами.
Пример
2.2 Вычислим
площадь области, ограниченной астроидой
.
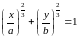Решение. Построим астроиду (см. рис. 2.5).
Введём
обобщённые полярные координаты:
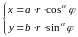, и
показатель α подберём так, чтобы при
подстановке в уравнение астроиды
получилось уравнение единичной
окружности. Для данной задачи такой
показатель равен трём.
Рисунок 2.5
Действительно,
,
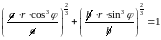или
.
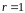Якобиан
отображения при этом равен
.
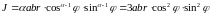Далее, по формуле (2.4) составим интеграл для вычисления искомой площади :
Область
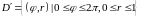является
радиально правильной. Расставим пределы
в повторном интеграле и вычислим его.
.
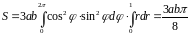Замечание.
После расстановки пределов интегрирования
оказалось возможным взять интегралы
по
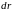и
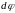отдельно друг от друга, как их произведение,
поскольку пределы внутреннего
интегрирования постоянны.
Домашнее задание к занятию 2:ОЛ-6 №№2161, 2163, 2167, 2170, 2181 или ОЛ-5 №№ 8.42, 45, 49, 51, 60, 63.
Дополнительный
пример 2.3.
Вычислить площадь замкнутой области
,
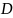образованной пересечением следующих
кривых:
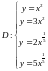
Решить задачу с помощью перехода к новой системе координат. Проверить решение в среде MathCad.
Решение.
Если
ввести координаты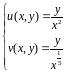
, то в системе координат
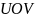область
отобразится
в область
,
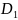представляющую собой прямоугольник,
заключённый в пределах
,
.
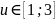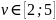(См. рис.2.6)
Рисунок 2.6
Для вычисления площади области D применим формулу :
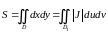
Сначала
выразим переменные x
и
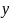через
u
и v,
так как для вычисления Якобиана
преобразования нам необходимо осуществить
переход
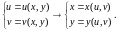Получим
систему:
.
Якобиан
преобразования :
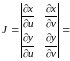
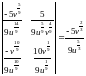
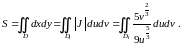
Область , напомним, представляет собой прямоугольник (см.рис.2.6), подынтегральная функция может быть разбита на множители, поэтому при переходе от двойного интеграла к повторному он распадётся на произведение двух независимо вычисляемых интегралов:
.
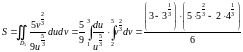Проверка решения в среде MathCad.
Для
начала работы нам понадобится представление
,
в нашей задаче это
.
Запись произведём с помощью значка «:=» на панели «Вычисления» или «Калькулятор».
Рисунок 2.8
Затем откроем панель инструментов “f(x)” («Вставить функцию»). В левом столбце выбираем категорию функции – «Решение дифференциального уравнения», в правом столбце находим функцию Jacob и нажимаем кнопку «ОК».
Рисунок 2.9
Аргументы функции Jacob - две матрицы, записанные через запятую.
Первая
матрица-столбец – это определённые
ранее функци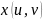и
и
,
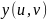вторая – матрица-столбец, состоящая из
переменных, по которым будет произведено
дифференцирование, в нашей задаче это
.
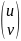Задать матрицу требуемого размера можно
с помощью кнопки на панели «Матрица».
Рисунок 2.10
Если
далее на панели «Вычисления» выбрать
значок
, программа
выведет на экран матрицу Якоби. Чтобы
вычислить её определитель, Якобиан, на
панели «Матрица» нажмём на кнопку
, вместо х вставим предыдущую запись .
Рисунок 2.13
Осталось записать двойной интеграл и сверить полученное нами и вычисленное компьютером значение площади области . Как видим, ошибки нет.
Рисунок 4.12
Занятие 3.
Вычисление объемов тел с помощью двойного интеграла. Вычисление площади поверхности в декартовых координатах с помощью двойного интеграла.
Ауд.: ОЛ-6 №№2198, 2200, 2203, 2219, 2214, 2216 или ОЛ-5 №№8.69, 70, 76, 85, 86, 88