1.Замена переменных в двойном интеграле.

Вычисление двойного интеграла может оказаться затруднительным, и тогда ищут другую систему координат, в которой интегрирование упростилось бы. При этом происходит преобразование переменных, а также и области интегрирования.

Рисунок 2.1

Пусть взаимно однозначное отображение области D' плоскости UOV

в область D плоскости XOY задано функциями 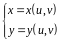, (2.1)

причём обе функции непрерывно дифференцируемы в области D' .

(см. рис 2.1) При этом отображении площадь элементарной части 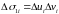области 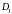и площадь 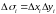соответствующей части области связаны так, что 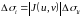, где 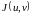- якобиан этого отображения, отличный от нуля в любой точке области D' , кроме, быть может, конечного числа точек (линий), т.е.

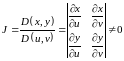(2.2)

Тогда справедлива формула замены переменных для двойного интеграла:

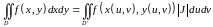(2.3)

Замечание.При переходе в новую систему координат площадь плоской фигуры (См. свойства двойного интеграла) вычисляется по формуле: 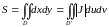(2.4)

2.Геометрический смысл модуля и знака Якобиана.

Модуль якобиана есть предел отношения площадей бесконечно малых площадок ΔD  и ΔD΄.

Геометрический смысл знака якобиана состоит в том, что в случае положительного якобиана ориентации контуров, ограничивающих области D' и D при отображении совпадают, а при отрицательном — отличаются.

3.Двойной интеграл в полярной системе координат (как частный случай).

Связь между переменными в декартовой и полярной системах координат:

(см. рис. 2.2)

Рисунок 2.2

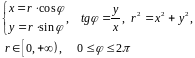(2.5)

Я

Рисунок 2.3

кобиан при переходе в полярную систему координат: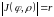 . (Убедитесь в этом, вычислив якобиан самостоятельно по формуле (2.2))

Теперь формула (2.3) примет вид:

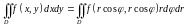(2.6)

Заметим, что при переходе к полярным координатам область не меняется.

Область интегрирования в полярной системе координат назовём радиально правильной, если она заключена в секторе между лучам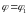и и 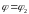и ограничена в нём двумя, не пересекающимися во внутренних точках сектора, кривыми с уравнениями 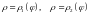. (См. рис. 2.3)

Т

огда двойной интеграл по такой области преобразуется в повторный следующим образом:

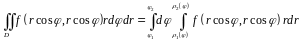(2.7)

Площадь плоской фигуры в полярной системе координат вычисляется по формуле

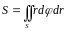(2.8)

Замечание. К полярным координатам удобно переходить, когда подынтегральная функция зависит от 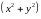и в уравнениях границы области содержится эта же комбинация.

Пример 2.1 Область задана неравенствам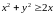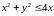и , и 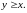Преобразуем двойной интеграл 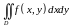в повторный, изменим порядок интегрирования и перейдём к полярным координатам.

Решение. Построим заданную область, ограниченную двумя окружностями и прямой (см. рис. 2.4).

Выразим поочерёдно из уравнений всех частей границы, чему равны переменные 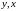. Перейдём к полярной системе и выразим

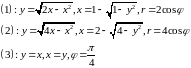
(Обратите внимание на знаки перед корнями!)

Данная область не является - правильной, т.к. её нижняя граница состоит из двух частей. Поэтому разобьём её на две части прямой так, чтобы в каждой из этих частей было по одной нижней границе (см. рис. 2.4).

Рисунок 2.4

Тогда .

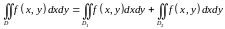В - правильной области переменные изменяются так, что .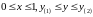

В - правильной области 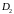имеем .

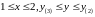И тогда

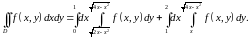
Пределы интегрирования в повторном интеграле расставлены.

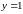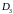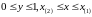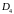
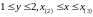Поменяем порядок интегрирования. Область не является - правильной, т.к. её правая граница состоит из двух частей. Поэтому разобьём её на две части прямой так, чтобы в каждой из этих частей было по одной правой границе (см. рис. 2.4). Тогда в - правильной области переменные изменяются так, что , а в - правильной области . И теперь

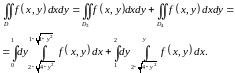
Далее расставим пределы в повторном интеграле, перейдя к полярным координатам. Область в полярной системе координат является радиально правильной, т.к. в ней переменные изменяются так, что 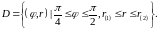Отсюда следует, что

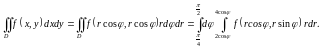
Выполнены все три варианта расстановки пределов в повторных интегралах.