
- •Індивідуальні завдання Елементи лінійної алгебри
- •Елементи аналітичної геометрії
- •Комплексні числа
- •Вступ до математичного аналізу
- •Похідна і диференціал. Правила і методи диференціювання
- •Деякі застосування похідної
- •Невизначений інтеграл
- •Визначений інтеграл. Застосування визначеного інтеграла
- •Диференціальне числення функції декількох змінних
- •Диференціальні рівняння
- •Рекомендована література
МІНІСТЕРСТВО ОСВІТИ І НАУКИ,
МОЛОДІ ТА СПОРТУ УКРАЇНИ
КІРОВОГРАДСЬКИЙ НАЦІОНАЛЬНИЙ
ТЕХНІЧНИЙ УНІВЕРСИТЕТ
ФАКУЛЬТЕТ ПРОЕКТУВАННЯ І ЕКСПЛУАТАЦІЇ МАШИН КАФЕДРА ВИЩОЇ МАТЕМАТИКИ ТА ФІЗИКИ
ВИЩА МАТЕМАТИКА
Частина ІІ
Індивідуальні завдання для студентів економічних спеціальностей
КІРОВОГРАД
2012
Вища математика. Ч. ІІ: Індивідуальні завдання для студентів економічних спеціальностей / Укл.: Гуцул В.І., Якименко С.М., Гончарова С.Я., Філімоніхіна І.І. – Кіровоград: КНТУ, 2012. – 87 с.
Друга частина містить індивідуальні завдання по всім розділам курсу вищої математики, яки вивчаються на економічних спеціальностях. Вказані завдання призначені для закріплення теоретичного матеріалу та для організації самостійної і індивідуальної роботи студентів.
Орієнтовано на студентів економічних спеціальностей.
Затверджено на засіданні
кафедри вищої
математики та фізики.
Протокол № 6 від 29.02.2012
© В.І.Гуцул,
С.М.Якименко,
С.Я.Гончарова,
І.І.Філімоніхіна, 2012
© КНТУ
ЗМІСТ
Індивідуальні завдання 4
Елементи лінійної алгебри 4
Елементи аналітичної геометрії 12
Комплексні числа 18
Вступ до математичного аналізу 21
Похідна і диференціал. Правила і методи диференціювання 29
Деякі застосування похідної 40
Невизначений інтеграл 44
Визначений інтеграл. Застосування визначеного інтеграла 56
Диференціальне числення функції декількох змінних 65
Диференціальні рівняння 75
Рекомендована література 87
Індивідуальні завдання Елементи лінійної алгебри
Завдання
1.
Знайти матрицю
![]() ,
де
,
де
![]() - одинична матриця третього порядку.
- одинична матриця третього порядку.
1.
 ;
;
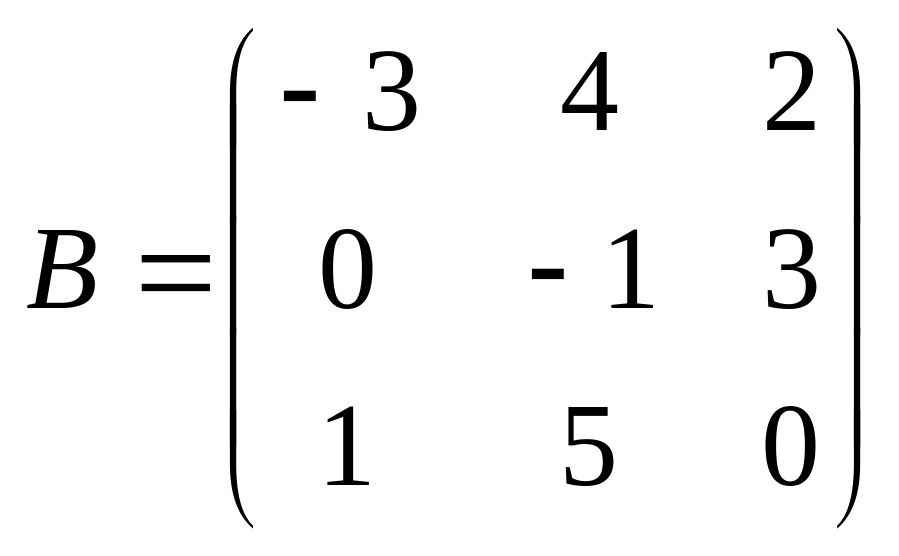 .
.
2.
 ;
;
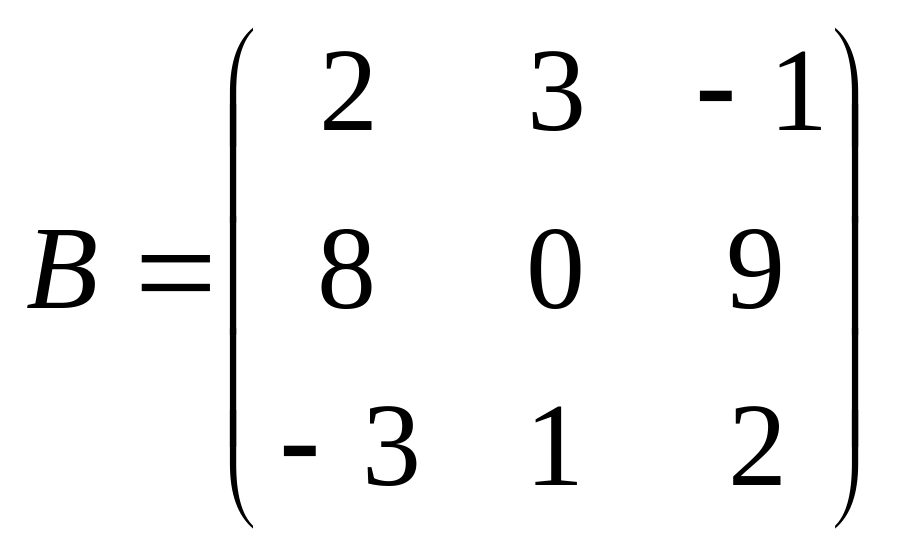 .
.
3.
 ;
;
 .
.
4.
 ;
;
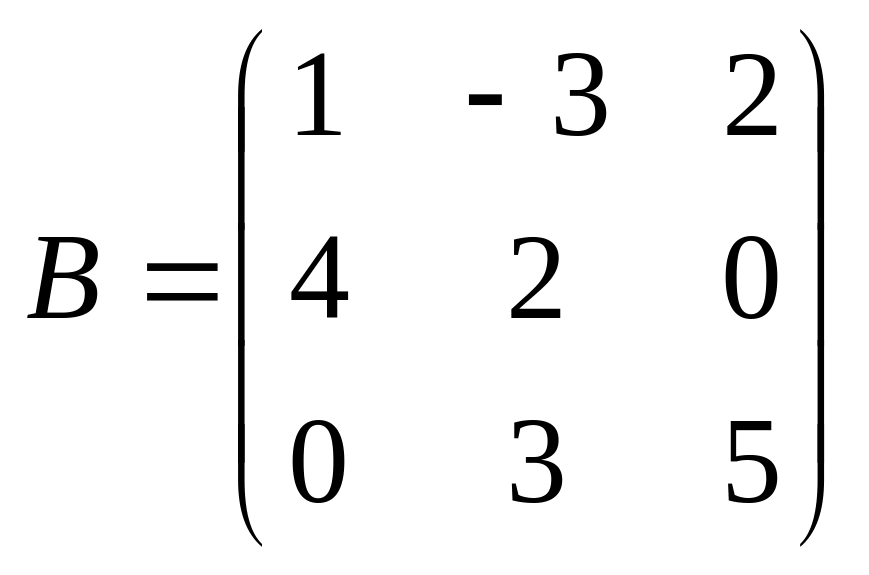 .
.
5.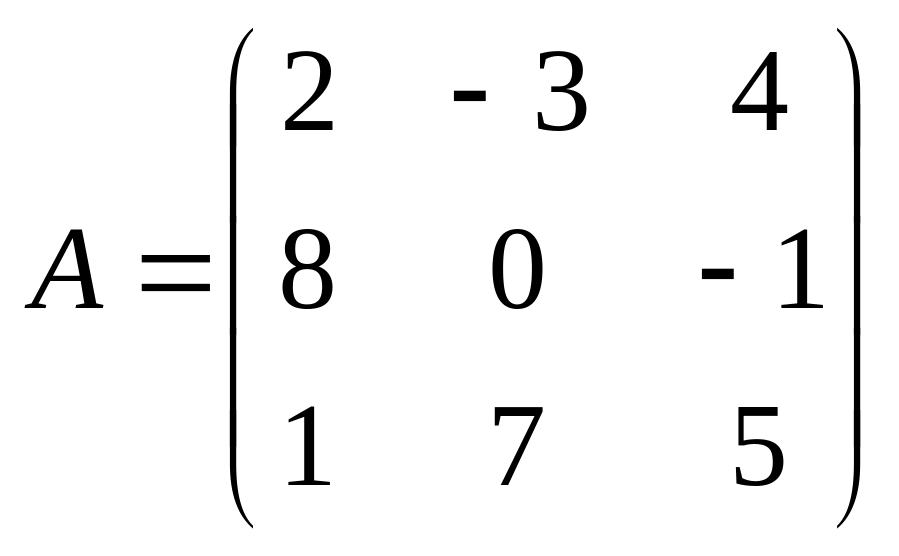 ;
;
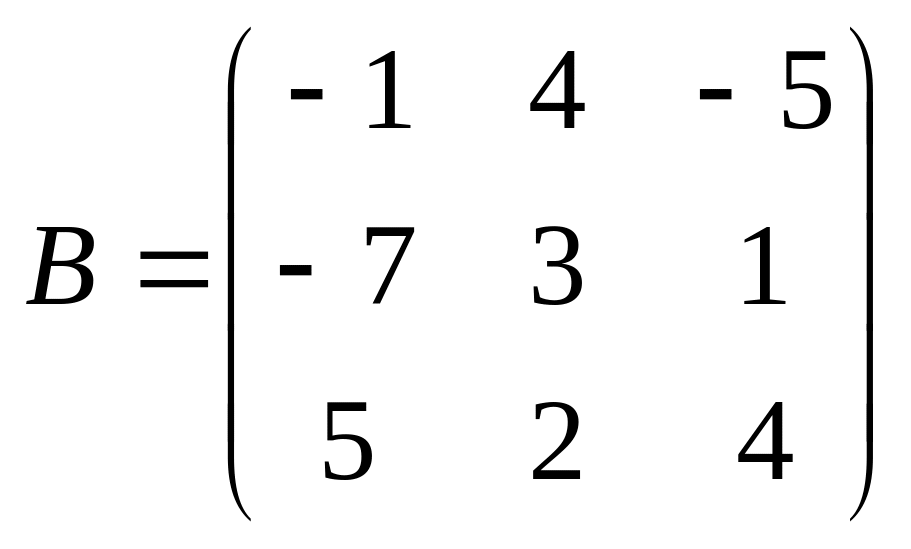 .
.
6.
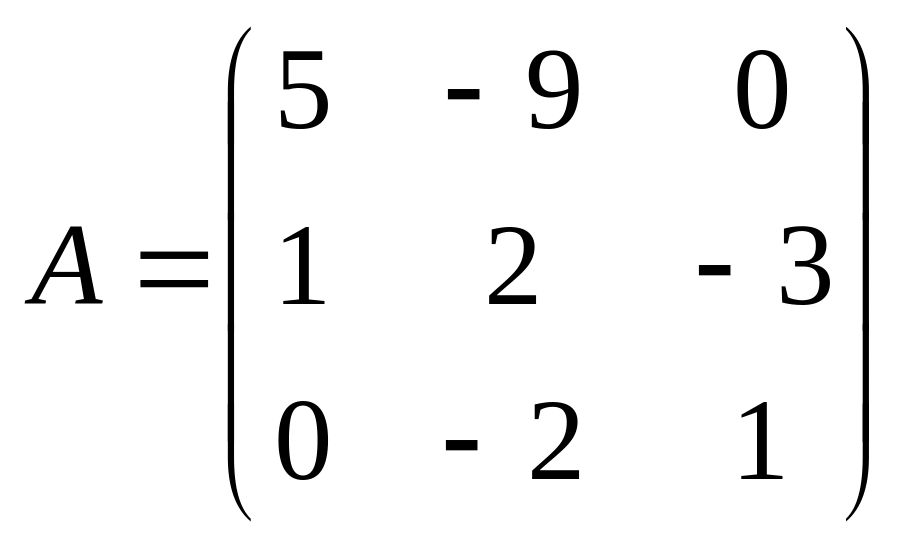 ;
;
 .
.
7.
 ;
;
 .
.
8.
 ;
;
 .
.
9.
 ;
;
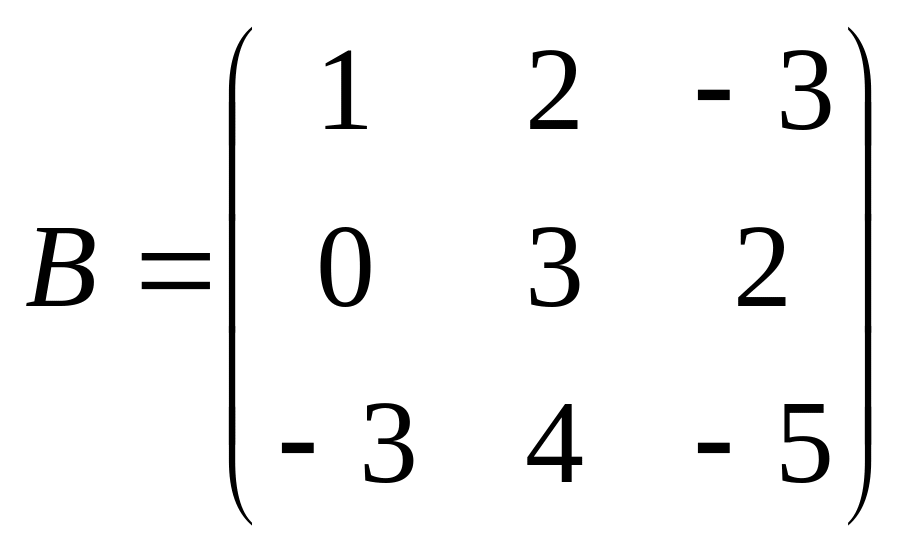 .
.
10.
 ;
;
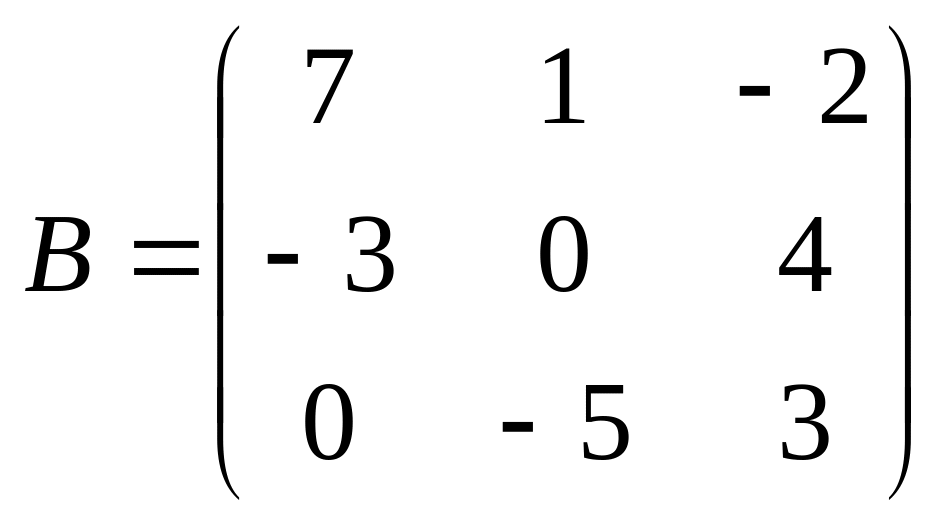 .
.
11.
 ;
;
 .
.
12. ;
;
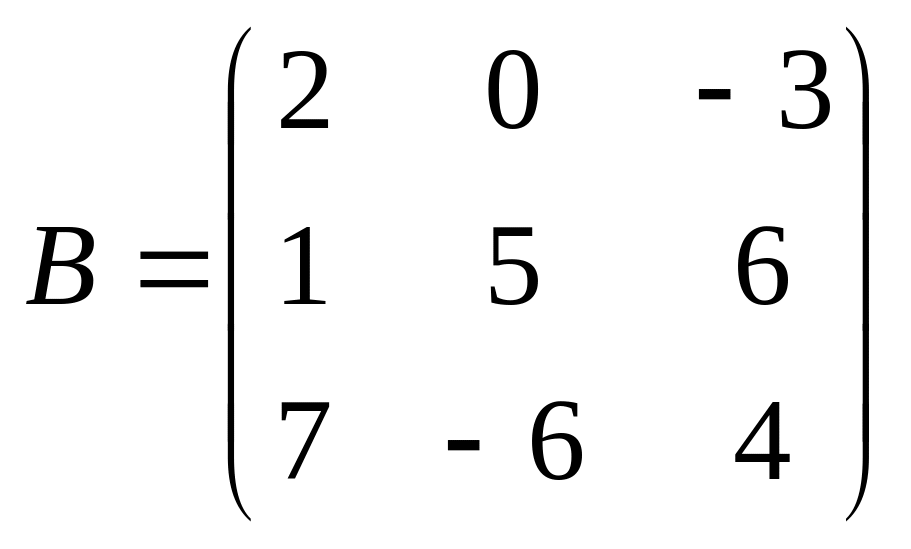 .
.
13.
 ;
;
 .
.
14.
 ;
;
 .
.
15.
 ;
;
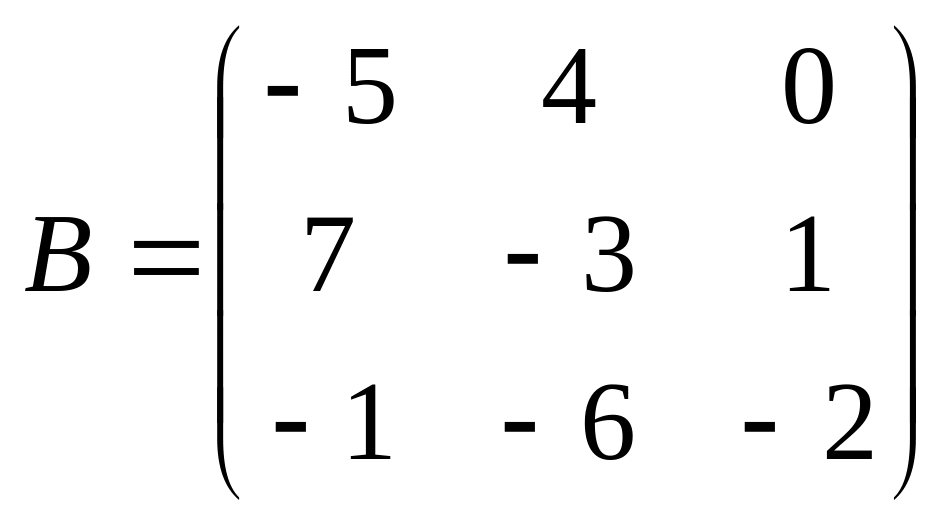 .
.
16.
 ;
;
 .
.
17.
 ;
;
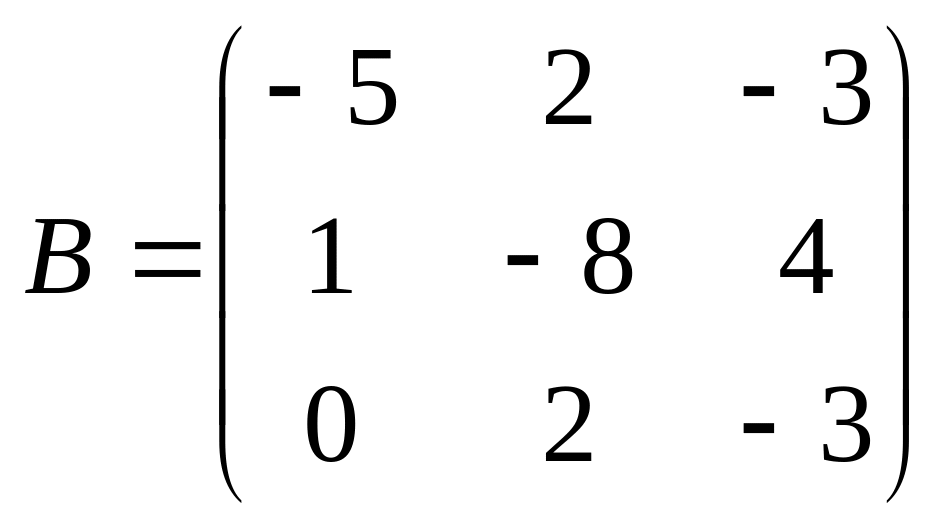 .
.
18.
 ;
;
 .
.
19.
 ;
;
 .
.
20.
 ;
;
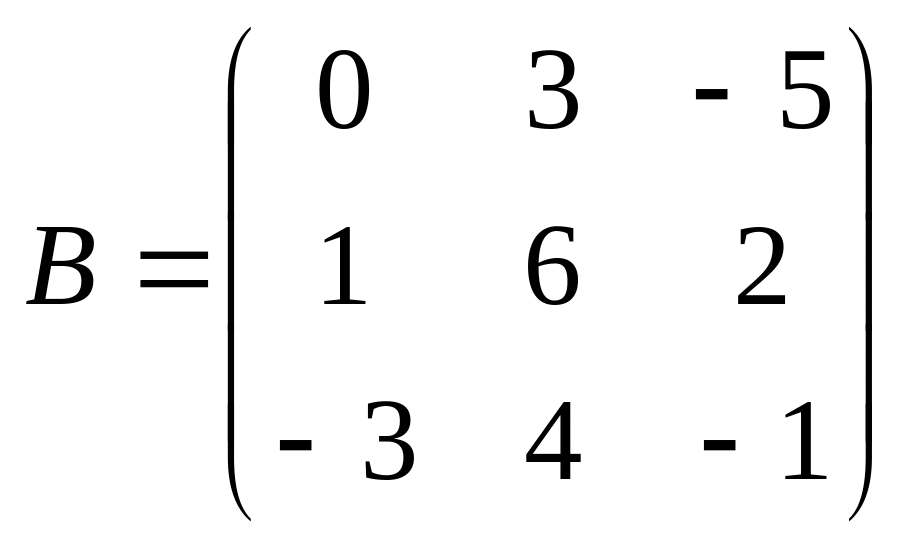 .
.
21.
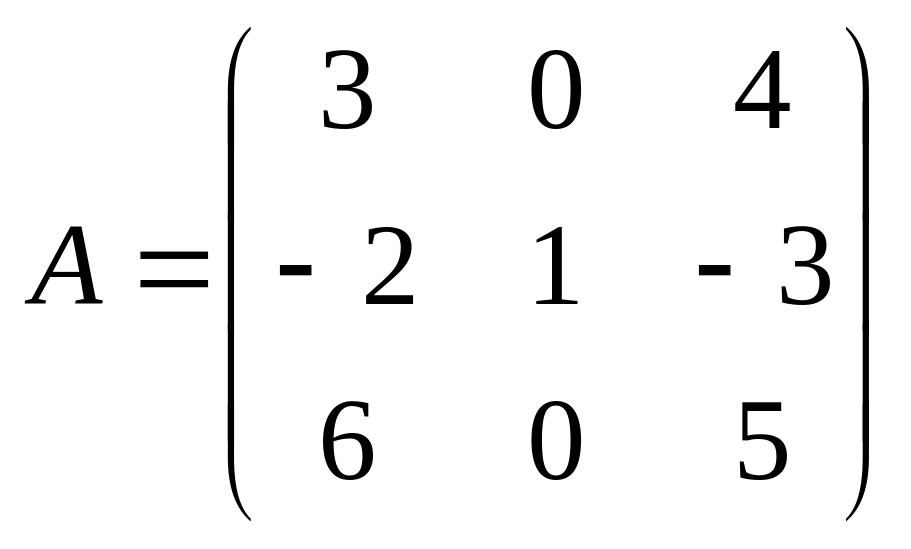 ;
;
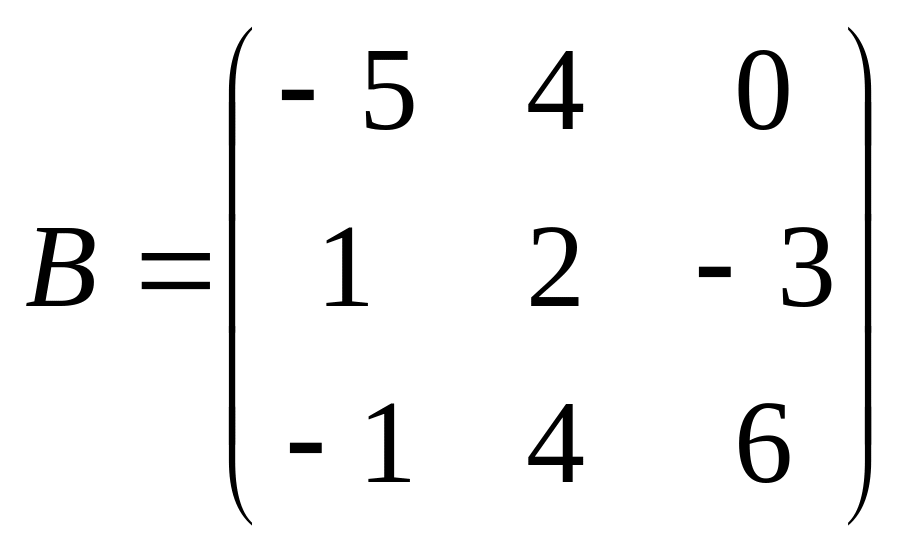 .
.
22.
;
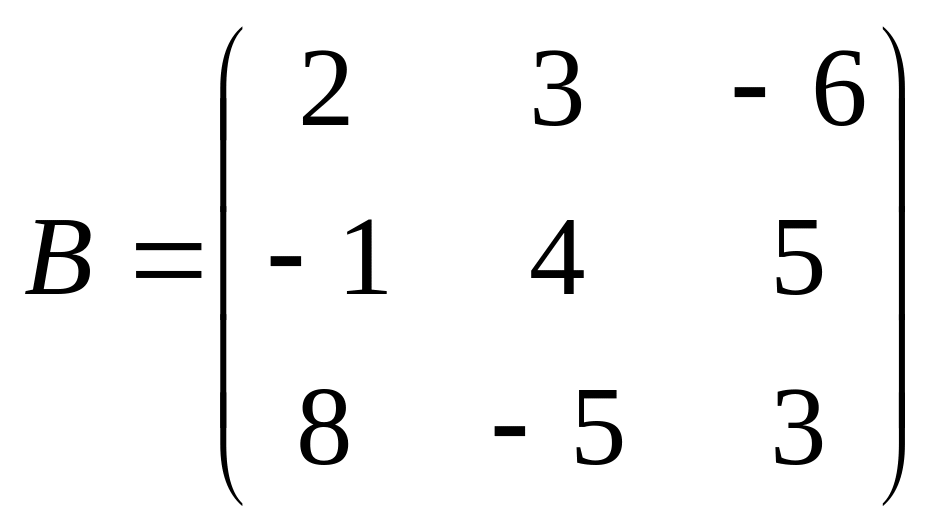 .
.
23.
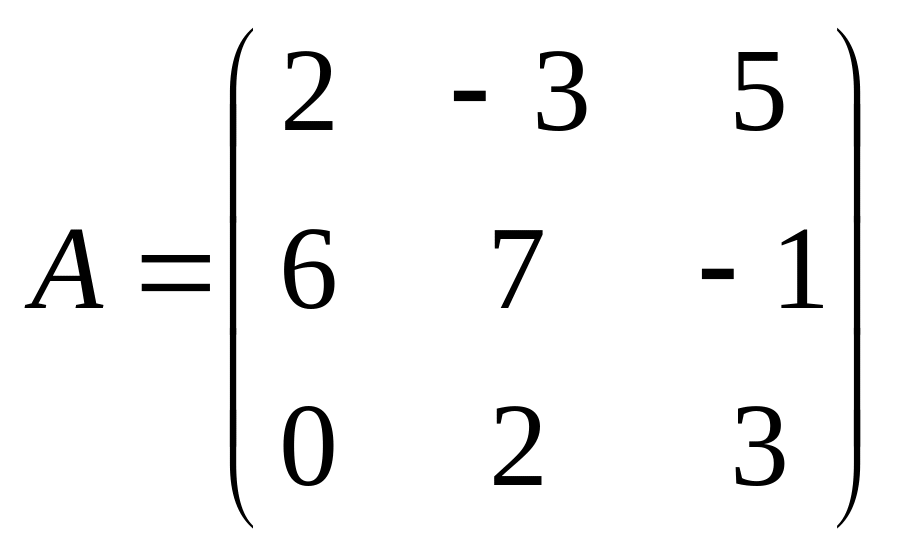 ;
;
 .
.
24.
 ;
;
 .
.
25.
 ;
;
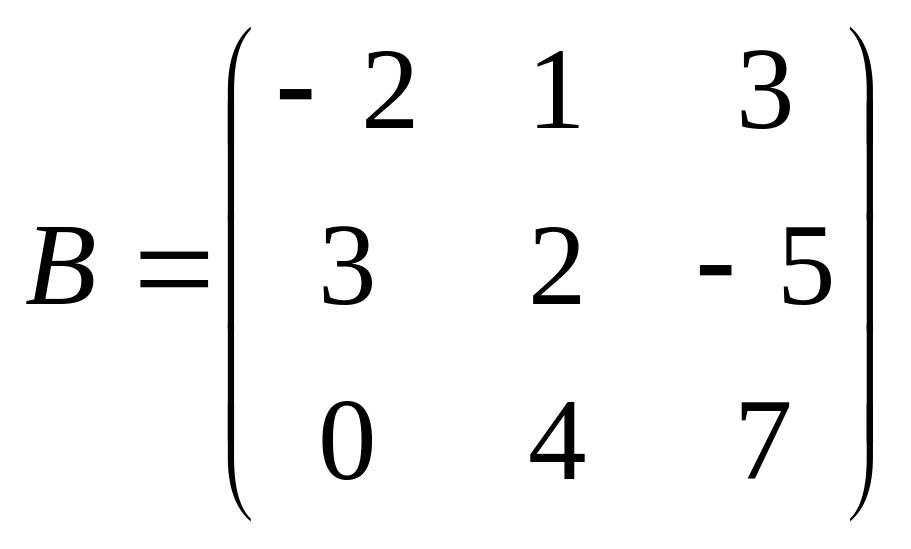 .
.
26.
 ;
;
 .
.
27.
;
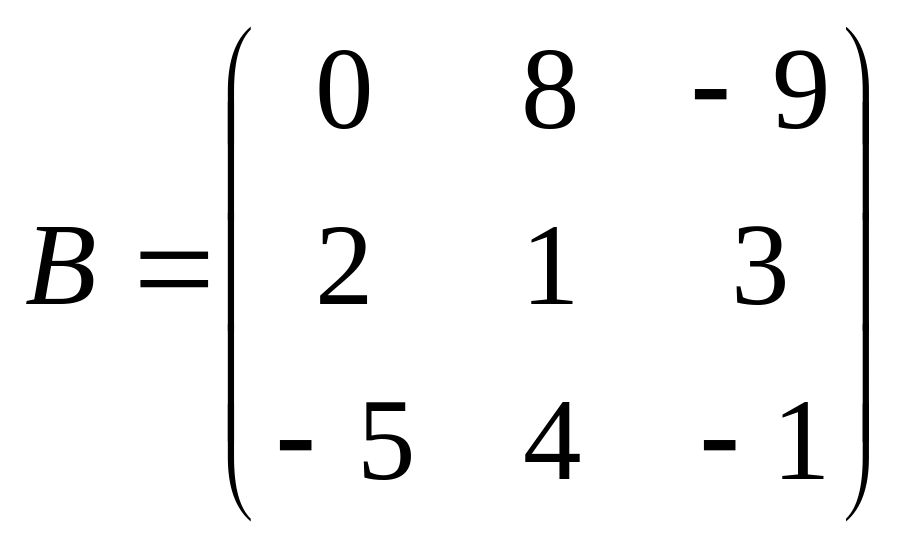 .
.
28.
 ;
;
 .
.
29. ; .
30.
 ;
;
 .
.
Завдання 2. Обчислити визначник, використовуючи:
а) метод трикутників;
б) розклад визначника за елементами рядка або стовпця;
в) властивості визначника (зведення визначника до трикутного вигляду).
1.
 .
2.
.
2.
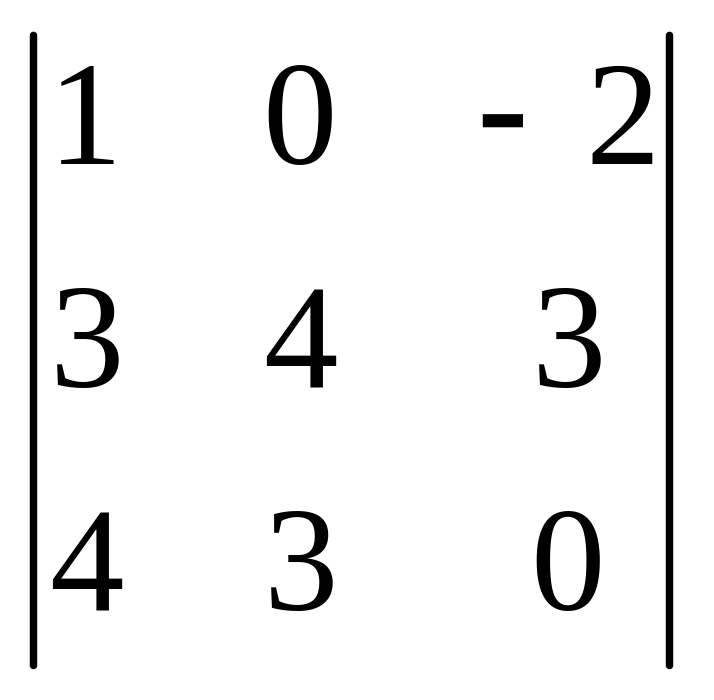 .
3.
.
3.
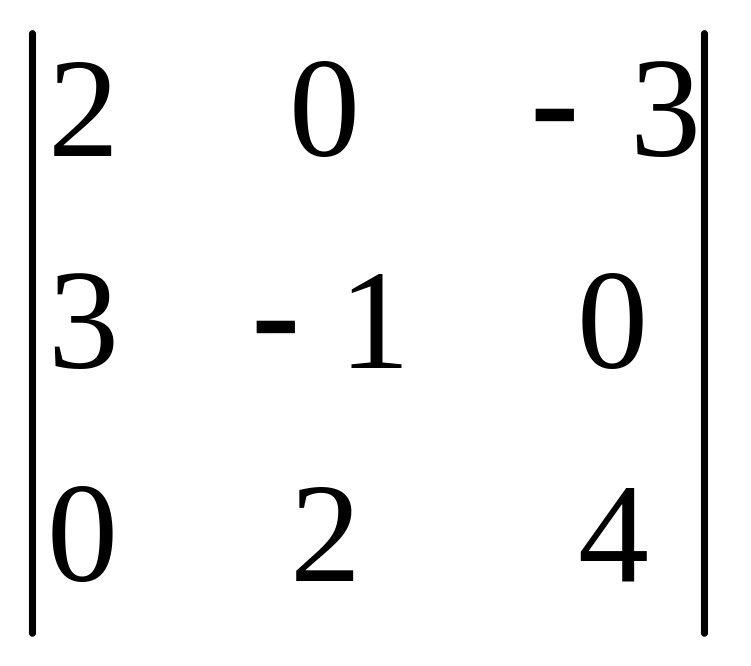 .
.
4.
 .
5.
.
5.
 .
6.
.
6.
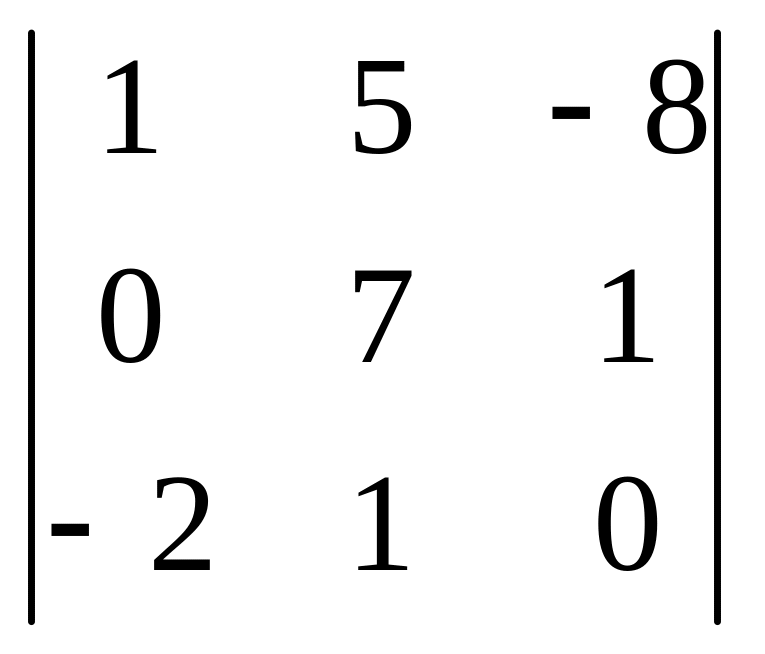 .
.
7.
 .
8.
.
8.
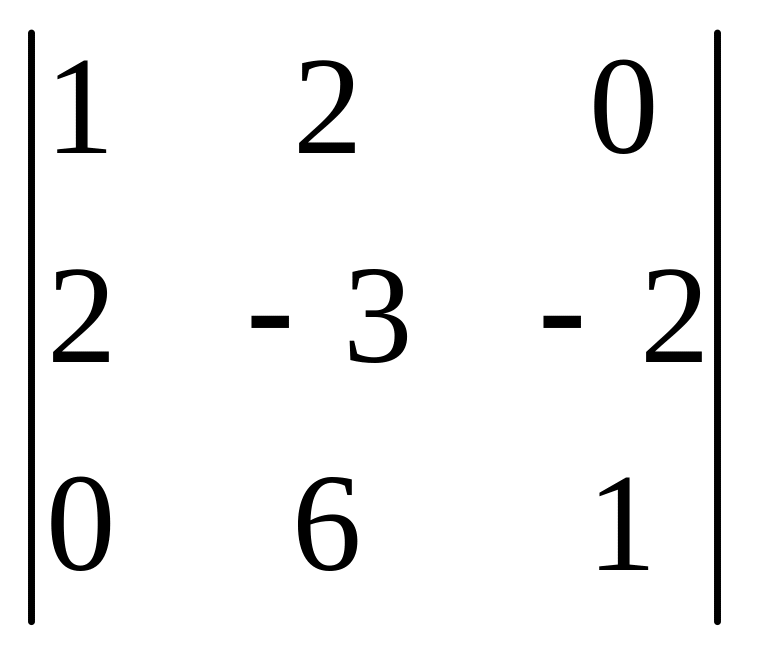 .
9.
.
9.
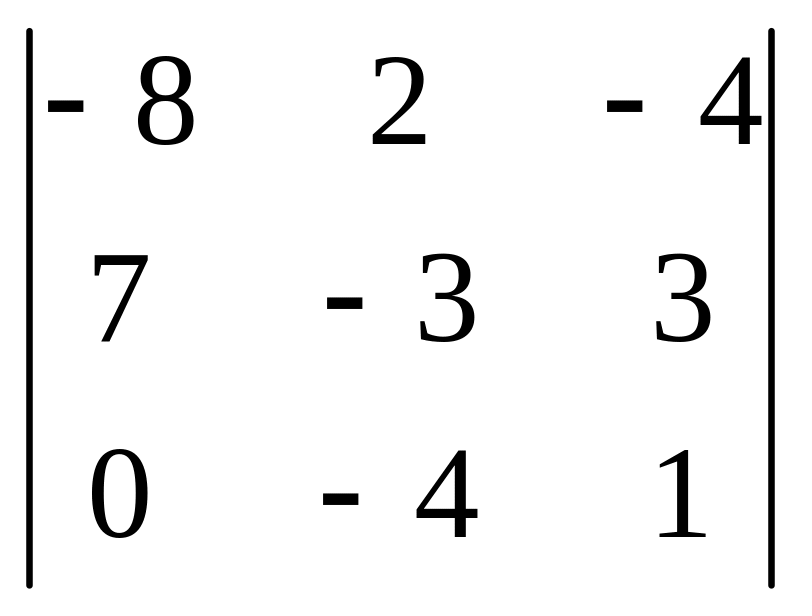 .
.
10.
 . 11.
. 11.
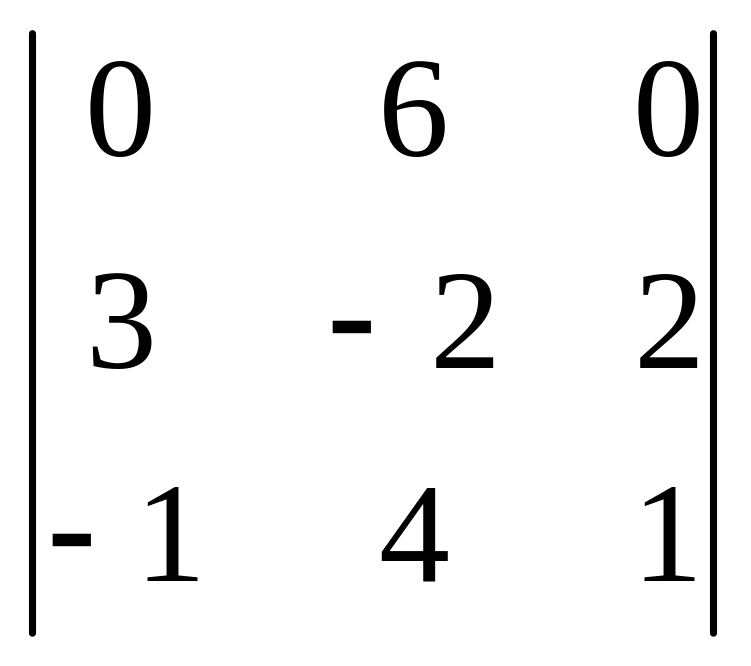 .
12.
.
12.
 .
.
13.
. 14.
 .
15.
.
15.
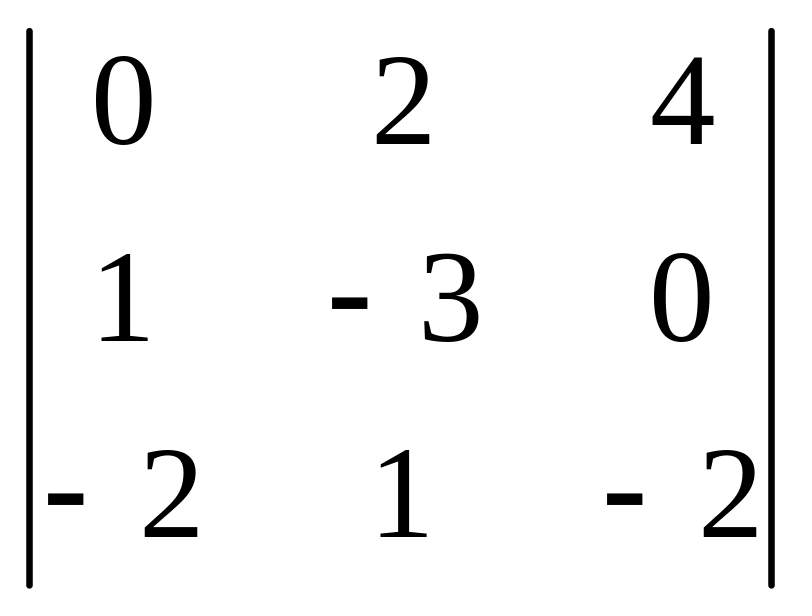 .
.
16.
 . 17.
. 17.
 . 18.
. 18.
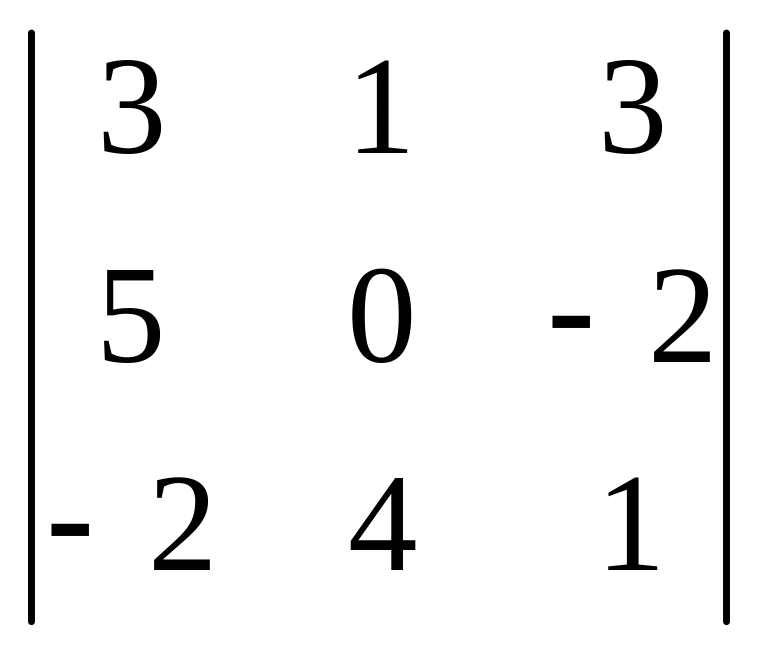 .
.
19.
 . 20.
. 20.
 . 21.
. 21.
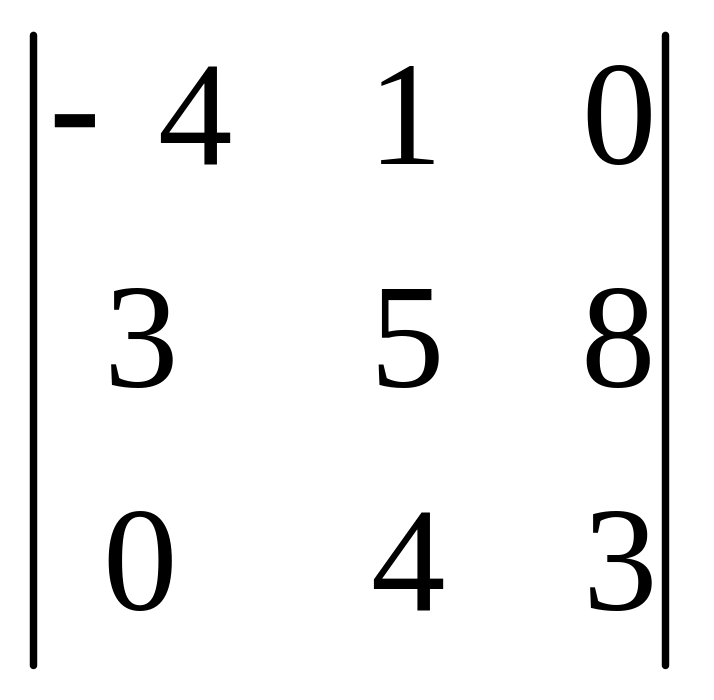 .
.
22.
 . 23.
. 23.
 24.
24.
 .
.
25.
 . 26.
. 26.
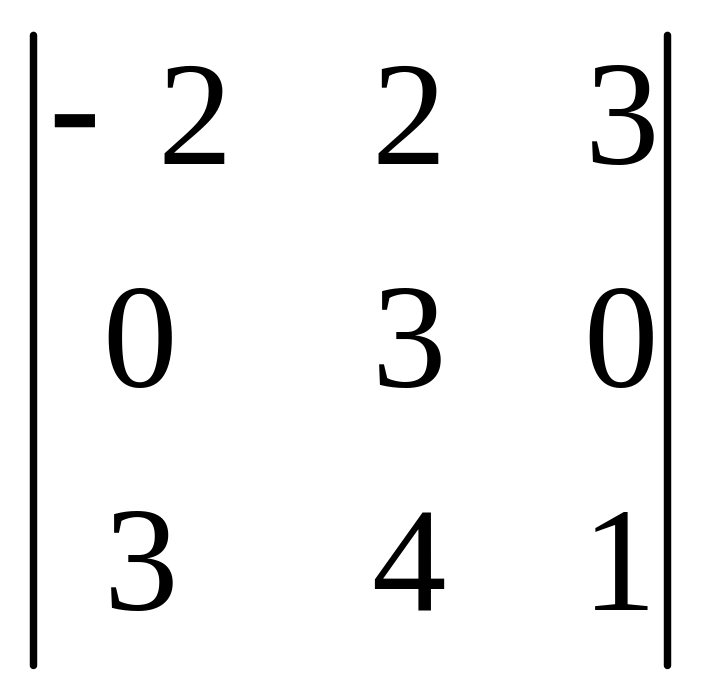 . 27.
. 27.
 .
.
28.
 . 29.
. 29.
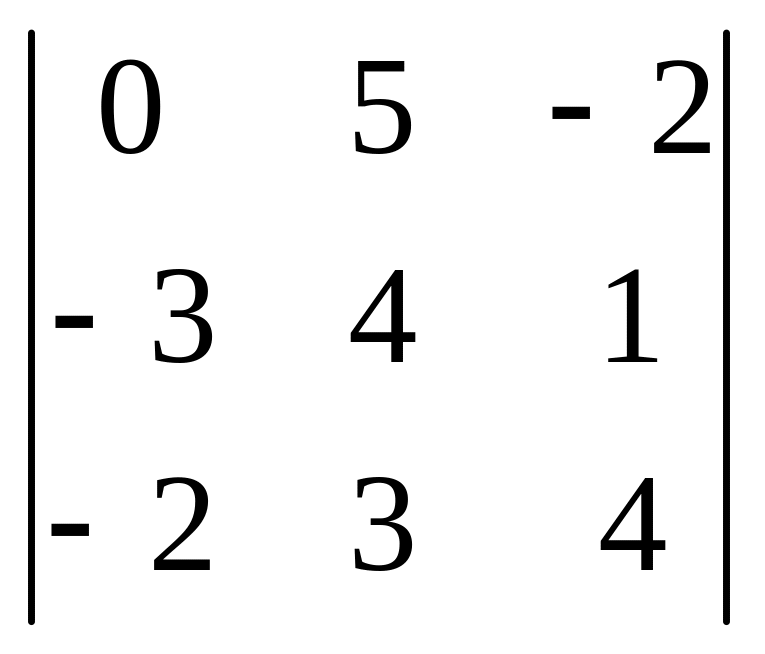 . 30.
. 30.
 .
.
Завдання 3. Перевірити на сумісність систему рівнянь і, у випадку сумісності, розв’язати її: а) за формулами Крамера; б) за допомогою оберненої матриці (матричним методом); в) методом Гаусса; г) методом Жордана-Гаусса.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]()
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
Завдання 4. Знайти загальний розв’язок однорідної системи лінійних алгебраїчних рівнянь.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.![]()
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
25.![]() 26.
26.![]()
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
Елементи аналітичної геометрії
Завдання
5.
Довести, що вектори![]() ,
,
![]() ,
,
![]() утворюють
базис, і знайти координати вектора
утворюють
базис, і знайти координати вектора
![]() у цьому базисі.
у цьому базисі.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Завдання
6.
Вершини піраміди знаходяться в точках
![]()
![]() і
і
![]() Обчислити: а) координати векторів
Обчислити: а) координати векторів
![]() ;
б) вектор
;
б) вектор
![]() ;
в) скалярний добуток
;
в) скалярний добуток
![]() та кут
та кут
![]() ;
г) векторний добуток
;
г) векторний добуток
![]() та площу трикутника АВС;
д) мішаний добуток
та площу трикутника АВС;
д) мішаний добуток
![]() та об’єм піраміди
та об’єм піраміди
![]()
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Завдання
7. Задано
вершини трикутника
![]()
![]() Знайти:
Знайти:
а)
рівняння сторони
![]() ;
;
б)
рівняння висоти
![]() ;
;
в)
рівняння та довжину медіани
![]() ;
;
г)
точку
![]() перетину медіани
та висоти
;
перетину медіани
та висоти
;
д) рівняння прямої, яка проходить через точку паралельно до сторони ;
е)
відстань від точки
![]() до прямої
(довжину висоти
).
до прямої
(довжину висоти
).
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]()
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
Завдання
8. Задано
чотири точки
![]()
![]() Знайти:
Знайти:
а)
рівняння площини
![]()
б)
рівняння площини, яка проходить через
точку
![]() перпендикулярно
до прямої
перпендикулярно
до прямої
![]()
в) рівняння прямої
г)
рівняння прямої
![]() перпендикулярної до площини
перпендикулярної до площини
д)
рівняння прямої
![]() паралельної
до прямої
паралельної
до прямої
е)
синус кута між прямою
![]() та площиною
та площиною
є)
косинус кута між координатною площиною
![]() і площиною
і площиною
![]()
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
