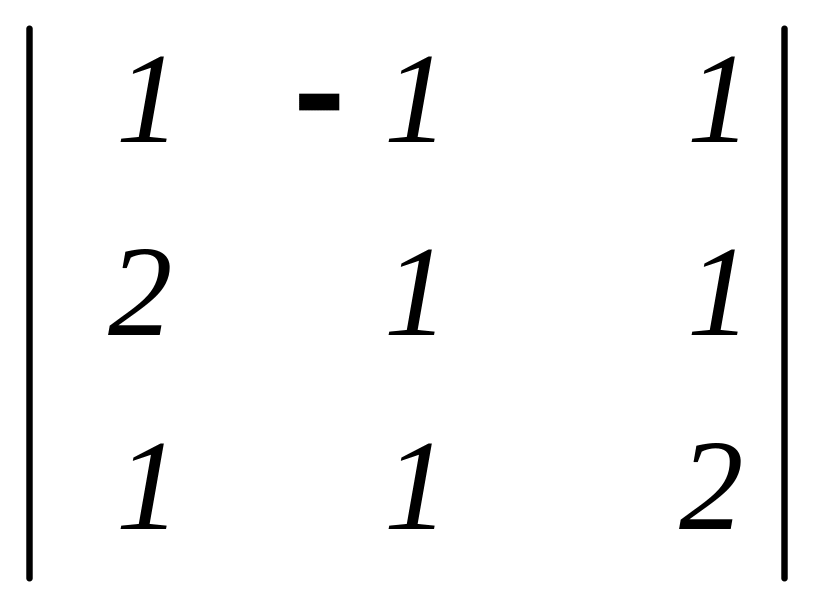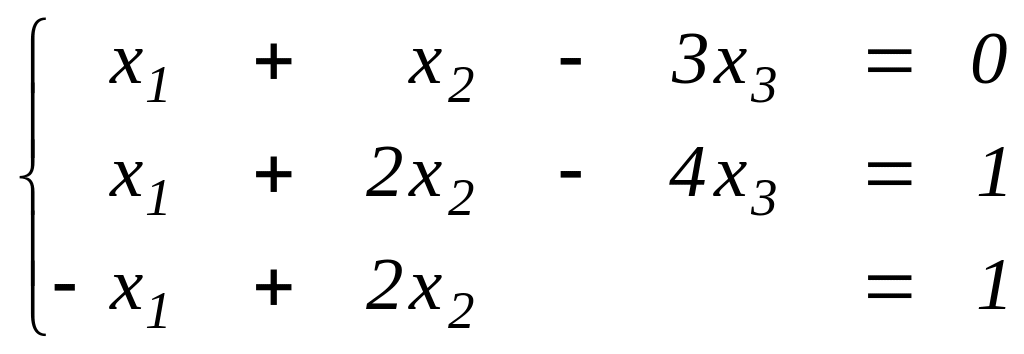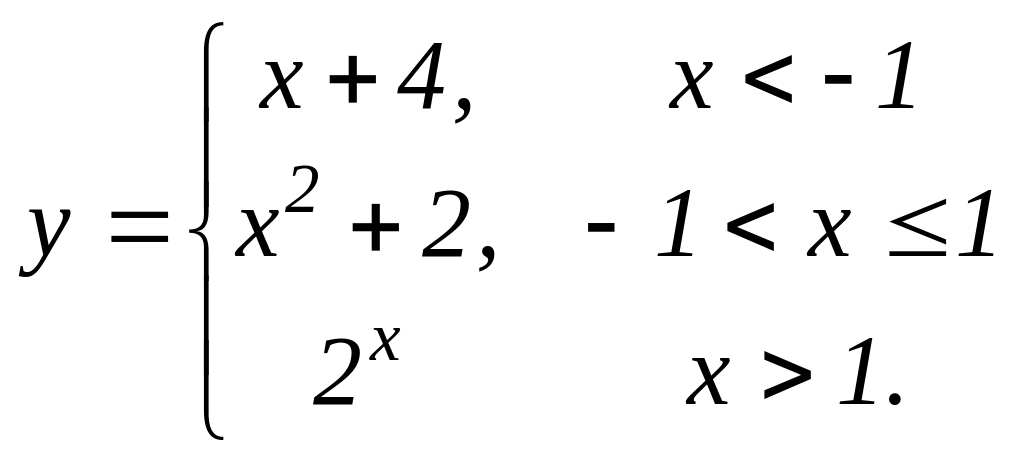Контрольная работа №1.

№

Задание 1.

Задание 2.

Задание 3.

,

а) б)

,

а) б)

,

а) б)

,

а) б)

,

а) б)

,

а) б)

,

а) б)

,

а) б)

,

а) б)

,

а) б)

Понятие матрицы, виды матриц.

Действия над матрицами.

Понятие определителя, минора элемента матрицы ого порядка, алгебраического дополнения элемента матрицы ого порядка.

Основные свойства определителей

Методы вычисления определителей.

Вычисление обратной матрицы.

Системы линейных уравнений: матричная запись, структура множества решений однородной и неоднородной системы. Формы записи.

Матричный метод решения системы линейных алгебраических уравнений.

Формулы Кремера для решения систем линейных уравнений с квадратной матрицей.

Решение систем линейных уравнений методом Гаусса.

Задание 1.

Задание 2.

Понятие функции (отображения). График функции. Чётность, нечётность и периодичность функции. Сложная функция.

Предел функции в точке. Основные теоремы о пределах Признаки существования предела

Предел функции на бесконечности ( ). Односторонние пределы. Замечательные пределы.

Бесконечно малые и бесконечно большие функции ( Б.М.Ф и Б.Б.Ф.). Связь бесконечно большими и бесконечно малыми функциями. Сравнение бесконечно малых.

Непрерывность функции в точке ( на языке “ε - δ“ и на языке последовательностей). Непрерывность функции на промежутке. Свойства функций, непрерывных в точке

Точки разрыва функции и их классификация.