Задачник для самостоятельной работы студентов.
Задача 1: Составить уравнение прямой,
проходящей через точки
.
Ответ:
Задача 2: Дана прямая
.
Составить уравнение прямой, перпендикулярной
данной и походящей через точку M(-3;1)
Ответ:
Задача 3: Найти координаты точки M, делящей отрезок BC в отношении 1:5, если даны точки B (1;0) и С (5;8).
Ответ:
Задача 4: Найти координаты точки С, делящей отрезок AB в отношении 3:1, если A (8;1); B (0;4).
Ответ: С (-4;5,5)
Задача 5: Даны три последовательные вершины параллелограмма.
Найти
координаты четвёртой вершины
параллелограмма.
Ответ: D (7;-10)
Задача 6. Найти центр тяжести
Ответ:
Задача 7: На прямой, проходящей через точку A (-5;5) и В (-1;2) найти точку, абсцисса которой x=3.
Ответ: М (3;-1)
Задача 8: Доказать, что треугольник с вершинами А (1;2), В (5;-2), С(10;3) прямоугольный.
Задача 9: Дан треугольник с вершинами: А (-1;4), В (5;3), С (2;-1). Определить длины сторон этого треугольника.
Ответ:
Задача 10: Определить траекторию точки М, которая при свеем движении всё время остаётся вдвое ближе к точке А (0;1), чем к точке В (0;4).
Ответ: Окружность
с центром в начале координат.
Задача 11: Написать уравнение прямой, которая проходит через точку А (4;-3) и параллельна
а) оси абсцисс,
б) оси ординат,
в) прямой
Ответ: а) y=-3; б) x=4; в)2x-y-11=0
Задача 12:Написать уравнение прямой,
которая проходит через точку А (-2;3)
параллельно прямой
Ответ:
.
Задача 13: Написать уравнение
перпендикуляра, опущенного из точки
А (4;1) на прямую
Ответ:
Задача 14: Прямая проходит через середину отрезка АВ, где А (-2; 4), В (6;-8) и наклонна к оси ОХ под углом
.
Найти ее уравнение.
Ответ:
Задача 15: При каком значении параметра
прямые
;
перпендикулярны
друг другу?
Ответ:
Задача 16: Точки А (-4;1), В (5;2), С (1;3) являются вершинами треугольника. Написать уравнение высоты ВК.
Ответ:
Задача 17:Прямая
является одной из сторон прямоугольника
АВСD. Написать уравнения
сторон этого прямоугольника через
вершину А (-3;2).
Ответ:
;
Задача 18: Указать точку пересечения
прямой
и прямой
Ответ: М(-1;1)
Задача 19: В каком взаимном расположении находятся прямые:
19.1.
и
Ответ: параллельны.
19.2.
и
Ответ: пересекаются в точке А (2;3)
19.3.
и
Ответ: совпадают
19.4.
и
Ответ: перпендикулярны.
Задача 20.
Лежат ли на одной прямой три точки: А (-2;6); В (2;5); С (5;3).
Ответ: нет.
Тренировочная работа
Вариант 1.
1.Дана прямая
.
Указать координаты
.Построить
прямую.
2.указать точку пересечения прямых
и
.
Построить.
3.
.
Составить уравнение прямой и построить.
4.Указать точку пересечения прямой
и прямой
.
5. Дана прямая
.
Найти
,
к и b.
Ответы: 1.
.
2. А(4;-1). 3.
.
4. А (3;9). 5.
Вариант 2.
Построить:
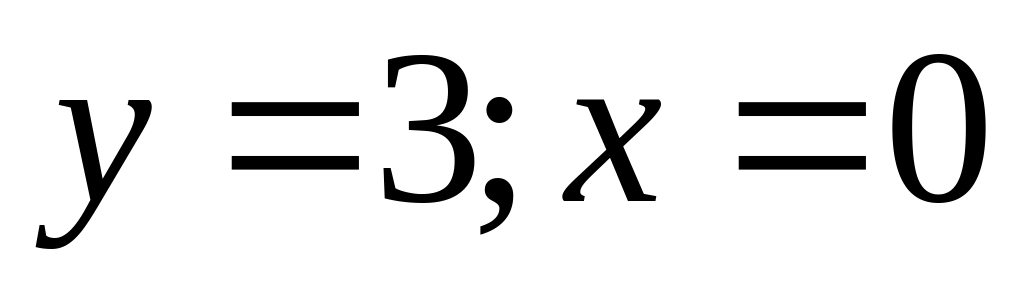.Дана прямая
.
Найти
,
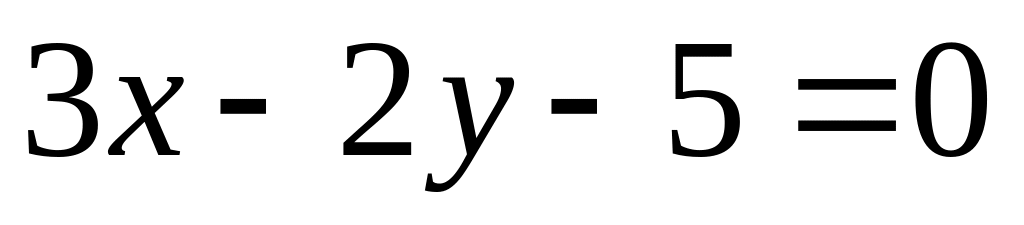к и b.Даны точки: М (3;0); N (2;1). Составить уравнение и построить.
Угол наклона прямой , начальная ордината
.
Составить уравнение и построить.Прямая
.
Найти координаты
.
Ответы: 1.
2.
.
3.
.
4.
или
5.
.
Вариант 3.
Указать координаты точки пересечения прямых x=4;
.
2.Дана прямая
.Найти
к и b.
3.Составить уравнение и построить линию по данным:
-
3.1.
М (1;0)
N(0;4)
3.2.
N (2; 0 )
M(2;-3)
4.Указать координаты точки пересечения
прямой
и
.
Построить.
Ответы: 1.(4;2). 2.
.
3. 1)
2)
4.(3;2)
Вариант 4.
Составить уравнение прямой и построить ее.
1.1.
1.2.
M (1;0)
N (0;4)
1.3.
n (0;1)
M(3;2)
Построить линии: y=-2; x=3.
Дана прямая 2x-3=0. Найти координаты
Ответы: 1)
1.2.
1.3.
3.
