Сергиенко Л.Ю.

Практическое пособие

по математике

по теме “Прямая

на плоскости

и ее уравнения”

Составитель Сергиенко Людмила Юльевна-

Преподаватель математики Санкт- петербургского технического колледжа управления и коммерции, кандидат педагогических наук, заслуженный учитель Р.Ф.

Рекомендации:

1. Романова Л.А. – преподаватель математики СПб ТКУ и К.

2. Рассмотрено и одобрено за заседании П(Ц)К естественно – математических дисциплин.

Протокол № 3 от 05.10.04

Председатель П(Ц)К Е.В.Фролова

Аннотация.

Практическое пособие по теме “Прямая на плоскости и её уравнения” составлено в соответствии с рабочими программами по математике. Практическое пособие рассчитано на студентов первого и второго курсов колледжа как технических, так и экономических специальностей. Пособие содержит большой объём материала для самостоятельной работы студентов. В пособии приведены 10 типовых задач с полным решением, 20 задач для самостоятельной работы и 65 – зачётных задач. Все задачи снабжены ответами. В пособии приведены краткие теоретические сведения. Пособие окажет помочь в систематизации и обобщении знаний и умений по теме.

Содержание:

1. Теоретические сведения……………………………….. 2. Решение типовых задач………………………………… 3. Задачник для самостоятельной работы студентов…… 4. Практическая работа…………………………………… 5. Зачётная работа по теме………………………………... 6. Литература по теме……………………………………...

1.Теоретические сведения.

1.1. Уравнение прямой, проходящей через данную точку, перпендикулярно заданному вектору.

Определение: Нормальным вектором прямо называется вектор перпендикулярный этой прямой.

3. т.к. , следовательно их скалярное произведение равно нулю, отсюда (1).

Раскроем скобки в формуле (1).

Обозначим: . Отсюда

(2)

Примечание:

В общем уравнении прямой:

,числа А и В являются координатами нормального вектора.

3. Уравнение прямой с угловым коэффициентом и начальной ординатой.

Определение: Угловым коэффициентом прямой называется тангенс угла наклона прямой к оси ОX.

Определение: Начальной ординатой прямой называется ордината точки пересечения прямой с осью OY.

Частные случаи:

1.3.1. то уравнение имеет вид x=m, следовательно: к- не существует, в- не существует.

1.3.2. то уравнение имеет вид y=m, при этом:

1.4 Связь уравнений вида:

и

Если ,то

1.5. Уравнение прямой, проходящей через данную точку и имеющей заданный угловой коэффициент.

1.5.1. Уравнение пучка прямых.

(9)

Примечания:

1. Формула (9) даёт уравнение пучка прямых, если к- неизвестен.

2. Формула (9) даёт уравнение единственной прямой, проходящей через т. , если к- заданная величина.

1. Уравнение прямой, проходящей через заданную точку в заданном направлении.

Определение: Направляющим вектором прямой называется ненулевой вектор, коллинеарный данной прямой.

(10) это уравнение называется каноническим

6. Уравнение прямой проходящей через две данные точки:

(11) где (x ;y) – координата любой точки прямой.

6. Уравнение прямой в отрезках.

1.9.Параметрические уравнение прямой.

Примем за параметр t величину, стоящую в правой и левой частях формулы (10), причём

Получим

или:

(13)

Это и есть искомые параметрические уравнения.

1.10.Определитель второго порядка.

Определение:

Определителем второго порядка называется выражение

(14)

11. Нахождение координат точки пересечения двух прямых.

Если две непараллельные прямые заданы своими уравнениями:

, то координаты точки

Пересечения этих прямых – есть решение системы уравнений.

Чтобы найти точку пересечения прямых нужно составить три

определителя системы и найти значения переменных . Если главный определитель системы , то система имеет единственное решение.

1.12.Угол между прямыми .

Угол между двумя прямыми, заданными общими уравнениями:

и вычисляется по формуле:

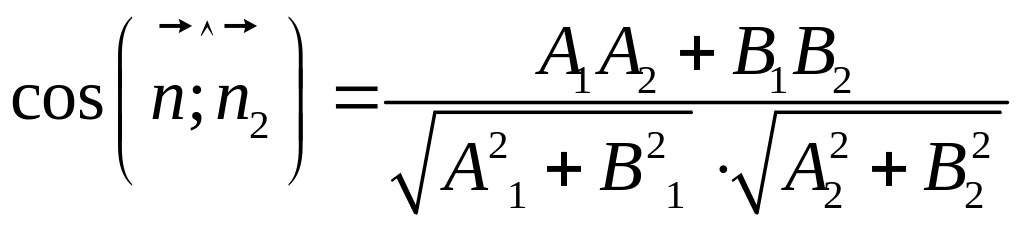(15).

Угол между двумя прямыми, заданными уравнениями:

и .Вычисляется по формуле :

(16).

Угол между двумя прямыми, заданными каноническими уравнениями:

и вычисляется по формуле:

(17).

Примечание: Формула (15),(16),(17) могут дать значение тригонометрической функции одного из двух углов (острого или тупого) между заданными прямыми. Для нахождения острого угла, результат вычислений берут по модулю.

Частные случаи:

1.12.1. Условие параллельности двух прямых:

(18)

где и - угловые коэффициенты прямых .

Если две прямые представлены уравнениями:

и если

то прямые - параллельны.

Условие параллельности прямых является пропорциональность коэффициентов переменных. Если свободные члены уравнений пропорциональны:

, то прямые совпадают.

1.12.2. Условие перпендикулярности двух прямых:

(19)

где - угловые коэффициенты прямых.

Если две прямые представлены уравнениями:

то условие их перпендикулярности:

(20)

т.е. их скалярное произведение равно нулю.

1.13 Нахождение длины отрезка:

(21)

где точка

14. Деление отрезка в данном отношении

(22)

где - начало отрезка,

- конец отрезка

В этом случаи точки M делит отрезок AB во внешнем отношении.

Если , то точка M – середина отрезка.

(23)

14. Расстояние от точки K до прямой

, определяется по формуле:

(24)

16. Центр тяжести треугольника находится в точке

, где вершина

(25)

16. Площадь треугольника.

Точки - вершины треугольника.

Площадь треугольника вычисляется по формуле:

(26)

Площадь треугольника – величина положительная. Поэтому перед определителем ставим знак плюс, если его значение – положительное число и знак минус, если его величина – число.

Частный случай: Если вершина совпадают с началом координат, то площадь треугольника вычисляется по формуле:

(27)