Теорема
Ранг
ступенчатой матрицы равен числу её
ненулевых строк, причём 0
.
Пример. Найти ранг матрицы методом элементарных преобразований.
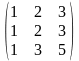
Заметим,
что матрицу с помощью элементарных
преобразований можно привести к виду,
когда все её элементы, кроме элементов
,
равны 0. Тогда ранг матрицы будет равен
r.
Системы линейных уравнений (СЛУ)
Система m линейных уравнений с n неизвестными имеет вид
,
где
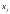– неизвестные,
– коэффициенты при неизвестных, а
– свободные члены.
Решить СЛУ, значит найти множество её решений. Оно может быть пустым, конечным или бесконечным.
Решением СЛУ называется упорядоченная совокупность из чисел, компоненты которой удовлетворяют каждому уравнению системы.
СЛУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более 1 решения.
В случае неопределённой системы, каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решение СЛУ
Формулы Крамера (Габриель Крамер (1704-1752) швейцарский математик).
Пусть дана система n линейных уравнений с n неизвестными.
Составим
матрицы: A
=
;
B
=
;
X
=
.
Если
определитель системы
,
составленный из коэффициентов при
неизвестных отличен от 0, то система
имеет единственное решение.
Систему уравнений можно записать:
AX = B.
Сделаем следующее преобразование: A-1AX = A-1B.
Т.к. А-1А = Е, то ЕХ = А-1В ,
Х = А-1В – решение с помощью обратной матрицы или
– формулы
Крамера,
где
– определители, полученные из определителя
заменой в нём i-го
столбца столбцом из свободных членов
.
Пример.
A
=
;
1=
;
2=
;
3=
.
x1 = 1/detA; x2 = 2/detA; x3 = 3/detA.
Метод Гаусса (Карл Фридрих Гаусс (1777-1855) немецкий математик).
Пусть
дана система
линейных уравнений с
неизвестными.
Составим матрицы:
А
=
называется матрицей системы и матрица
А*=
называется расширенной матрицей системы.
Теорема Кронекера-Капелли (критерий совместности системы линейных уравнений).
Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Расширенная
матрица системы
с помощью
элементарных преобразований строк
приводится к ступенчатому виду. При
этом возможны случаи:
r(A)= r( )=r =n, что соответствует системе, которая имеет единственное решение.
Неизвестные при этом находятся последовательно, начиная с последнего уравнения.
r(A)= r( )= r
n,
что соответствует системе, которая
имеет бесконечно много решений.
В этом случае выбираются главные неизвестные (их количество определяется рангом) и свободные (их количество n-r). Затем главные неизвестные выражаются через свободные, начиная с последнего уравнения. Свободные неизвестные могут принимать любые значения, что даёт общее решение системы.
Пример. Решить систему методом Гаусса.
.
Составим расширенную матрицу системы.
Таким образом, исходная система может быть представлена в виде:
,
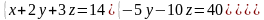откуда получаем: z
= 3; y
= 2; x
= 1.
Если b1, b2, …,bm = 0, то система называется однородной. Однородная система всегда совместна.