Махнева Т.В., ФАМ, 2015

Линейная алгебра

Матрицы. Определители

Матрицей размерности mn называется прямоугольная таблица из m строк и n столбцов, составленная из чисел или иных математических выражений. Элементы матрицы обозначаются , где i- номер строки, а j- номер столбца.

А =

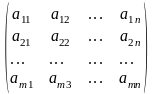
Матрица, все элементы которой равны 0, называется нулевой и обозначается О.

Если , то матрица называется квадратной порядка .

Квадратная матрица, все элементы которой, кроме элементов главной диагонали ( ), равны 0, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен 1, называется единичной и обозначается .

Всякой квадратной матрице порядка можно поставить в соответствие её определитель (детерминант).

Определителем квадратной матрицы А= n-го порядка называется выражение (число), полученное по определенному правилу.

Определитель 1-го порядка (n=1) равен самому элементу: .

Определитель 2-го порядка (n=2): .

Определитель 3-го порядка (n=3): .

и т.д. Определители обозначаются символом или .

Если , то матрица называется вырожденной (невырожденной).

Две матрицы A и B одинаковой размерности называются равными, если равны элементы, стоящие на одинаковых местах, т.е. .

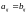Свойства определителей

1. Определитель не изменится, если в нем каждую строку заменить столбцом с соответствующим номером (транспонирование определителя). Следовательно, строки и столбцы в определителе равноправны, т.е. любое свойство (теорема), относящееся к строкам определителя, справедливо и для его столбцов.

2. Если в определителе все элементы какой-либо строки равны 0, то определитель равен 0.

3. Если в определителе 2 строки поменять местами, то определитель изменит знак на противоположный.

4. Если определитель содержит 2 одинаковые строки, то он равен 0. Действительно, при перестановке одинаковых строк, с одной стороны, определитель не изменится, с другой стороны, изменит знак на противоположный. Т.о., , 2 ,

5. Общий множитель элементов какой-либо строки определителя можно выносить за знак определителя.

6. Если элементы какой-либо строки определителя представляют сумму 2-х слагаемых, то определитель равен сумме 2-х соответствующих определителей.

7. Определитель не изменится, если к элементам какой-либо строки определителя прибавить элементы другой строки, умноженные на некоторое число.

Миноры и алгебраические дополнения

Минором элемента определителя n-го порядка называется такой определитель (n-1)-го порядка, который получается из определителя n-го порядка вычеркиванием i-ой строки и j-го столбца.

Алгебраическим дополнением 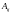элемента называется его минор, взятый со знаком , т.е. .

Теорема Лапласа (о разложении определителя).

Определитель n-го порядка равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения: (разложение определителя по элементам i-ой строки).

Пример. Вычислить определитель матрицы А = .

Для по теореме Лапласа:

= -5 + 18 + 6 = 19.

Аналогичное разложение можно записать для элементов -го столбца.

На теореме основан метод вычисления определителей понижением их порядка. Если в определителе n-го порядка все элементы i-ой строки, за исключением одного, равны 0, то такой определитель равен этому отличному от 0 элементу, умноженному на его алгебраическое дополнение.

Для вычисления определителей n-го порядка также используется метод приведения к треугольному виду, когда все элементы, расположенные выше (ниже) одной из его диагоналей равны 0.

Для преобразования определителя к соответствующему виду используются свойства определителя.