2.2.Конкурирующие точки

Определение: точки, лежащие на одной прямой, перпендикулярной какой-либо плоскости проекций (рис.9). Они конкурируют в видимости на той плоскости проекций, к которой ортогональна проецирующая прямая.

Признак: проекции конкурирующих точек проекции совпадают в той плоскости, в которой они конкурируют в видимости(рис.9, 9а).

Для определения видимости точек на чертеже рассматриваются их проекции совместно с направлением взгляда на плоскость конкуренции.

Задача. Построить чертеж точки А (40,20,30) и горизонтально конкурирующую с ней точку В и видимую на П₁. (рис.10).

Алгоритм решения:

1. Строим проекции точки А₁₂ А₂₃ А₁₃ на осях проекций, откладывая соответствующей длины координатные отрезки.

2. Через построенные проекции проводим линии связи, перпенди-кулярные осям, на которых эти проекции расположены.

3. В точках пересечения линий связи отмечаем проекции точки А на плоскостях проекций А₁, А₂ и А_3.

4. Строим проекции точки В :

   • т.к. А и В – горизонтально конкурирующие, то А₁=В₁;

   • т.к. В видима на П₁, то она ближе расположена к наблюдателю , чем точка А, и имеет большую высоту.

3. Чертеж прямой

В пространстве прямая задаётся двумя своими точками или точкой и направлением. На чертеже прямая задается своими проекциями: либо проекциями отрезка, либо участка прямой без указания ей принадлежащих точек (рис.11).

На чертеже прямой l не указаны ни ли-нии связи, ни ось проекций (безосный чертеж). В случае необходимости ось может быть про-ведена в любом месте чертежа при одном усло-вии – она должна быть горизонтальна.

3.1.Положение прямой относительно плоскостей проекций

3.1.1.Прямая общего положения.

Определение: наклонена ко всем плоскостям проекций(рис.12).

Признак: проекции прямой наклонены к осям проекций (рис.11).

Свойства чертежа: отрезок прямой и углы наклона прямой к плоскостям проекций проецируются на плоскости проекций с искажением. Восходящей называется прямая, высота точек которой возрастает по мере удаления от наблюдателя, у нисходящей - уменьшается.

Признак: у восходящей прямой проекции наклонены в одну сторону ( l на рис.11), у нисходящей - в разные (АВ на рис.11).

Для определения на чер-теже натуральной величины (НВ) отрезка прямой общего положения и углов наклона её к плоскостям проекций применяется метод прямоугольного треугольника.

На наглядном изображении отрезка АВ (рис.12) проведем АК А₁В₁. Из прямоугольного треугольника АКВ следует, что натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, один катет которого равен проекции отрезка в горизонтальную плоскость проекций, а другой катет – разности высот концов отрезка АВ. Угол треугольника между АВ и проекцией отрезка есть НВ угла наклона прямой к П₁.

В общем случае:

натуральная величина отрезка прямой общего положения равна гипотенузе пря-моугольного треугольника, один катет которого равен проекции отрезка в какую-либо плоскость проекций, а другой - разности удалений концов отрезка от той же плоскости проекций, на которой взят первый катет треугольника. Чтобы определить угол наклона прямой к какой-либо плоскости проекций, при построении прямоугольного треугольника в качестве первого катета нужно взять проекцию отрезка в эту плоскость.

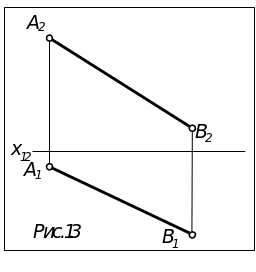Задача. Определить НВ отрезка АВ и угла наклона его к П₂ (рис.13)_.

Алгоритм решения

1. Т.к. АВ – отрезок общего положения, то для решения применяем метод прямоугольного треугольника.

2. Т.к. нужно определить угол наклона к П₂, то при по-строении прямоугольного треугольника в качестве первого катета берем фронтальную проекцию А₂В₂.

3. Из В₂ (можно из А₂) проводим перпендикуляр к А₂В₂ и в качестве второго катета откладываем разность глубин концов отрезка f.

А₂В₀ – натуральная величина отрезка,  - угол на­клона его к П₂.

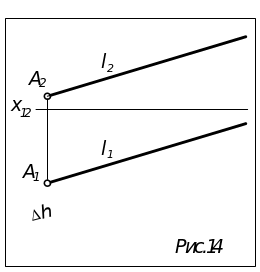Задача. На прямой l отложить отрезок АВ = 40 мм (рис.14).

Алгоритм решения

1. Т.к. прямая l – общего положения, отложить от точки А отрезок, равный 40мм нельзя: на прямой общего положения отрезки проецируются с искажением.

2. Чтобы построить такой отрезок применяем метод пря-моугольного треугольника: берем на прямой l произ-вольную точку С и определяем НВ отрезка АС, взяв в качестве первого катета его горизонтальную проекцию, а в качестве второго - разность высот его концов. На построенной НВ отрезка АС откладываем от А₀ нужную длину.

3. Из построенной точки В₀ опускаем перпендикуляр на l₁ и находим горизонтальную проекцию точки В₁, а по принадлежности l и её фронтальную проекцию . Отрезок АВ имеет нужную длину.