Лабораторная работа № 1

Исследование методов решение простых задач

Цель занятия:

• Совершенствование навыков разработки программ в среде программирования MS Visual C++

• Исследование диапазонов представимости числовой информации стандартными типами данных

• Исследование допустимых преобразований типов данных в языке Си

Время на выполнение работы: 2 часа

Программа исследований:

1. Формализация задачи

2. Составление алгоритма решения

3. Написание программного кода

4. Отладка и тестирование программы

Подготовка к выполнению работы:

1. Изучить материал настоящего руководства и рекомендованную литературу (структура программы на языке высокого уровня, алфавит и элементарные конструкции языка С++, переменные и константы, стандартные типы данных).

2. Практически освоить порядок работы на ПЭВМ в среде программирования Visual C++.

Материалы для подготовки к занятию:

1. Конспект лекций

2. [1] стр. 22-26

3. [2] стр. 48-91

Методические рекомендации

Задача 1. Координаты брошенного под углом тела

Рассмотрим программу, в которой вычисляются координаты тела, брошенного под углом к горизонту. Если телу в начальный момент сообщена скорость v и тело брошено под углом α к горизонту, то зависимость x-координаты от времени t дается соотношением . Для у-координаты закон движения имеет вид 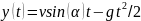, где 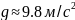есть ускорение свободного падения. Время полета тела до падения составляет . В программе вводится значение скорости тела и угол, под которым тело брошено к горизонту. Угол вводится в градусах, поэтому вводимое значение переводится в радианы (умножается на и делится на 180). Далее вычисляется время полета тела, и пользователю предлагается ввести момент времени (не превышающий время полета тела), для которого необходимо рассчитать координаты тела. Эти координаты выводятся на экран. Код программы приведен в листинге 1.

Листинг 1. Тело брошено под углом к горизонту

Для использования встроенных математических функций в блок заголовков включена команда #include <math.h>. Результат выполнения программы может выглядеть следующим образом (жирным шрифтом выделены данные, вводимые пользователем):

В программах такого типа разумнее предусматривать возможность вычисления координат для разных моментов времени. Делается это с помощью условных операторов и операторов цикла.

Задача 2. Средняя скорость движения мотоциклиста

Решим задачу о вычислении средней скорости движения мотоциклиста на участке от пункта А до В через пункт Б, если расстояние между пунктами А и Б составляет , а расстояние между пунктами Б и В равно S₂. Время движения мотоциклиста между пунктами А и Б равно , а время движения между пунктами Б и В равно Средняя скорость определяется как Параметры S₁, S₂, t₁ и t₂ вводятся пользователем с клавиатуры. Программный код приведен в листинге 2.

Листинг 2. Средняя скорость мотоциклиста

Результат выполнения программы может выглядеть следующим образом:

Выше предполагалось, что расстояние вводится в километрах, а время - в часах.

Задача 3. Высота орбиты спутника

В следующей задаче необходимо определить высоту орбиты спутника h над поверхностью Земли, если известны масса 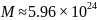(кг) и радиус (м) Земли, масса спутника т, период его обращения Т. Масса спутника в данном случае при расчете высоты орбиты не нужна, а период обращения вводится пользователем.

При решении этой задачи воспользуемся тем, что сила гравитационного притяжения между Землей и спутником равна где (Нм²/кг²) - универсальная гравитационная постоянная. С другой стороны, эту же силу по второму закону Ньютона можно записать как где есть центростремительное ускорение, а частота связана с периодом Т соотношением . Из этих соотношений получаем , что дает . Соответствующий программный код приведен в листинге 3.

Листинг 3. Высота орбиты спутника

Продолжение листинга 3

Результат выполнения программы может выглядеть следующим образом:

В программе использована встроенная функция pow() для вычисления кубического корня. Первым аргументом функции указывается возводимое в степень выражение, второй ее аргумент - степень, в которую возводится выражение. В данном случае степень равна 1/3. Однако в силу автоматического преобразования типов при вычислении выражения 1/3 используется целочисленное деление, в результате чего получаем 0. Чтобы избежать такой неприятности, во втором аргументе функции pow() использована инструкция (double) для выполнения явного приведения типов.

Обратите внимание на способ ввода больших чисел: они вводятся в формате мантиссы и показателя степени. Например, число (литерал) вводится как 6.672Е-11, а число – как 5.96Е24.