Вариант 2

1. Найти наибольшее и наименьшее значение функции

Z= x²+4xy-y²-6x-2y

в замкнутом треугольнике, ограниченном осями координат и прямой 2x + 3y – 6 = 0

2. Изменить порядок интегрирования в двойном интеграле

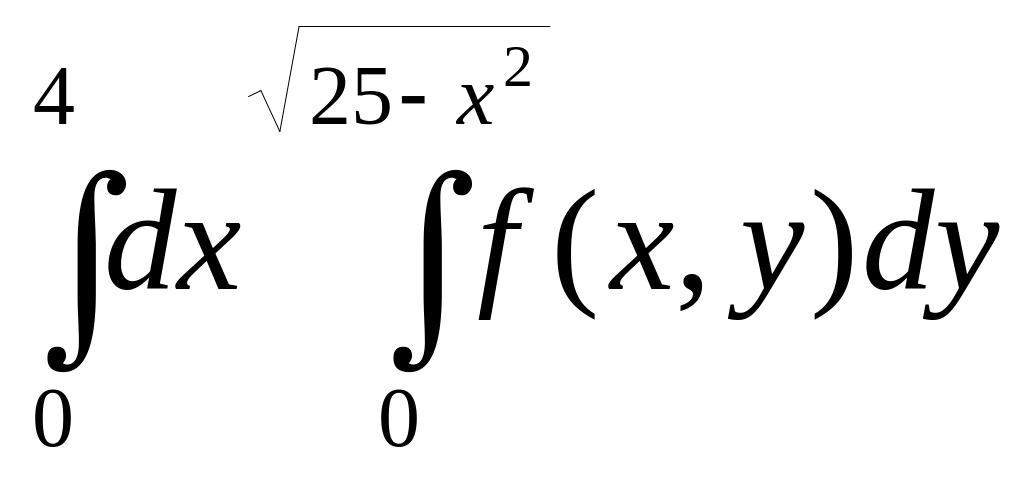
Сделать чертеж области интегрирования.

3. Найти массу тела, ограниченного плоскостью z = 0, цилиндром x²+y²=R² и конусом z= 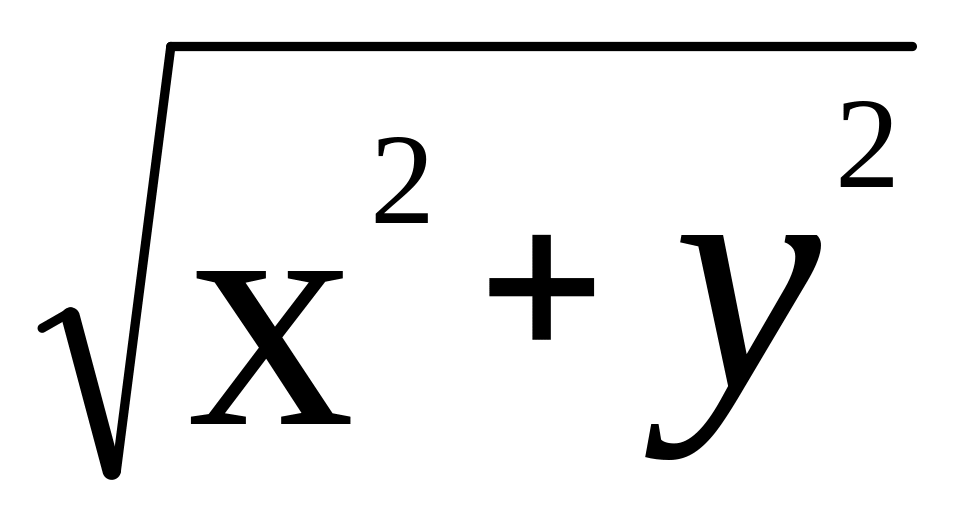, если плотность в каждой его точке численно равна расстоянию от этой точки до оси oz.

4. Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U с помощью криволинейного интеграла

(sin²y-ysin2x) dx + (xsin2y+cos²x+1) dy

5. Найти циркуляцию векторного поля по контуру 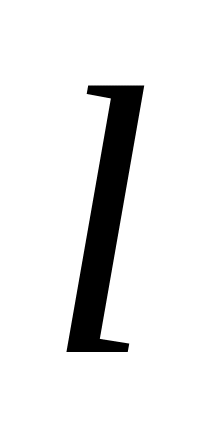. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя интеграл векторного поля по контуру £; б) по теореме Стокса

:

Вариант 3

1. Найти наибольшее и наименьшее значения функции

Z=x²+2xy-y²-4x в треугольниками со сторонами y=x+1, y=0,x=3

2. Изменить порядок интегрирования в двойном интеграле

Сделать чертеж области интегрировании

3. Найти координаты центра тяжести однородного тела, ограниченного параболоидом x² + 4z² = 4y и плоскостью y = 2

4. Вычислить криволинейный интеграл 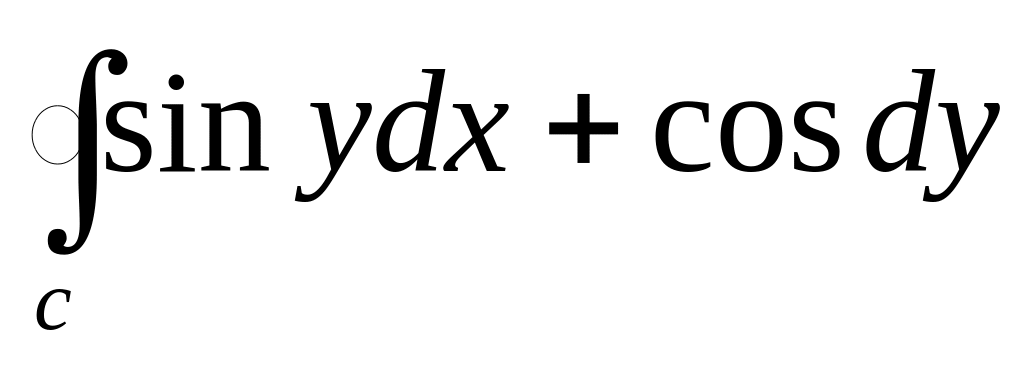по замкнутому контуру С = ОАВО; где О-начало координат;ОА-отрезок оси ОХ; ВО- отрезок оси ОУ; линия АВ дана уравнением

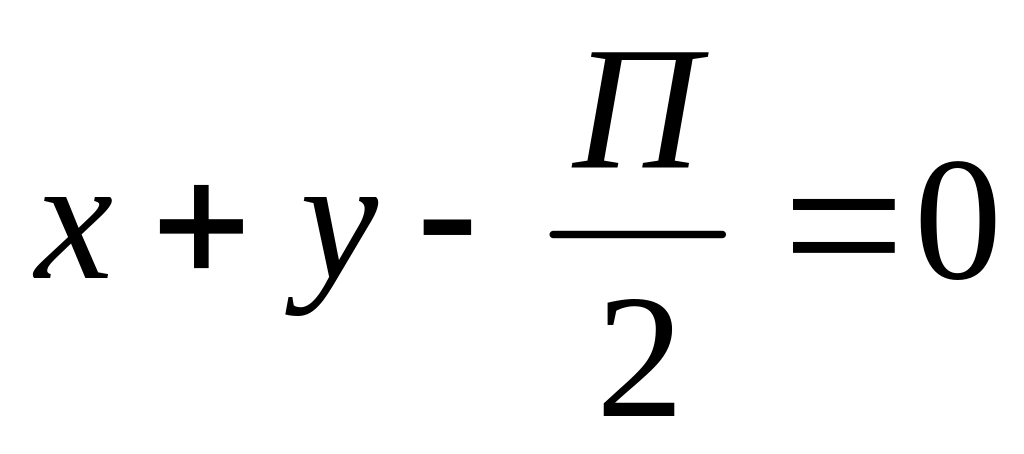
Вычисление провести двумя способами: непосредственно и по формуле Грина

5. Вычислить поток поля вектора через треугольник, вырезанный из плоскости x+y+2z-2=0 координатными плоскостями, в том направлении к плоскости, которое образует с осью ОУ острый угол

Вариант 4

1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г

Z=x²-2xy-y²-4x; T: y=x+1, y=0, x=3

2. Изменить порядок интегрирования в двойном интеграле

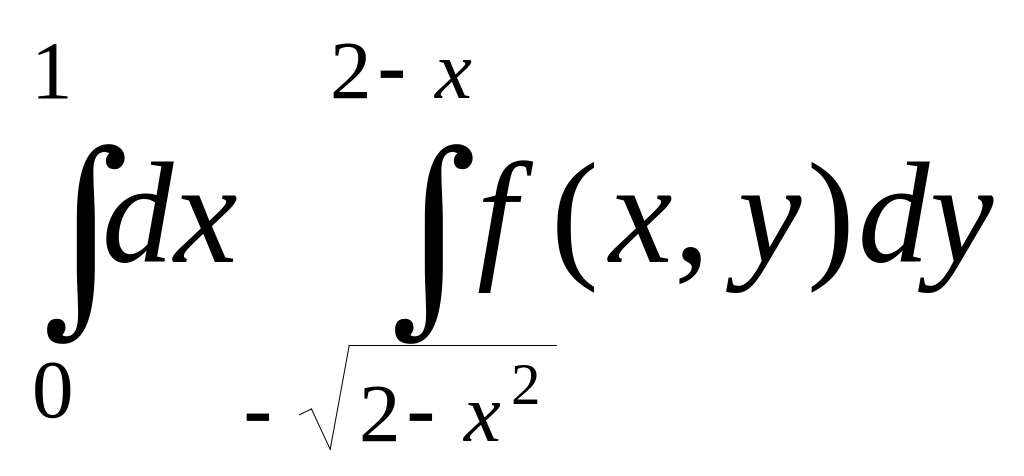
Сделать чертеж области интегрирования.

3. Найти центр тяжести однородного тела, ограниченного поверхностями: x=0, y=0, z=0, x+y+z=8

4. Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.

5. Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса

F:

Вариант 5

1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г

Z=x²-2xy-2y²-4x+6y+3

2. Изменить порядок интегрирования в двойном интеграле

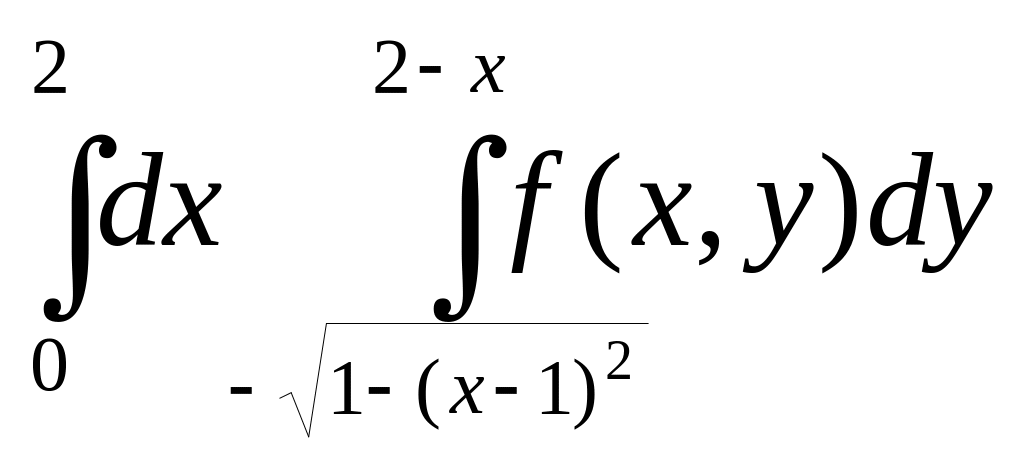
Сделать чертеж области интегрирования

3. Найти центр тяжести однородного тела, ограниченного плоскостями x = 0, y = 0, z = 0, 6x+3y+2z-6=0

4. Поверить, является ли заданное выражение дифференциалом некоторой функции (x,y) и в случае положительного ответа найти И(x,y) с помощью криволинейного интеграла.

5.Найти циркуляцию векторного поля по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисление провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса

Г: (1-ый октант)