1.3. Исчисление высказываний

Логическим исчислением, или просто исчислением, называется формальная система, в которой определены алфавит, правила построения формул, некоторое множество аксиом и правил вывода. Аксиомы и правила вывода позволяют строить новые формулы, которые являются общезначимыми, т.е. также являются аксиомами или теоремами. Правила вывода применяются непосредственно к формулам, а не к таблицам истинности. Исчисление высказываний может включать много аксиом и мало правил вывода, тогда оно образует аксиоматическую формальную систему или классическое исчисление высказываний.

1.3.1. Классическое исчисление высказываний

Логика высказываний может быть представлена как аксиоматическая система с логическими аксиомами и правилами вывода. Аксиомы – это некоторые тавтологии, а правило вывода R выводит высказывание  из последовательности высказываний

Исторически первой аксиоматической системой классической логики была система, предложенная Г. Фреге, содержащая пять аксиом:

1. ├

2. ├

3. ├

4. ├

5. ├ ├

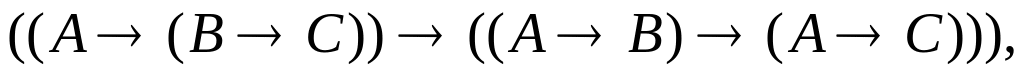
Позднее Я Лукасевич уменьшил число аксиом в системе Фреге до трех. Схемами аксиом являются следующие схемы формул:

- утверждение посылки;

- самодистрибутивность ;

- контрапозиция.

Система аксиом логики высказываний:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

Все аксиомы включают только пропозициональные переменные и истинны в любой интерпретации. Поэтому если удается достаточно адекватно интерпретировать эти аксиомы в какой-либо среде, то аксиоматическая теория может служить основой для рассуждений об этой среде. Из этой системы аксиом можно получить неограниченное число аксиом. Легко проверить, что все аксиомы являются правильно построенными формулами языка логики высказываний и, конечно, тавтологиями.

Классическое исчисление высказываний использует два правила вывода:

1. Modus Ponens (MP), которое констатирует тот факт, что из истинности импликации и ее посылки следует истинность заключения импликации, записывается следующим образом: () ├  . Символ ├ обозначает выводимость в аксиоматической системе. Иначе это правило записывается так: 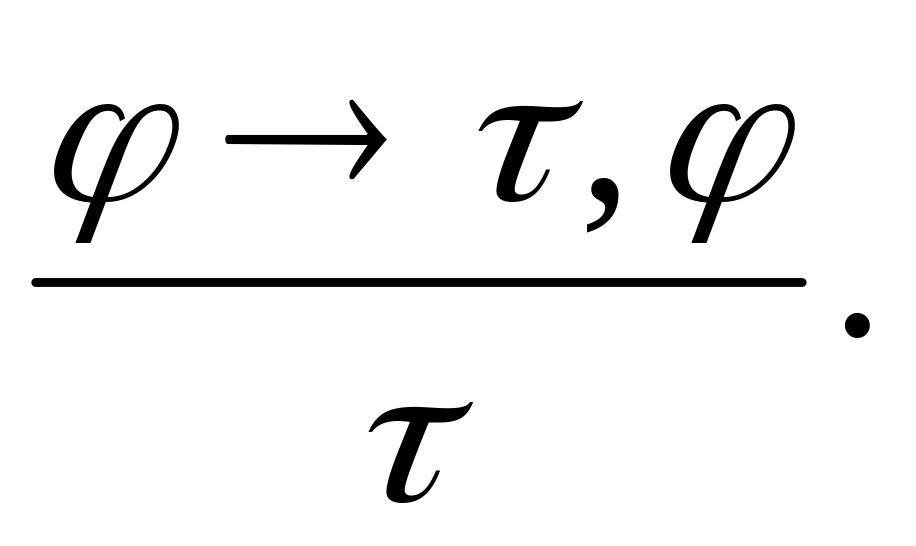В этой записи ,  – формулы; формулы, записанные над чертой, означают истинные посылки правила (т.е. установлены как теоремы), а формула под чертой – следствие из этих посылок, которое также является теоремой.

• Правило подстановки имеет вид

.

Здесь , q_i, i суть формулы, x_i, i попарно различные пропозициональные переменные. Правило означает результат одновременного замещения всех вхождений букв x_i в формуле  на формулы q_i соответственно. Если пропозициональная переменная x_i не входит в формулу , то соответствующая формула q_i никуда не подставляется и просто не играет никакой роли.

Опишем теперь, что является теоремой, или выводимой формулой теории L.

Дадим индуктивное определение доказательства высказывания аксиоматическим методом.

Пусть S – множество высказываний.

1. Доказательством (выводом) из S называется такая конечная последовательность высказываний , что верно, если

1. _i S или

2. _i – аксиома или

3. _i получено из _j, _k, где 1j, ki, по правилу Modus Ponens.

2. Высказывание _n называется доказуемым (выводимым) из множества высказываний S, если существует такое доказательство 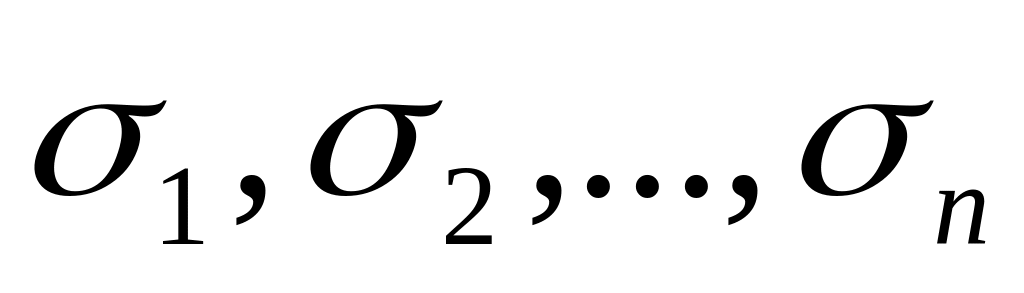из S, что _n совпадает с . Выводимость высказывания  из множества высказываний S обозначается: S├.

3. Высказывание  называется доказуемым (выводимым), если ├ , т.е. выводимо в аксиоматической системе при помощи правила Modus Ponens.

4. Теоремой является любое высказывание, присутствующее в доказательстве.

Докажем, что ├ (АА).

Из аксиомы А1 получим

├ (А((ВА)А))	(1)
Вторую аксиому запишем в виде:
├ (А((BА)А)(((А(ВА))(АА)).	(2)
Из (1) и (2) по правилу Modus Ponens, получаем, что
├ (А(ВА))(АА).	(3)
Вновь используя аксиому А1 и правило Modus Ponens, заключаем, что
├ (АА). Следовательно, высказывание (АА) выводимо в нашей аксиоматической системеi.

Покажем, что в рассматриваемой интерпретации всякая выводимая формула исчисления высказываний есть тавтология. Для этого надо проверить, что все аксиомы 111тавтологии. Такая проверка проводится элементарно построением таблиц истинности. Далее всякая выводимая формула является конечной формулой некоторого вывода. Выводом является последовательность формул, в которой каждая предыдущая формула является аксиомой или получена из предыдущих формул с использованием правил modus ponens и подстановки. Поэтому достаточно проверить, являются ли получаемые формулы тавтологиями. Такая проверка тривиальна. Следовательно, любая выводимая формулатавтология.

Имеет место и обратное утверждение: в исчислении высказываний всякая тавтология выводима.