4.3 Числовые последовательности
1. Числовые последовательности и операции над ними
Определение. Если каждому натуральному
числу
поставлено в соответствие по некоторому
закону
определённое число
,
то говорят, что на множестве всех
натуральных чисел
задана последовательность
Общий член последовательности является функцией от .
Таким образом, последовательность является функцией натурального аргумента.
Задать последовательность можно различными способами. Необходимо только, чтобы был указан способ получения любого члена последовательности.
Пример.
или
.
или
Для последовательностей можно определить следующие операции:
Умножение последовательности на число :
,
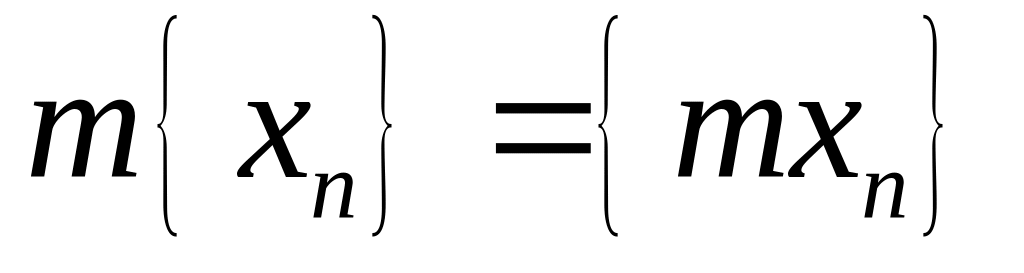т.е.
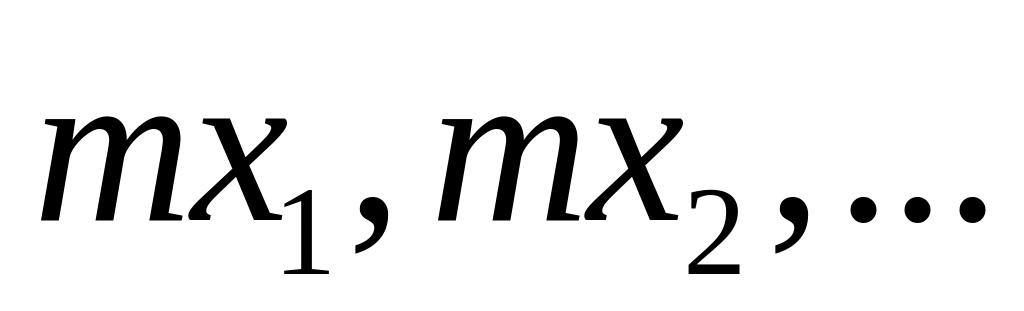
Сложение (вычитание) последовательностей:
.Произведение последовательностей:
.Частное последовательностей:
при
.
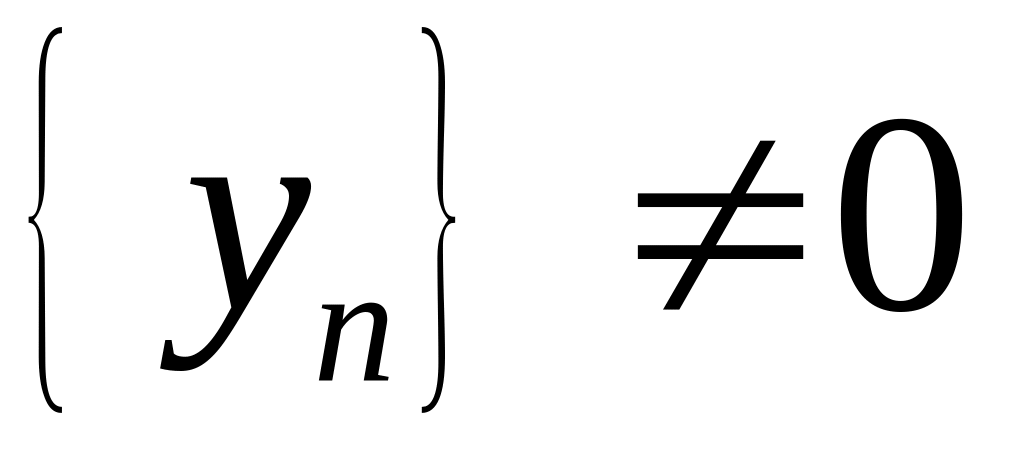2. Ограниченные и неограниченные последовательности
Определение. Последовательность
называется ограниченной, если
существует такое число
,
что для любого
справедливо неравенство:
т.е. все члены
последовательности принадлежат отрезку
.
Определение. Последовательность называется ограниченной сверху, если для любого существует такое число , что
.
Определение. Последовательность называется ограниченной снизу, если для любого n существует такое число , что
Пример.
– ограничена снизу {1, 2, 3, … }.
Определение. Число
называется пределом последовательности
,
если для любого положительного
существует такой номер
,
что для всех
выполняется неравенство:
Обозначение:
.
В этом случае говорят, что последовательность
сходится к
при
.
Пример.
Доказать, что предел последовательности
.
Пусть при
верно
,
т.е.
.
Это верно при
,
таким образом, если за
взять целую часть от
,
то утверждение, приведенное выше,
выполняется.
Пример. Показать, что при
последовательность
имеет пределом число 2. Имеем
;
.Для
любого положительного числа
существует такое натуральное число
,
что
,
т.е.
.
Теорема. Последовательность не может иметь более одного предела.
Доказательство. Предположим, что
последовательность
имеет два предела
и
,
не равные друг другу.
.
Тогда по определению существует такое число , что
и
.
Запишем
выражение:
.
Так как
-
любое положительное число, то
,
т.е.
.
Теорема доказана.
Теорема. Если
,
то
.
Доказательство. Из
следует, что
.
В то же время:
,
т.е.
, т.е.
.
Теорема доказана.
Теорема. Если , то последовательность ограничена.
Необходимо отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.
Например,
последовательность
не
имеет предел. В то же время
3. Монотонные последовательности
Определении
1) Если
для всех
,
то последовательность называется
возрастающей.
2) Если
для всех
,
то последовательность называется
неубывающей.
3) Если
для всех
,
то последовательность называется
убывающей.
4) Если
для всех
,
то последовательность называется
невозрастающей.
Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.
Пример.
– убывающая и ограниченная;
– возрастающая и неограниченная.
Пример. Доказать, что последовательность
монотонная и возрастающая.
Найдем
-й
член последовательности
Найдем знак разности:
,
т.к.
,
то знаменатель положительный при любом
.
Таким образом, . Последовательность возрастающая, что и следовало доказать.
Пример. Выяснить является возрастающей или убывающей последовательность
.
Найдём
.
Определим разность
,
так как
,
то
,
т.е.
.
Последовательность монотонно убывает.
Заметим, что монотонные последовательности являютс ограниченными по крайней мере с одной стороны.
Теорема. Монотонная ограниченная последовательность имеет конечный предел.
Доказательство. Рассмотрим монотонную неубывающую последовательность
Эта последовательность ограничена
сверху:
,
где
– некоторое число. Так как любое
ограниченное сверху, числовое множество
имеет точную верхнюю грань, то для любого
существует число
такое, что
,
где
– точная верхняя грань множества
значений последовательности.
Так как
-
неубывающая последовательность, то при
,
.
Отсюда
или
или
,
т.е.
.
Для остальных монотонных последовательностей доказательство аналогично. Теорема доказана.