4.2 Непрерывность функции

1. Непрерывность функции в точке

Определение. Функция , определенная в некоторой окрестности точки , называется непрерывной в точке , если предел функции и ее значение в этой точке равны:

Тот же факт можно записать иначе: .

Определение. Если функция определена в некоторой окрестности точки , но не является непрерывной в самой точке , то она называется разрывной функцией в этой, а сама точка называется точкой разрыва этой функции.

Пример непрерывной функции:

y

x

Пример разрывной функции:

y

x

Определение. Функция называется непрерывной в точке , если для любого положительного числа существует такое число , что для любых , удовлетворяющих условию

,

выполняется неравенство

.

Определение. Функция называется непрерывной в точке , если приращение функции в точке является величиной бесконечно малой в этой точке:

где – функция бесконечно малая при .

Если функция непрерывна в каждой точке множества , то говорят, что она непрерывна на множестве .

Непрерывная функция изображается на графике непрерывной кривой.

2. Свойства непрерывных функций

1) Сумма, разность и произведение непрерывных в точке функций – есть функция, непрерывная в точке .

2) Частное двух непрерывных функций – есть функция, непрерывная в точке , при условии, что не равна нулю в точке .

3) Композиция непрерывных в некоторой точке функций – есть функция непрерывная в этой точке

Это свойство может быть записано следующим образом:

Если , – непрерывные функции в точке , то функция – также непрерывная в этой точке.

Справедливость приведенных выше свойств можно доказать, используя теоремы о пределах функции в точке.

3. Непрерывность некоторых элементарных функций

1) Функция , – непрерывная функция на всей области определения.

2) Рациональная функц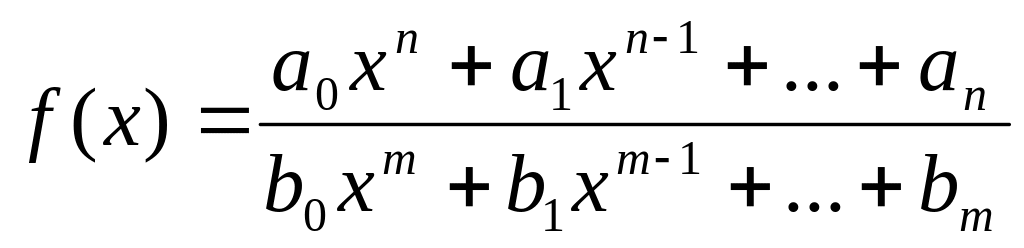ия непрерывна для всех значений , кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

3) Тригонометрические функции и непрерывны на своей области определения.

Докажем свойство 3) для функции .

Запишем приращение функции

, или .

Тогда

.

Действительно, рассмотрим предел произведения двух функций и . Функция косинус – ограниченная функция при , а так как

предел функции синус , то она является бесконечно малой при .

Таким образом, имеем произведение ограниченной функции на бесконечно малую. Следовательно, это произведение, т.е. функция – бесконечно малая. В соответствии с рассмотренными выше определениями, функция – непрерывная функция для любого значения из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.