16. Раскрытие неопределенностей

К разряду неопределенностей принято относить следующие соотношения:

.

Теорема (правило Лопиталя). Если функции и дифференцируемы в некоторой окрестности точки а, непрерывны в точке а, отлична от нуля в некотоой окретности точки а и , то предел отношения функций при равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

Доказательство. Применив формулу Коши, получим:

,

где - точка, находящаяся между и . Учитывая, что , находим

.

Пусть при отношение стремится к некоторому пределу. Так как точка лежит между точками и , то при получим и, следовательно, отношение стремится к тому же пределу. Таким образом:

.

Теорема доказана.

Пример. Найти предел .

Как видно, при попытке непосредственного вычисления предела получается неопределенность вида . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя. Находим

; ;

.

Пример. Найти предел .

; ;

.

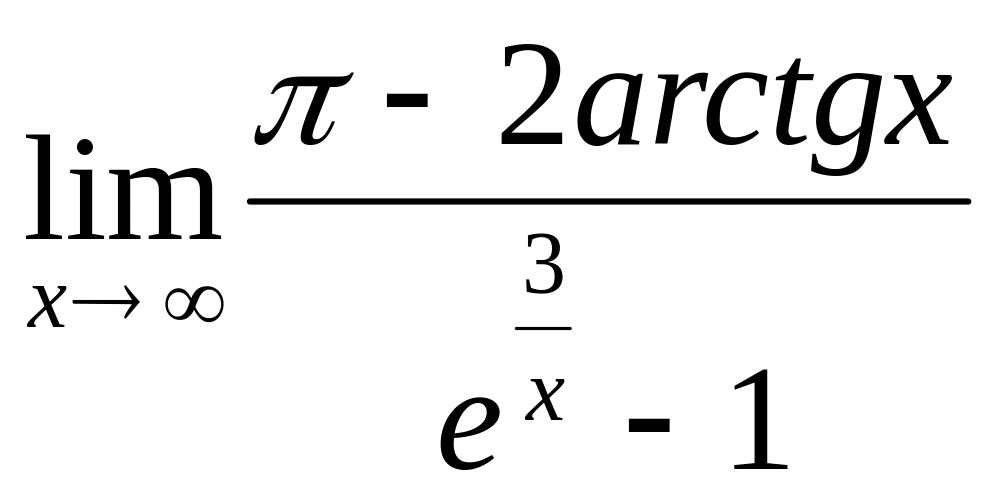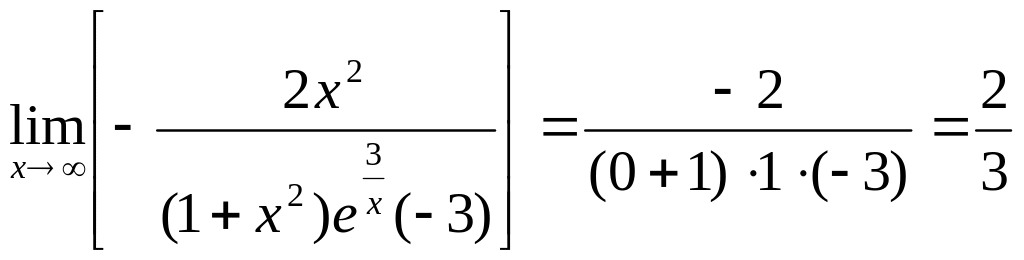Замечание. Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.

Пример. Найти предел . Находим:

; ;

; ;

;

; ;

Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).

Пример. Найти предел . Находим:

; ;

- опять получилась неопределенность. Применим правило Лопиталя еще раз.

; ;

- применяем правило Лопиталя еще раз.

; ;

.

Неопределенности вида можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида , в некоторой окрестноститочки при . Для нахождения предела такой функции достаточно найти предел функции .

Пример. Найти предел .

Здесь , .

Тогда .

Следовательно

Пример. Найти предел . Имеем:

; - получили неопределенность.

Применяем правило Лопиталя еще раз.

; .

17. Производные и дифференциалы высших порядков

Пусть функция дифференцируема на некотором интервале. Дифференцируя, находим её первую производную:

.

Если найти производную функции , получим вторую производную функции если последняя существует:

,

т.е. или .

Этот процесс можно продолжить и далее, находя производные степени .

.

18. Правила нахождения производных высших порядков

Если функции и дифференцируемы, то

1. ;

2. ;

3)

.

Это выражение называется формулой Лейбница.

Также по формуле может быть найден дифференциал - го порядка.

4.5 Исследование функции с использованием производной

1. Исследование функции на возрастание и убывание

Теорема. 1) Если функция имеет производную на отрезке и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. .

2) Если функция непрерывна на отрезке и дифференцируема на промежутке , причем для , то эта функция возрастает на отрезке .

Доказательство. 1) Если функция возрастает, то при и при . Тогда:

2) Пусть для любых точек и , принадлежащих отрезку , причем . Тогда по теореме Лагранжа находим , .

По условию , следовательно, , т.е. функция возрастает.

Теорема доказана.

Аналогично можно доказать, что если функция убывает на отрезке , то на этом отрезке. Если в промежутке , то убывает на отрезке .

Конечно, данное утверждение справедливо, если функция непрерывна на отрезке и дифференцируема на интервале .

Определение. Функция имеет в точке максимум, если ее значение в этой точке больше значений во всех точках некоторой окрестности, содержащей точку . Функция имеет в точке минимум, если при любом ( может быть и отрицательным).

Оределение. Точки максимума и минимума функции называются точками экстремума.

Теорема. (необходимое условие существования экстремума) Если функция дифференцируема в точке и точка является точкой экстремума функции, то производная функции обращается в нуль в этой точке.

Доказательство. Предположим, что функция имеет в точке максимум (для минимума доказательство аналогично). Тогда при достаточно малых положительных верно неравенство:

, т.е. .

Тогда

.

По определению:

,

т.е. если , но , то , а если , но , то .

А это возможно только в том случае, если при Теорема доказана.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то отсюда вообще говоря не следует, что в этой точке функция имеет экстремум. Например, функция имеет производную в точке равную нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.

Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но не достаточные. Например, и .

Вообще говоря, функция может иметь экстремум в точках, где производная не существует или равна нулю.

Теорема. (Достаточные условия существования экстремума) Пусть функция определена и непрерывна в интервале , содержащим критическую точку , и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки ).

Если при переходе через точку слева направо производная функции меняет знак с “+” на “-“, то в точке функция имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет в точке минимум.

Доказательство. Пусть 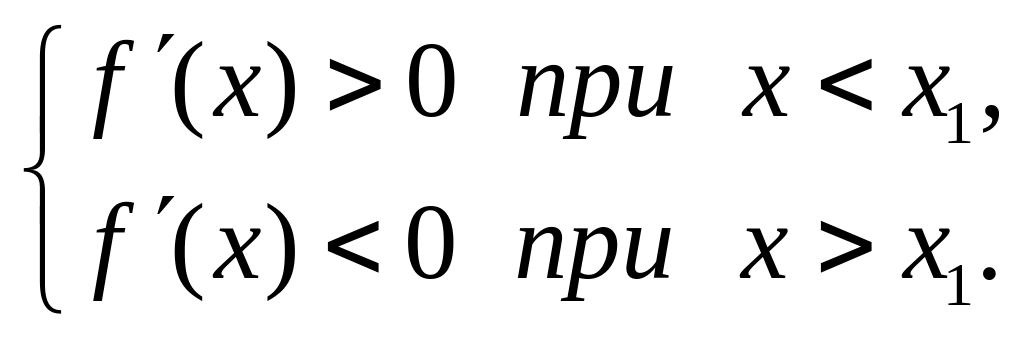По теореме Лагранжа: , где .

Тогда: 1) Если , то ; ; . Следовательно

или .

2) Если , то ; ; . Следовательно

или .

Так как ответы совпадают, то в любых точках в некоторой окрестности точки , т.е. – точка максимума. Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.

На основе вышесказанного можно сформулировать алгоритм для нахождении наибольшего и наименьшего значения функции на отрезке:

1. Найти критические точки функции.

2. Найти значения функции в критических точках.

3. Найти значения функции на концах отрезка.

4. Выбрать среди полученных значений наибольшее и наименьшее.