1 .2. Определители. Решение систем линейных уравнений методом Крамера

Любая квадратная матрица обладает числовой характеристикой, которая называется определителем этой матрицы.

Определителем второго порядка матрицы А размерности 2×2 называется число

(1.2.1)

Пример 1.2.1. Дана матрица . Найти определитель матрицы А.

Решение: Δ

О пределителем третьего порядка матрицы А размерности 3×3 называется число

Пример 1.2.2. Дана матрица . Найти определитель матрицы А.

Решение:

Определитель четвертого порядка вычисляется через определители третьего порядка по аналогичной формуле. Формула носит название разложения Лапласа и позволяет раскладывать определители любого порядка по элементам любой строки или столбца.

Рассмотрим систему n линейных уравнений c n переменными общего вида

(1.2.3)

Решение данной системы находится по формулам Крамера (если ), где - главный определитель системы

, (1.2.4)

а определители получаются из определителя путем замены столбца с номером i на матрицу-столбец свободных членов.

Пример 1.2.3. Решить систему линейных уравнений методом Крамера

Р ешение: вычислим определители системы и найдем решение по формулам Крамера

Т огда

Ответ: (-1, 3, 2) Δ

З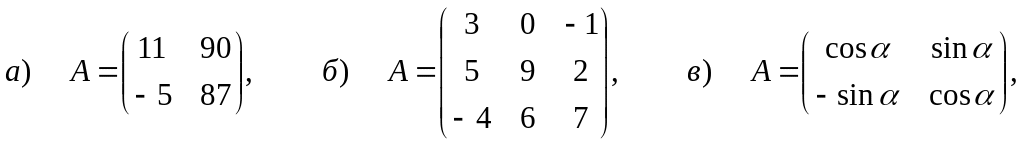 адача 1. Вычислить определители следующих матриц:

Задача 2. Решить системы линейных уравнений методом Крамера:

1.3. Решение систем линейных уравнений методом Гаусса

Рассмотрим систему n линейных уравнений c n переменными общего вида

( 1.3.1)

Расширенной матрицей системы называется матрица всех ее коэффициентов вида

(1.3.2)

Две расширенные матрицы называются эквивалентными, если соответствующие им системы линейных уравнений эквивалентны (имеют одинаковое решение). Например, расширенные матрицы

и являются эквивалентными,

так как соответствующие им системы линейных уравнений

и

имеют решение

Метод Гаусса для решения системы линейных уравнений основан на элементарных преобразованиях расширенной матрицы. В результате каждого из элементарных преобразований расширенная матрица изменяется, однако система линейных уравнений, соответствующая полученной матрице, эквивалентна исходной системе линейных уравнений. Следующие преобразования расширенных матриц называются преобразованиями Жордана-Гаусса и не нарушают их эквивалентность:

1. Любые две строки матрицы можно поменять местами.

2. Любую строчку матрицы можно умножить или разделить на любое, не равное нулю, действительное число.

3. К любой строке матрицы можно прибавить любую другую строчку, умноженную на произвольное число.

4. Любые два столбца расширенной матрицы до разделительной черты можно поменять местами с запоминанием первоначального положения (т.е. той переменной, коэффициентами которой он является).

Алгоритм метода Гаусса:

1. Составить расширенную матрицу системы линейных уравнений.

2. Преобразовать расширенную матрицу к трапециевидной форме с помощью эквивалентных преобразований.

3. Составить систему линейных уравнений, соответствующую последней расширенной матрице, и решить ее, начиная с самого короткого уравнения.

Пример 1.3.1. Решить систему линейных уравнений методом Гаусса

Решение:

1. Составим расширенную матрицу данной системы линейных уравнений:

2. Преобразуем полученную матрицу к трапециевидной форме:

Составим систему линейных уравнений, соответствующую послед

1. ней расширенной матрице и решим ее

Ответ: (1, 5, 2) Δ

Метод Гаусса используется также при решении систем линейных уравнений, в которых количество уравнений не совпадает с количеством переменных.

Примечание: если в процессе элементарных преобразований расширенной матрицы получена строка вида

,

то ее следует удалить из расширенной матрицы и продолжать преобразования далее, если получена строка вида

, где - ненулевое число,

то решение задачи завершено, а система линейных уравнений несовместна, т.к. соответствующее уравнение

не имеет решений.

Система линейных уравнений называется

- совместной, если она имеет хотя бы одно решение;

- несовместной, если не имеет решений;

- определенной, если имеет ровно одно решение;

- неопределенной, если имеет множество решений. Решение в этом случае называется общим.

Задача 1. Решить систему линейных уравнений методом Гаусса:

З адача 2. Решить систему методом Гаусса: