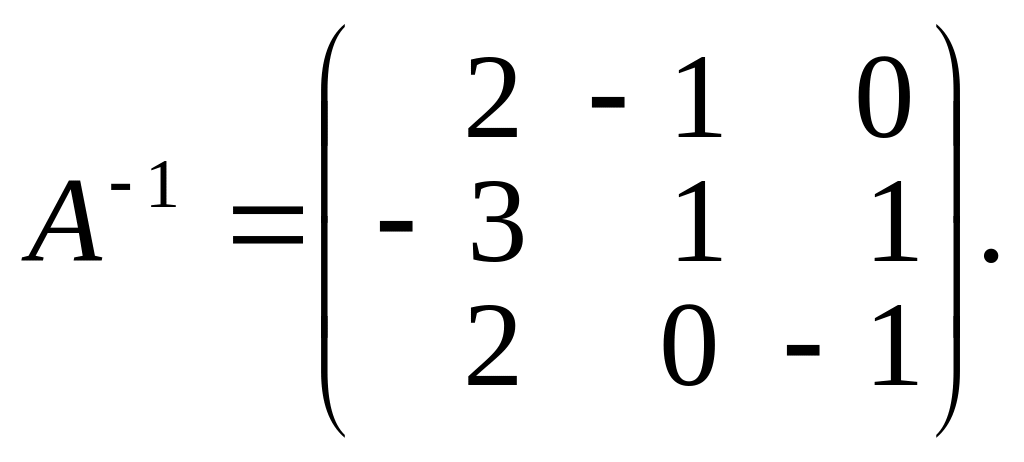- •Глазов 2005
- •Введение
- •Занятие 1 Тема: «Матрицы и действия над ними»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •Решение.
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 2 Тема: «Определители и их свойства»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •Решение. По определению определителя второго порядка
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 3 Тема: «Ранг матрицы»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 4 Тема: «Системы линейных уравнений»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 5 Тема: «Векторы. Линейные операции над векторами»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 6 Тема: «Базис. Координаты вектора в данном базисе»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 7 Тема: «Скалярное произведение векторов»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 8 Тема: «Аффинная и прямоугольная декартовы системы координат»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 9 Тема: «Векторное и смешанное произведения векторов»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 10 Тема: «Различные уравнения прямой на плоскости. Взаимное расположение двух прямых на плоскости»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 11 Тема: «Расстояние от точки до прямой. Направленный угол между двумя прямыми»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 12 Тема: «Плоскость в пространстве»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 13 Тема: «Прямая в пространстве»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 14 Тема: «Взаимное расположение прямой и плоскости»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 15 Тема: «Эллипс. Гипербола. Парабола»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •I II. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Занятие 16 Тема: «Изучение поверхностей второго порядка по их каноническим уравнениям»
- •I. Контрольные вопросы и задания
- •II. Типовые задачи с решениями
- •Решение. Приведем уравнение поверхности ф к каноническому виду, разделив обе части на 36: Это уравнение определяет конус с вершиной в начале координат.
- •III. Задачи для упражнений
- •IV. Задачи для самостоятельного решения
- •V. Задание на дом
- •Список рекомендуемой литературы Список основной литературы
- •Список дополнительной литературы
Занятие 2 Тема: «Определители и их свойства»
Литература для самостоятельного изучения темы: [1], гл. VII; [2], разд. I, гл. 2; [3], гл. 3; [4], гл. 3; [5], гл. V; [6], гл. VI; [7], гл. 1; [8], гл. 1; [9], гл. 10; [10], гл. 7.
I. Контрольные вопросы и задания
1. Дайте определение
определителя второго порядка,
соответствующего матрице
![]()
2. Перечислите
элементы определителя
![]() ,
образующие:
,
образующие:
а) главную диагональ; б) побочную диагональ.
3. Что произойдет с величиной определителя, если:
а) заменить его строки соответствующими столбцами;
б) к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на одно и то же число;
в) поменять местами две строки или два столбца;
г) элементы какой-либо строки или столбца увеличить в k раз, где k – действительное число?
4. Что вы можете сказать о величине определителя, если:
а) элементы какой-либо его строки или столбца равны 0;
б) элементы двух его строк или двух столбцов соответственно равны или пропорциональны?
5. Дайте определение определителя третьего порядка, соответствующего матрице
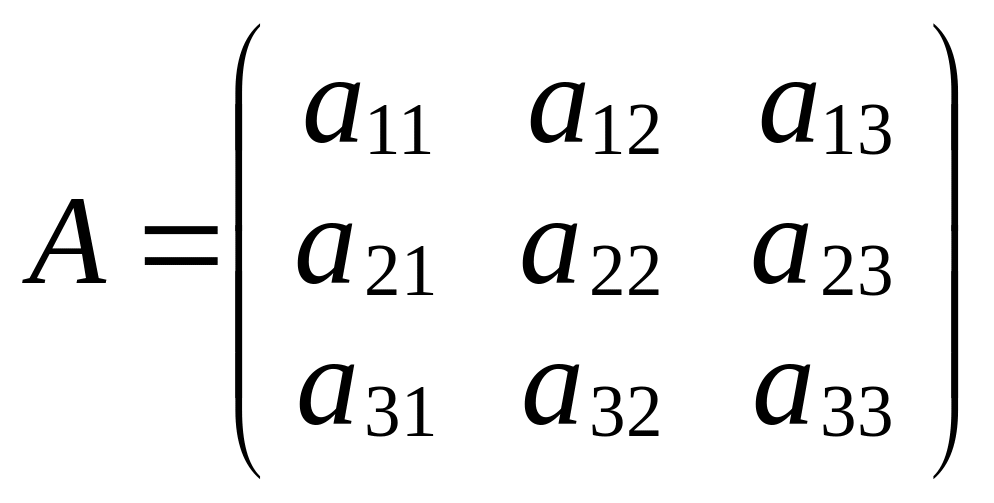 .
.
6. Чему равен определитель произведения двух квадратных матриц?
7. Дайте определение минора какого-либо элемента определителя.
8. Дайте определение алгебраического дополнения элемента аij данного определителя.
9. Чему равен определитель n-го порядка?
10. Дайте определения вырожденной и невырожденной матриц.
11. Как можно найти матрицу, обратную данной, с помощью алгебраических дополнений элементов данной матрицы?
12. Как можно найти матрицу, обратную данной, с помощью элементарных преобразований (метод Жордана)?
II. Типовые задачи с решениями
Задача 1.
Вычислите определитель
![]() .
.
Решение. По определению определителя второго порядка
Ответ:
![]()
Задача 2.
Вычислите определитель третьего порядка
 тремя способами:
тремя способами:
1) с помощью определения;
2) с помощью разложения по элементам какой-либо строки (столбца);
3) преобразованием его с помощью свойств.
Решение.
1)

![]()
2) Разложим определитель третьего порядка по элементам первой строки:
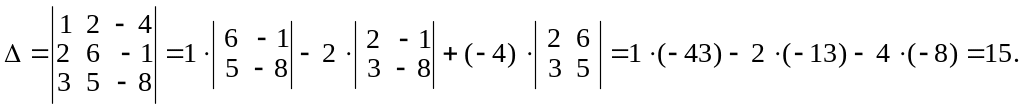
3) Умножая первую
строку на
![]() и прибавляя ко второй, затем умножая
первую строку на
и прибавляя ко второй, затем умножая
первую строку на
![]() и прибавляя к третьей, получаем:
и прибавляя к третьей, получаем:

Далее переставим местами вторую и третью строки:
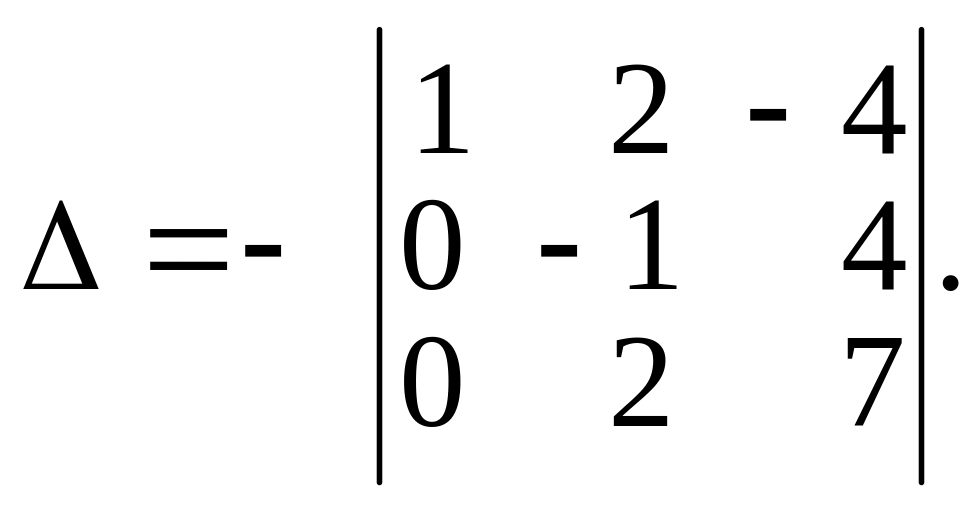
И, наконец, умножая вторую строку на 2 и прибавляя к третьей, получим:

Ответ:
![]()
Замечание.
Определитель
![]() в задаче 2 можно было вычислить и так:
сначала привести его к виду
в задаче 2 можно было вычислить и так:
сначала привести его к виду
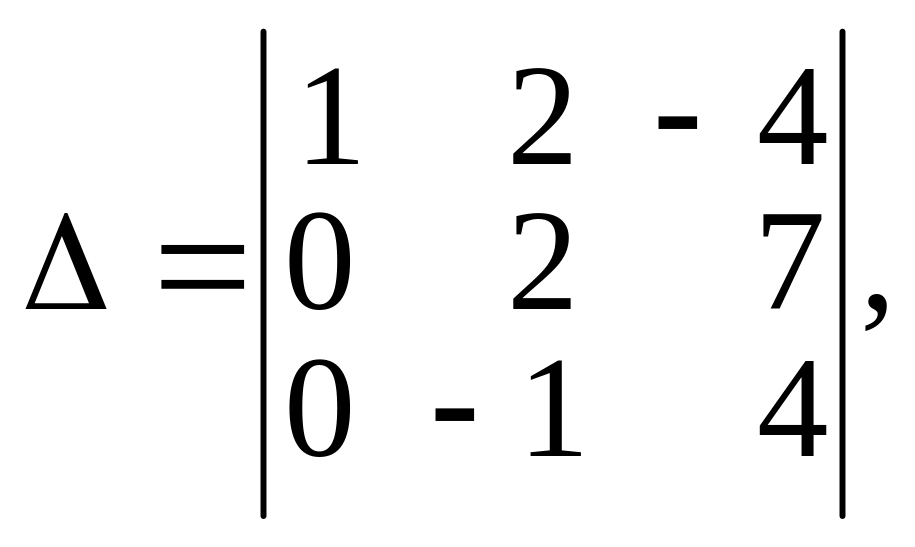 а затем разложить по элементам первого
столбца.
а затем разложить по элементам первого
столбца.
Задача 3.
Вычислите определитель матрицы

Решение. Разложим данный определитель четвертого порядка по элементам первой строки:
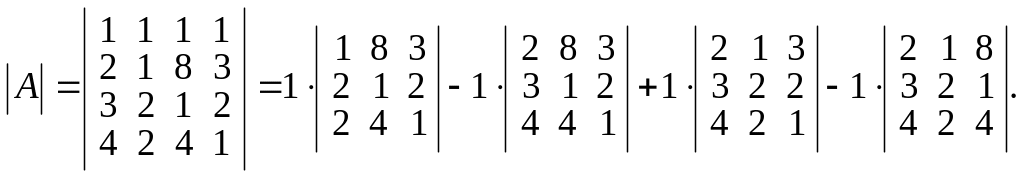
Вычисляя определители
третьего порядка, находим:
![]()
Этот определитель можно вычислить путем его преобразований на основании свойств:

Ответ:
![]()
Задача 4.
Найдите матрицу, обратную матрице:

Решение. Вычислим определитель данной матрицы:

Так как
![]() ,
то матрица А
имеет обратную
матрицу. Найдем алгебраические дополнения
элементов матрицы А:
,
то матрица А
имеет обратную
матрицу. Найдем алгебраические дополнения
элементов матрицы А:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Тогда
.
Тогда

Ответ:
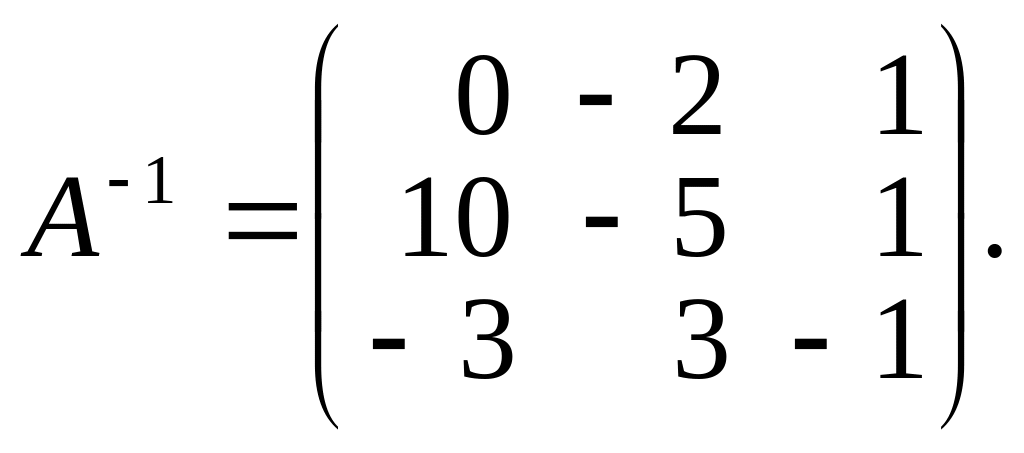
Задача 5.
С помощью элементарных преобразований
найти матрицу
![]() ,
обратную матрице
,
обратную матрице
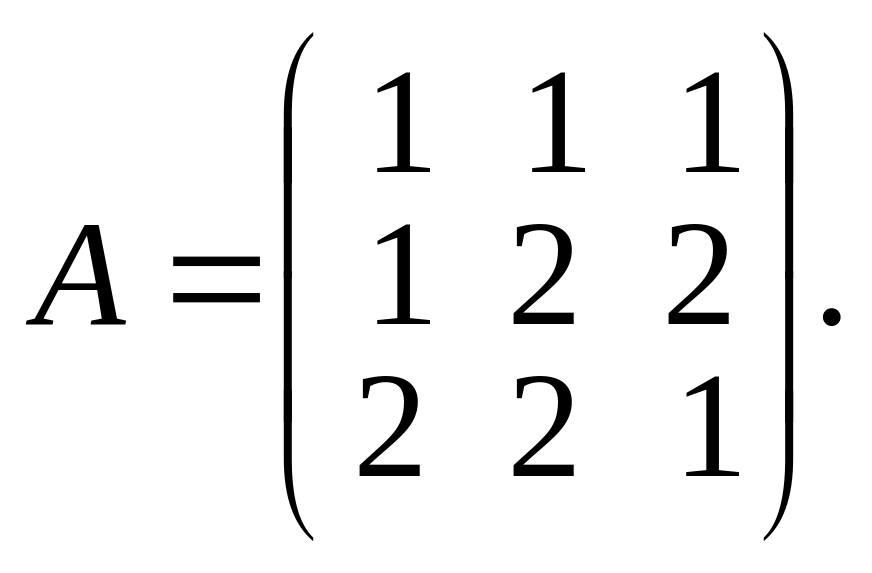
Решение.
Составляем матрицу
![]() и преобразуем ее, приводя матрицу А
к единичной. При этом матрица Е
будет приведена к
:
и преобразуем ее, приводя матрицу А
к единичной. При этом матрица Е
будет приведена к
:



Вторая матрица получена из первой в результате следующих элементарных преобразований: элементы первой строки умножены на (–1) и сложены с элементами второй строки, элементы первой строки умножены на (–2) и сложены с элементами третьей строки.
Умножив последнюю строку второй матрицы на (–1), получим третью матрицу.
Умножая третью строку на (–1) и прибавляя ко второй, а затем к первой строке, получаем четвертую матрицу. Умножая ее вторую строку на (–1) и прибавляя к первой строке, получаем пятую матрицу: слева от черты – единичная матрица, справа – матрица А–1, обратная исходной матрице А.
Ответ: