II. Типовые задачи с решениями

Задача 1. Найдите проекцию точки на плоскость

Решение. Этой проекцией является точка пересечения перпендикуляра к плоскости, проходящего через точку М. Для прямой, перпендикулярной плоскости, направляющим вектором будет (рис. 28).

П араметрические уравнения прямой, перпендикулярной плоскости и проходящей через точку М, примут вид:

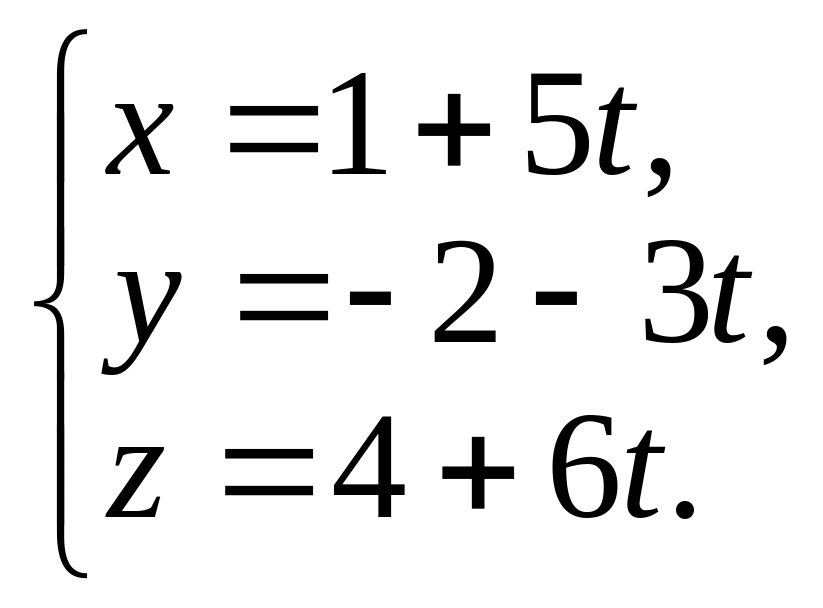
Подставляя эти значения в уравнение плоскости, находим:

При этом значении t из параметрических уравнений прямой получаем: Следовательно, точка – искомая проекция.

Ответ:

Задача 2. Докажите, что прямая лежит в плоскости

Решение. Найдем координаты направляющего вектора данной прямой: отсюда

Вектор нормали плоскости равен

значит, прямая либо параллельна плоскости, либо лежит в плоскости.

Найдем какую-либо точку прямой и проверим, лежит ли она в плоскости. Положив, например, из системы получаем Таким образом, точка прямой найдена. Подставляя ее координаты в уравнение плоскости, получаем верное равенство:

Следовательно, данная прямая лежит в данной плоскости.

З адача 3. Составьте уравнение плоскости , проходящей через точку перпендикулярно к прямой

Решение. Так как то (рис. 29).

Следовательно, плоскость задана точкой и вектором нормали Поэтому уравнение имеет вид: откуда

Ответ:

III. Задачи для упражнений

1. Докажите, что прямая параллельна плоскости

2. Найдите точку пересечения прямой и плоскости

3. Составьте уравнение прямой, проходящей через точку перпендикулярно к плоскости

4. Составьте уравнение плоскости, проходящей через точку перпендикулярно к прямой

5. При каком значении С прямая параллельна плоскости

6. При каких значениях l и C прямая перпендикулярна к плоскости

IV. Задачи для самостоятельного решения

1. Составьте уравнение плоскости, проходящей через прямую перпендикулярно к плоскости

2. Напишите уравнение плоскости, проходящей через параллельные прямые и

3. Напишите уравнение перпендикуляра, опущенного из начала координат на прямую

4. Составьте уравнение плоскости, проходящей через точку параллельно прямым

5. Составьте канонические уравнения прямой, которая проходит через точку параллельно плоскости и пересекает прямую

6. Найдите точку Q, симметричную точке относительно прямой

7. Найдите угол между прямой 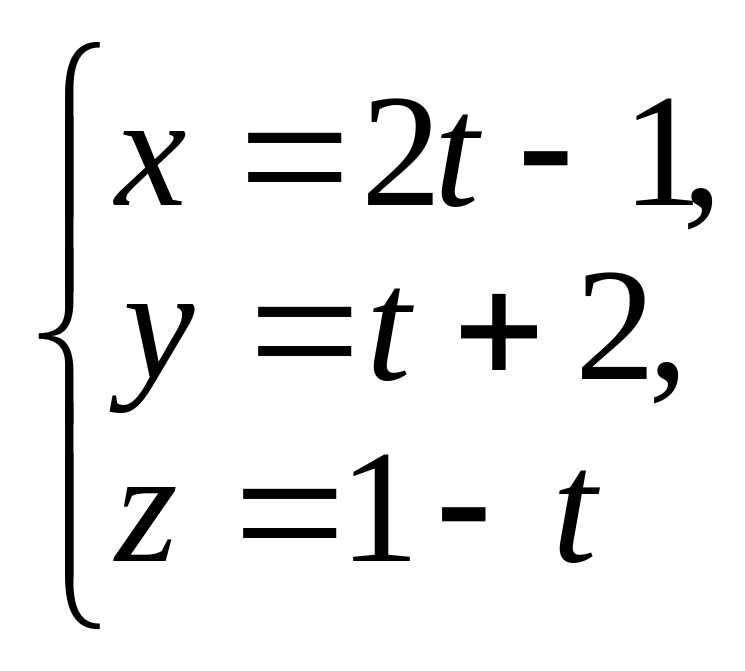и плоскостью

V. Задание на дом

1. Докажите, что прямая параллельна плоскости а прямая лежит в этой плоскости.

2. Напишите уравнение плоскости, проходящей через прямую и точку

3. Напишите уравнение плоскости, проходящей через прямую и перпендикулярной плоскости

4. Найдите угол между прямой и плоскостью

5. При каких значениях А и В плоскость перпендикулярна к прямой

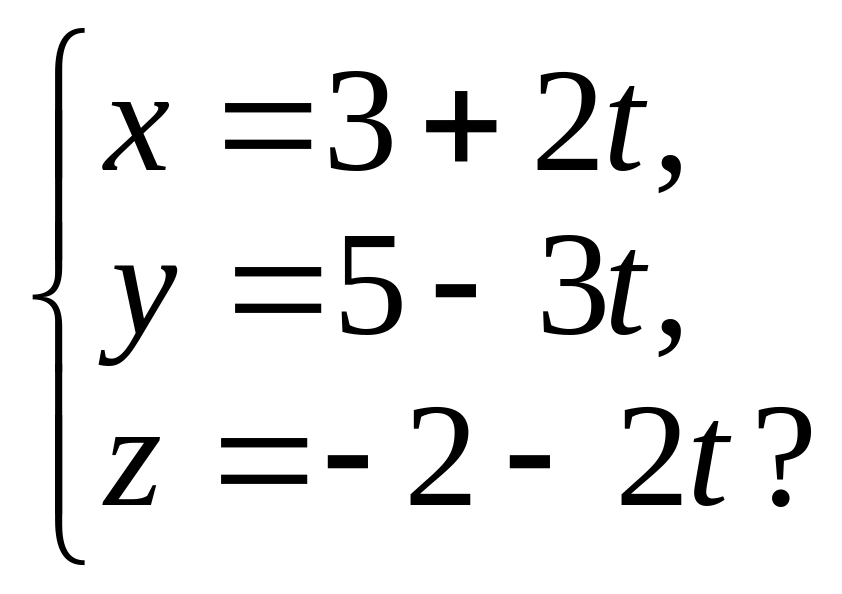
Занятие 15 Тема: «Эллипс. Гипербола. Парабола»

Литература для самостоятельного изучения темы: [1], гл. VI; [2], разд. I, гл. 1; [3], гл. 5; [4], гл. 5; [5], гл. III; [6], гл. III; [7], гл. 6; [8], гл. 6; [9], гл. 3; [10], гл. 3.