II. Типовые задачи с решениями

Задача 1. Найдите канонические уравнения прямой

Решение. Полагая, например, из системы получаем Таким образом, точка прямой найдена.

Теперь определим направляющий вектор данной прямой: т.е.

Запишем канонические уравнения прямой:

Ответ:

Задача 2. Докажите, что прямые и пересекаются. Найдите точку их пересечения

Решение. Прямая задана фиксированной точкой и направляющим вектором . Прямая задана фиксированной точкой и направляющим вектором .

Докажем, что прямые и лежат в одной плоскости, т.е. что смешанное произведение векторов и равно нулю, и что векторы и не коллинеарны.

, т.к. значит, прямые и пересекаются.

Составим из их канонических уравнений систему:

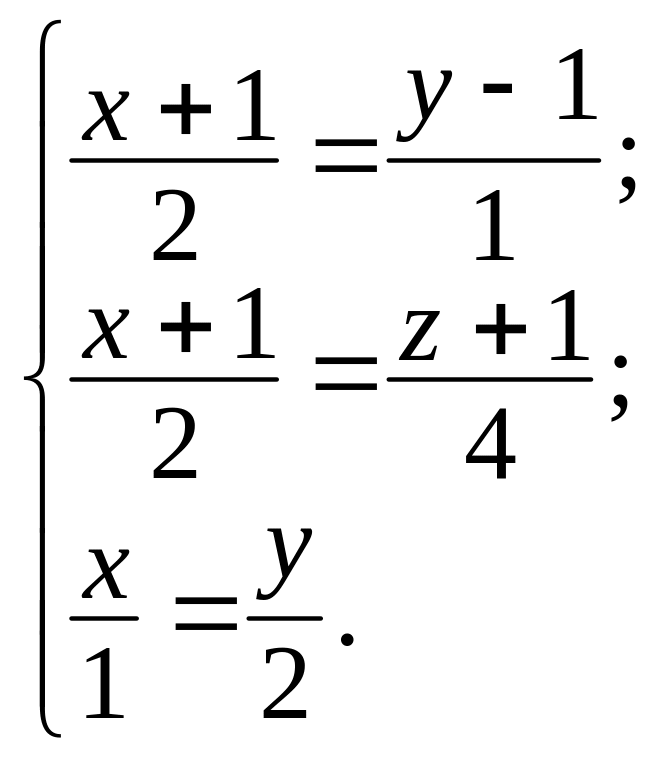
Решив ее, находим координаты точки пересечения данных прямых:

x = 1, y = 2, z = 3.

Ответ: (1;2;3).

III. Задачи для упражнений

1 . Составьте уравнение прямой:

а) проходящей через две точки ;

б) проходящей через точку параллельно вектору ;

в) образованной пересечением плоскости с координатной плоскостью Oxy.

2. Напишите параметрические уравнения следующих прямых:

а) б)

3. Через точку М(1;–3;4) проведите прямую, параллельную прямой

4. Найдите тупой угол между прямым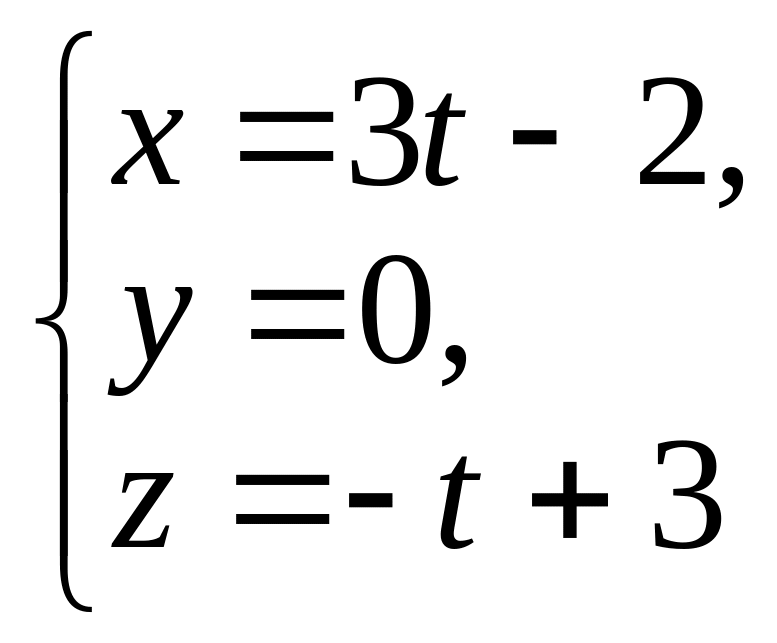и: и

5. Установите взаимное расположение следующих пар прямых:

а) 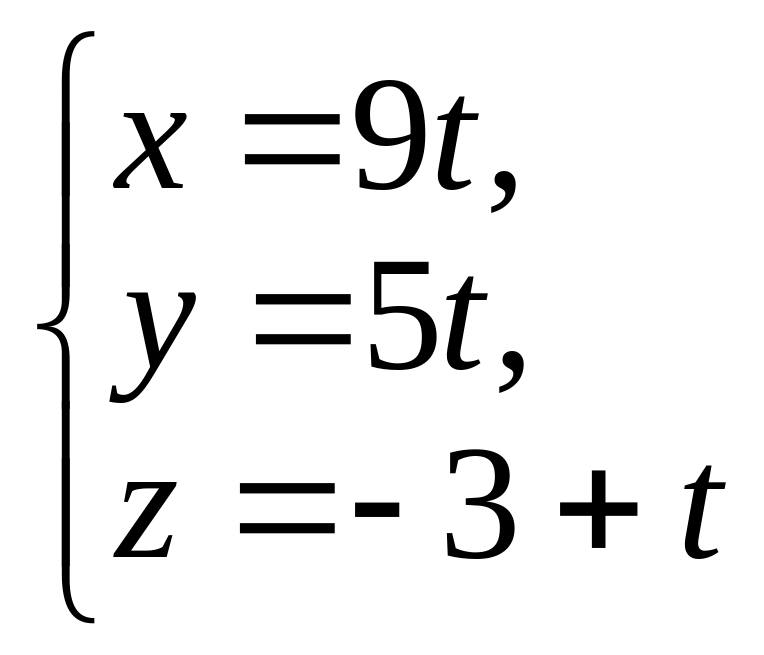и

б) и

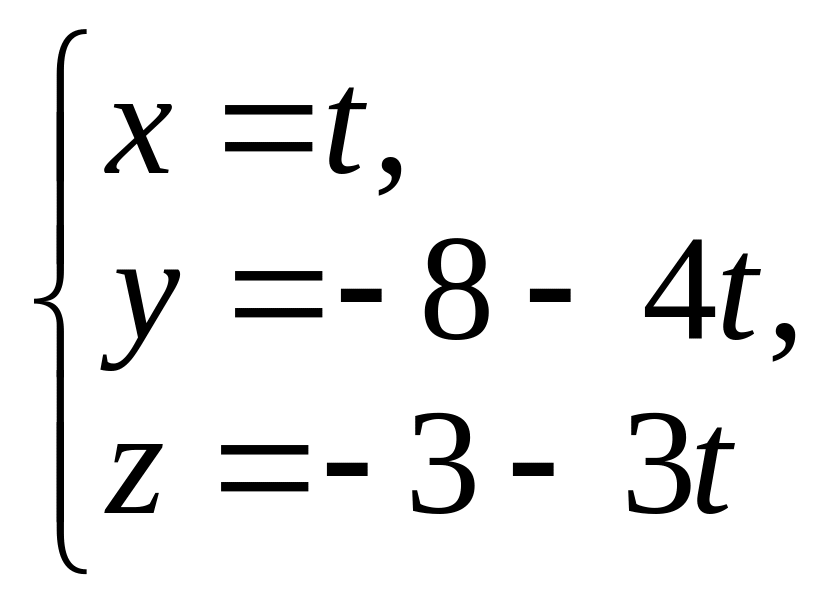в) и

6. Составьте уравнение плоскости, проходящей через прямую и параллельной прямой

IV. Задачи для самостоятельного решения

1. Составьте уравнение прямой, которая проходит через точку и пересекает прямые

2. Через точку А(1;0;–1) проведите прямую, перпендикулярную к прямой и пересекающую прямую

3. При каком D прямая пересекает ось Oy?

4. Найдите расстояние точки М(2;–1;3) от прямой

V. Задание на дом

1. Найдите острый угол между прямыми:

2. Докажите перпендикулярность прямых: и

3. Докажите параллельность прямых: и

4. Установите взаимное расположение прямых и

5. Определите координаты точки, лежащей на прямой и имеющей ординату, равную –1.

Занятие 14 Тема: «Взаимное расположение прямой и плоскости»

Литература для самостоятельного изучения темы: [2], разд. I, гл. 3; [3], гл. 4; [4], гл. 4; [5], гл. II; [6], гл. II; [7], гл. 5; [8], гл. 5; [9], гл. 9; [10], гл. 10.

I. Контрольные вопросы и задания

1. Какой угол называется углом между прямой и плоскостью?

2. Напишите формулу нахождения синуса угла между прямой и плоскостью.

3. Найдите угол между прямой и плоскостью , если

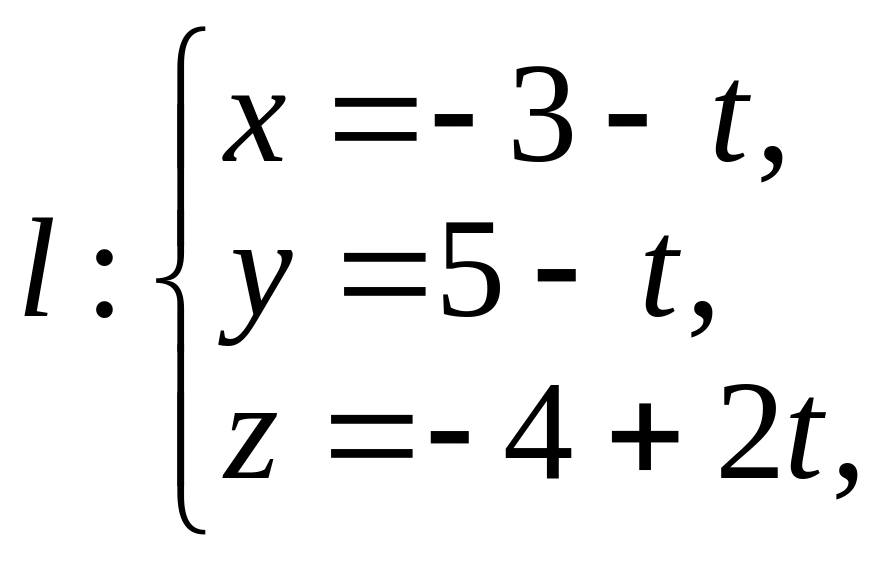
4. Напишите условие пересечения прямой и плоскости.

5. Как найти точку пересечения прямой с плоскостью

6. Сформулируйте необходимый и достаточный признак параллельности прямой и плоскости.

7. Сформулируйте необходимый и достаточный признак перпендикулярности прямой и плоскости.

8. Напишите условие принадлежности прямой плоскости.