II. Типовые задачи с решениями

Задача 1. Вершины треугольника находятся в точках Вычислите его площадь и длину высоты, проведенной из вершины В.

Р ешение. Воспользуемся формулой

Найдем координаты векторов и :

Сначала найдем координаты вектора

т.е.

Затем найдем длину вектора :

Тогда (кв. ед.).

Чтобы найти высоту ВН (рис. 22), воспользуемся формулой

тогда (ед.).

Ответ: кв. ед., ед.

Задача 2. Найдите объем и длину высоты параллелепипеда ABCDA₁B₁C₁D₁ (рис. 23), если

Решение. ;

Т огда (куб. ед.).

Для нахождения высоты А₁Н (рис. 23) воспользуемся формулой: откуда ;

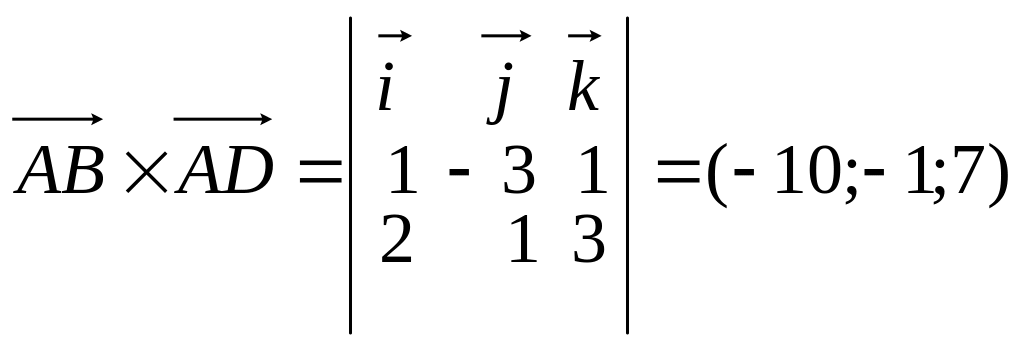Ответ: куб. ед.,

Задача 3. Докажите, что векторы компланарны.

Решение. Векторы компланарны тогда и только тогда, когда их смешанное произведение равно 0.

следовательно, векторы компланарны.

Задача 4. При каком значении x вектор перпендикулярен вектору если

Решение. Первый способ. Найдем сначала координаты вектора Вектор перпендикулярен вектору тогда и только тогда, когда Найдем скалярное произведение Следовательно, получаем уравнение откуда находим

Второй способ. Не находя координат вектора запишем условие перпендикулярности векторов и Но в левой части этого равенства стоит смешанное произведение трех векторов следовательно, Подставляя в это равенство координаты векторов получим уравнение:

откуда т.е.

Ответ:

III. Задачи для упражнений

1. Вычислите синус угла, образованного векторами и

2. Вычислите площадь треугольника, вершины которого находятся в точках

3. Найдите длину высоты ВН параллелограмма ABCD, проведенной к основанию AD, если

4. Вычислите объем треугольной пирамиды, вершины которой находятся в точках

5. Даны вершины тетраэдра Найдите длину его высоты, опущенной из вершины D.

6. Будут ли компланарны векторы:

а) ; б) ?

7. Выясните, лежат ли точки и в одной плоскости.

8. При каком значении y вектор перпендикулярен вектору если

IV. Задачи для самостоятельного решения

1. Площадь треугольника АВС равна кв. ед. Две его вершины находятся в точках и Найдите координаты третьей вершины С, если она лежит на оси Oz.

2. Вектор перпендикулярен к векторам угол между равен 30⁰. Зная, что вычислите

3. Дан параллелепипед ABCDA₁B₁C₁D₁, построенный на векторах и Найдите: а) косинус угла между гранями и

б) объем параллелепипеда;

в) площади граней;

г) длину высоты, проведенной из вершины А₁ на грань

4. Объем тетраэдра V = 5, три его вершины находятся в точках Найдите координаты четвертой вершины D, если известно, что она лежит на оси Oy.

V. Задание на дом

1. Даны точки Вычислите площадь треугольника АВС.

2. Даны вершины треугольника и Вычислите длину его высоты, опущенной из вершины В на сторону АС.

3. В треугольной призме и Вычислите: а) объем призмы;

б) площади граней;

в) длину высоты призмы.

4. Объем треугольной пирамиды равен 9. Три его вершины находятся в точках Найдите координаты четвертой вершины D, если она находится на оси Oz.