
- •Глава 1
- •§ 1. Основные понятия
- •0,1010010001 ... 1000 ... 01 ... Иррационально.
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3.Бесконечно большие и бесконечно малые последовательности.
- •§2.Сходящиеся последовательности
- •1.Определение предела последовательности.
- •2.Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Глава 3. § 4- § 8.
- •Глава 4
- •§ 1.Основные понятия
- •Глава 4§1. Пример5.- Пример9.
- •Глава 4§2.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
§ 3. Абсолютная величина вещественного числа
Определение.
Абсолютной
величиной (или модулем) числа x
называется само число x,
если
 ,
или число - x,
если
,
или число - x,
если
 .
.
Абсолютная
величина числа x
обозначается символом
 .
Таким
образом,
.
Таким
образом,

Например,
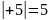 ;
; ;
; .
.
Основные
свойства абсолютных величин:
1º.
 .
2º.
.
2º.
 .
3º.
.
3º.
 .
4º.
Неравенство
.
4º.
Неравенство
 означает, что
означает, что
 .
5º.
Неравенство
.
5º.
Неравенство
 означает, что либо
означает, что либо
 ,
либо
,
либо
 .
6º.
.
6º. .
7º.
.
7º.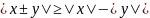 .
8º.
.
8º. .
9º.
.
9º. .
.
Пример
1. Найти решения
уравнений: 1)
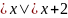 ;
2)
;
2)
 ;
3) x+2|x|=3.
;
3) x+2|x|=3.
Решение.
1) При
имеем
 ,
откуда
,
откуда
 - неверное равенство; следовательно
решений нет. При
получаем
- неверное равенство; следовательно
решений нет. При
получаем
 ,
откуда
,
откуда
 - решение уравнения.
- решение уравнения.
2)
При
имеем
 ,
откуда
,
откуда
 - неверное равенство; следовательно
решений нет. При
получаем
- неверное равенство; следовательно
решений нет. При
получаем
 ,
откуда
,
откуда
 ,
что противоречит сделанному предположению
.
Таким образом, уравнение не имеет
решений.
,
что противоречит сделанному предположению
.
Таким образом, уравнение не имеет
решений.
3)
При
имеем
 ,
откуда
,
откуда
 .
При
получаем
.
При
получаем
 ,
откуда
,
откуда
 .
Следовательно,
и
- решения уравнения.
.
Следовательно,
и
- решения уравнения.
Пример
2. Решить
уравнение
 .
.
Решение.
По определению,
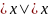 при
.
Следовательно, данное уравнение
представится в виде
при
.
Следовательно, данное уравнение
представится в виде
 ,
откуда
,
откуда
 .
.
Пример
3. Решить
неравенство
 .
.
Решение.
Так как
только при
,
то неравенство справедливо для тех x,
при которых
 ,
откуда
,
откуда
 .
.
Пример
4. Решить
неравенство .
.
Решение.
В силу свойства
5º будем иметь
 или
или
 откуда получаем ответ: либо
,
либо
откуда получаем ответ: либо
,
либо
 .
.
Пример
5. Доказать
неравенство
 .
.
Решение. В силу свойств 2º и 7º имеем
 .
(1)
.
(1)
Умножая
второе неравенство на
 ,
получаем
,
получаем
 . (2)
. (2)
Объединяя
(1) и (2), найдем
 ,
откуда в силу свойства 4º
.
,
откуда в силу свойства 4º
.
Решить уравнения и неравенства:
23. |
|
24. |
. |
25. |
|
26. |
|
27. |
|
28. |
. |
29. |
|
30. |
|
31. |
|
32. |
|
33. |
|
34. |
|
35. |
|
36. |
|
37. |
|
38. |
|
39. |
|
40. |
|
41. |
|
42. |
|
43. |
|
44. |
|
45. |
|
46. |
|
47. |
|
48. |
|
49. |
|
50. |
|
51. |
|
52. |
|
Глава 2
Числовые последовательности и теория пределов
§1. Числовые последовательности
1. Определение числовой последовательности.
Определение 1. Если
каждому числу n
из натурального ряда чисел
1,2,3….n,…..поставлено
в соответствие вещественное число
 , то множество вещественных чисел
, то множество вещественных чисел
,
 ,
,
 ……..
……
……..
……
называется числовой последовательностью или просто последовательностью.
Числа , , …….. …….называются элементами (членами) последовательности, символ - общим элементом ( членом) последовательности, а n-номером элемента. Кратко последовательность обозначают { } .
Последовательности
{
+ },
{
-
},
{
},
{
-
},
{
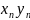 },
{
/
},
≠0
называются соответственно суммой,
разностью, произведением и частным
двух последовательностей: {
}
и {
}
},
{
/
},
≠0
называются соответственно суммой,
разностью, произведением и частным
двух последовательностей: {
}
и {
}
Пример 1. Дана
формула общего элемента последовательности
=
 .Написать пять первых элементов
последовательности .
.Написать пять первых элементов
последовательности .
Решение. Полагая
последовательно n=1,2,3,4,5
в общем элементе
,
получаем
=1/2,
=2/3,
=3/4,
 =4/5,
=4/5,
 =5/6
.
=5/6
.
1.Написать пять
первых элементов каждой из
последовательностей, заданных их общими
элементами: 1)
=
 ; 2)
=
; 2)
=
 ; 3)
=
; 3)
=
 ; 4)
=
; 4)
=

2. Зная несколько первых элементов последовательности, написать формулу общего элемента последовательности:
1) 1;
 ;
;
 ;
;
 ; …….; 2) 1;
; …….; 2) 1;
 ;
;
 ;
;
 ;
…….; 3) 1; 2
;
…….; 3) 1; 2 ; 2
; 2 ; 3
; 3 ;
3
;
3 ; ….;
; ….;
4) 2; 10; 26; 82; 242; 730; 5)-1; 1; -1; 1; -1; …..
3. Написать пять первых элементов и формулу общего элемента каждой из последовательностей, заданных их рекуррентными соотношениями:
1)
=1,
 =
!
2)
=1,
=
+3;
3)
=2,
=
*3; 4)
=1,
=
+
+….
=
!
2)
=1,
=
+3;
3)
=2,
=
*3; 4)
=1,
=
+
+….
4. Последовательность
{
}
задается двумя первыми элементами
=0,
=1
и рекуррентным соотношением x……
для любого n≥1. Найти
 и
и
 .
.
2.Ограниченные и неограниченные последовательности. Определение2. Последовательность { } называется ограниченной сверху (снизу), если существует число М(m) такое, что любой элемент этой последовательности удовлетворяет неравенству ≤M ( ≥m).
Определение 3. Последовательность { } называется ограниченной, если она ограничена и сверху и снизу, т.е существуют числа m и M такие, что любой элемент этой последовательности удовлетворяет неравенствам m≤ ≤ M.
Определение 4.
Последовательность {
}
называется неограниченной, если для
любого положительного числа А существует
элемент
этой последовательности, удовлетворяющий
неравенству
 |>A.
|>A.
Примеры. 1. Последовательность 1,2,3,…..,n,…..ограничена снизу (m=1), но не ограничена сверху.
2. Последовательность -1,-2,-3,….., -n, ….ограничена сверху (М=-1), но не ограничена снизу.
Последовательность
1,
 ,
,
 ,
….,
,
….,
 ,
…. Ограничена, так как 0≤
≤1
(m=0, M=1).
,
…. Ограничена, так как 0≤
≤1
(m=0, M=1).
4. Последовательность
-1,2,-3,4,-5,…..(-1 n,
…..-неограниченная, так как для любого
числа А>0 существует элемент этой
последовательности, удовлетворяющий
неравенству |
|>
A,(т. есть либо
>
A либо
<
-A)
n,
…..-неограниченная, так как для любого
числа А>0 существует элемент этой
последовательности, удовлетворяющий
неравенству |
|>
A,(т. есть либо
>
A либо
<
-A)
5. какие из последовательностей являются ограниченными:
1)- 1,
,
-
,
,
-
 ,
….,
,
….,
,
….,
,
….,
 ,
…..;
,
…..;
2) 2; 4; 6; 8; 10; 12; ….;2n;….;
3) sin1; sin2; sin3; sin4; ….; sin n; ….;
4) -1,2,-3,4,-5,
-6, 7…..(-1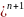 n;
...;
n;
...;
5) ,
,
 ,
,
 ,
,
 ,
….,
,
…..;
,
….,
,
…..;
6) 1;1;1;1;1;1;1;1……;
7)Ln1; Ln2; Ln3; Ln4;……. Ln n; ...?

 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.

 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.