§3. Понятие дифференциала

Если функция дифференцируема в точке x, т.е. имеет в этой точке конечную производную, то ее приращение можно записать в виде:

,

где .

Главная, линейно относительно часть приращения функции называется дифференциалом функции и обозначается :

(1)

Положив в формуле (1) , получим , окончательно соотношение (1) принимает вид

При достаточно малых приращение функции приближенно равно ее дифференциалу, т.е. .

Пример 1. Найти дифференциал функции в точке 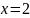, причем сделать это двумя способами: 1) выделяя главную, линейную относительно часть приращения ; 2) по формуле (2).

Решение.

1) , отсюда ;

2) по формуле (2), . Следовательно, получаем .

Пример 2. Вывести приближенную формулу . Найти приближенно ; .

Решение. Возьмем функцию . Тогда при малых или , откуда

Полагая , получим . Найдем приближенно и . Имеем .

Найти дифференциалы функций:

146. ; 147. ;

148. ; 149.

150. ; 151. ;

152. 153. ;

154. ; 155. ;

156. ; 157. ;

158. ; 159. ;

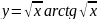160. Найти приближенно приращение функции , если

161. Вывести приближенную формулу . Найти приближенно

§4. Производные и дифференциалы высших порядков

1. Производные высших порядков. Производная называется производной первого порядка. Производная от называется производной второго порядка (или второй производной) от функции и обозначается или 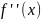. Производная от называется производной третьего порядка (или третьей производной) от функции и обозначается или и т.д.

Производная n-го порядка есть производная от производной -го порядка, т.е. .

Производные, начиная со второй, называются производными высшего порядка.

Найти производные второго порядка от функций:

162. 163. ;

164. ; 165. ;

166. 167. ;

168. 169. ;

170. 171. ;

172. ; 173. .

2. Дифференциалы высших порядков. Дифференциал называется дифференциалом первого порядка.

Дифференциал от дифференциала называется дифференциалом второго порядка функции f(x) и обозначается , т.е. .

Дифференциал от дифференциала называется дифференциалом третьего порядка функции f(x) и обозначается и т.д.

Дифференциал от дифференциала называется дифференциалом n-го порядка функции f(x) и обозначается .

Дифференциал n-го порядка индуктивно определяется по формуле

откуда

т.е. n-я производная функции в некоторой точке равна отношению n-го дифференциала этой функции в точке к дифференциалу аргумента в степени n.

Пример. Найти дифференциал третьего порядка функции .

Решение. Последовательно дифференцируя, получим:

.

Найти дифференциалы второго порядка от функций:

198. ; 199. ;

200. 201. ;

Найти дифференциалы указанных порядков от функций:

202. , найти ; 203. , найти ;

204. 205. , найти ;
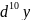