Тема2. Математическое программирование

2.1. Постановка задачи математического программирования. Виды экстремума функций многих переменных

К задачам математического программирования относятся задачи оптимизации, в которых отыскивается экстремум заданной скалярной функции многих переменных при ограничениях в форме системы равенств и неравенств. Все они с формальной точки зрения могут быть сведены к следующей постановке: найти значения переменных ,доставляющие экстремальное значения некоторой функции и удовлетворяющие уравнениям и неравенствам

. (2.1)

Предполагается что функции и известны, а – заданные постоянные величины. Условия (2.1) называются ограничениями. Как правило, отдельно оговариваются ограничения на знак переменных , так как методы их учета могут быть иными, чем сложных ограничений типа (2.1). Могут налагаться условия целочисленности переменных. Кратко условия задачи математического программирования можно записывать следующим образом

.

Если при определении экстремума ограничиться рассмотрением минимизации, задача не теряет общности, так как максимизация функции эквивалентна минимизации функции .

Функция называетсяцелевой функциейилифункциейцели. Переменные , удовлетворяющие совокупности заданных ограничений, представляют собой допустимое решение задачи, и называются планом задачи. Допустимое решение, доставляющие экстремум функции цели , называется оптимальным решением или оптимальным планом. Не каждая задача математического программирования имеет планы, так как не каждая система ограничений имеет решение.

Рассмотрим основные виды экстремума функций конечного числа переменных. Пусть определена в некоторой области переменных . Если на переменные не накладывается никаких ограничений, т.е. область не ограничена, то экстремум функции называется безусловным, а в противном случаеусловным.

Простейшая задача оптимизации связана с нахождением значений переменных, обеспечивающих экстремум функции цели при отсутствии ограничений, т.е. с нахождением безусловного экстремума функции.

Безусловным глобальным минимумом (максимумом)функции называется наименьшее (наибольшее) в пределах всей рассматриваемой областиRзначение этой функции. Если в некоторой точке функция имеет меньшее (большее) значение, чем во всех точках , принадлежащих некоторой малой окрестности точки , то говорят, что в этой точке имеет местолокальный минимум(максимум) функции .

На рис. 2.1, а изображена функция , заданная на неограниченной областиR, здесь в точках и достигается соответственно глобальный безусловный максимум и минимум функции , так как

и для .

В точках и достигается безусловный локальный минимум и максимум функции , так как в окрестностях этих точек удовлетворяются условия

, ,

Очевидно, что если в пределах область Rимеется всего один минимум (максимум), то он является глобальным.

При наличии ограничений область Rограничивается областью допустимых значений переменныхX. В этом случае точки экстремума должны обязательно принадлежать областиXи сам экстремум называется условным. При этом экстремумы называютсяграничными, если они имеют место в граничных точках области ивнутренними, если соответствует внутренним точкам областиX.

На рис. 2.1, б область ограничена значениями . Точке здесь будет соответствовать условный глобальный минимум функции , а точкам и условный локальный и глобальный максимум соответственно. Причём экстремумы в точках и являются граничными. В практических задачах наибольший интерес представляет нахождение глобального условного экстремума.

а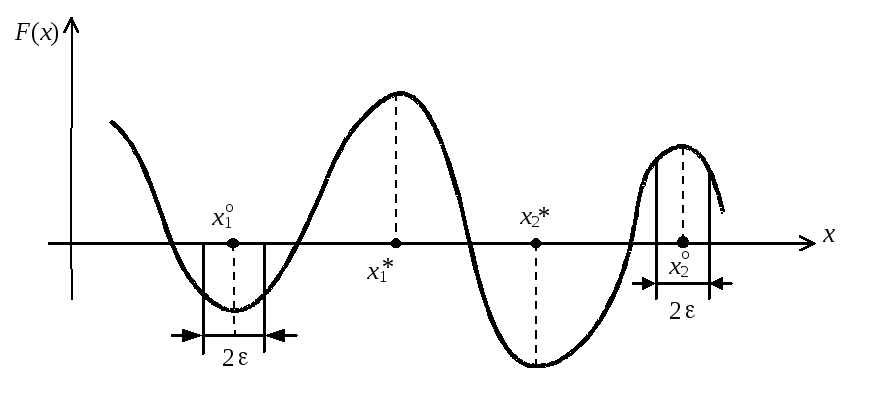

б

.

рис. 2.1. Примеры экстремума функции одной переменной:

а – безусловные; б – условные