4.4.2 Задание плоскости

При работе с полигональными сетками и многоугольниками часто используется уравнение плоскости, в которой лежит многоугольник:

ax + by + cz + d = 0 (4.17)

Три точки, лежащие на плоскости описываются уравнениями:

(4.18)

В том случае, если точки Р, Р1, Р2, Р3 лежат на одной плоскости, должна выполняться система уравнений (4.17 - 4.18). Если эта система уравнений имеет решение, определитель, составленный из ее коэффициентов, должен быть равен 0:

(4.19)

Разлагая этот определитель на алгебраические дополнения по первой строке, получим:

(4.20)

Определители с учетом их знаков являются коэффициентами a,b,c,d уравнения (4.17) соответственно:

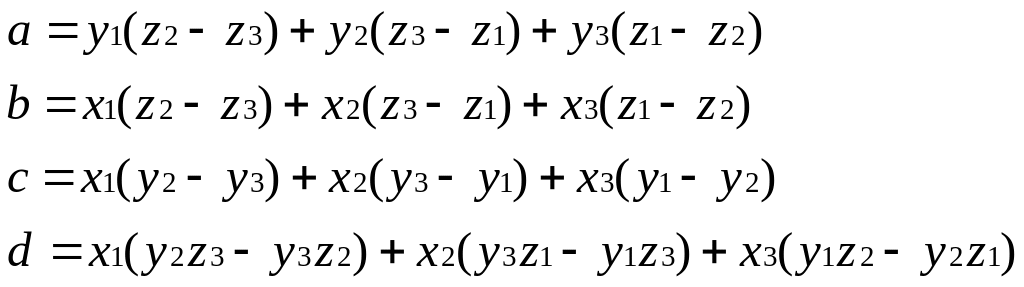(4.21)

Рассмотрим еще один метод вычисления коэффициентов уравнения плоскости. Хотя это уравнение содержит 4 неизвестных коэффициента, его можно нормировать таким образом, чтобы d= 1. Следовательно, трех неколлинеарных точек будет достаточно для определения этих коэффициентов. Подстановка координат трех неколлинеарных точек в систему нормированных уравнений (4.18) дает:

или в матричной форме:

или

X*C= D

Решение этого уравнения дает значение коэффициентов плоскости:

│С│ = │X^-1│ ● │D│ (4.22)

Еще один способ используется в том случае, если известен вектор нормали к плоскости, т.е.:

= ai + bj + ck (4.23)

где i, j, k - единичные векторы осей x, y, z соответственно.

Теперь уравнение плоскости примет вид:

ax + by + cz + d = 0

Величина d вычисляется с помощью произвольной точки на плоскости. Например, если координаты этой точки x1, y1, z1 , то

d = - (ax1 + by1 + cz1) (4.24)

Поскольку очень часто в различных алгоритмах объем вычислений растет с увеличением числа многоугольников, для описания поверхностей выгодно использовать многоугольники более чем с тремя сторонами. Эти многоугольники могут быть как невыпуклыми так и неплоскими.

Мартин Ньюэл предложил способ, который позволяет найти как точное решение для плоских многоугольников, так и "наилучшее" приближение для неплоских. Этот метод эквивалентен определению нормали к каждой вершине многоугольника посредством векторного произведения прилежащих ребер и усреднения результатов. Если a, b, c, d коэффициенты уравнения плоскости, то:

(4.25)

где n - число вершин многоугольника;

если i = n, тогда j= 1, иначе j = i + 1, а значение d вычисляется с помощью любой точки на плоскости.

4.4.3 Бикубические поверхности

Описание кривых осуществляется бикубическими уравнениями (полиномы третьей степени в параметрической форме):

(4.26)

Широко используются три способа описания параметрических кубических кривых. Метод Эрмита, в котором задаются положения конечных точек кривой и касательные векторы в них. Метод Безье, в котором задается положение конечных точек кривой, а для неявного задания касательных используются две другие точки, обычно лежащие не на кривой. Метод В-сплайнов, при котором конечные точки лежат не на кривой, в результате чего как первая, так и вторая производные оказываются непрерывными на концах сегмента.

Примечание: Термин "В-сплайн" происходит от длинной тонкой металлической рейки, с помощью которых чертежники размечают поверхность самолетов и кораблей. Металлические сплайны, если они не сильно напряжены, также обладают непрерывностью второго порядка.

Рассмотрим аппроксимацию кривых с использованием В-сплайнов. При интерполяции В-сплайнами характерны два основных момента:

1. В общем случае кривая не проходит точно через заданные точки, она только использует их для формирования гладкой кривой. Чем ближе друг к другу расположены заданные точки, тем лучше будет аппроксимация, поэтому, если полученная кривая В-сплайна не очень хороша, ее можно улучшить заданием большего количества точек.

2. Самая первая и самая последняя точки не включаются в состав кривой. Отсюда следует, что для В-сплайна необходимо задавать по крайней мере 4 точки А,В,С,D. В этом случае результирующая кривая будет располагаться примерно между точками В и С. Хотя точки А и D не охватываются, они влияют на формируемую кривую, так что их нельзя опускать.

Если N - количество интервалов между двумя последовательными заданными точками, то для m заданных точек выходной файл будет содержать k точек:

k = (m - 3) N + 1 (4.27)

Количество сегментов кривой будет составлять (m - 3) и, соответственно, будет существовать ( m - 3) кубических уравнений (4.24).

В каждом сегменте кривой, лежащем между точками i и (i + 1), переменная t изменяется от 0 до 1, т.е. при t = 0 имеем конечную точку сегмента вблизи точки i, а при t = 1 производится аппроксимация точки (i + 1).

Рис. 4.9 В - сплайн

Для каждого сегмента кривой между точкой i и точкой (i + 1) можно вычислить коэффициенты ( j = 0,1,2,3 ) по значениям координат четырех соседних точек, а именно точек (i - 1), i, ( i + 1), (i + 2). Последующие выражения для вычисления коэффициентов В-сплайна приводятся без выводов:

Бикубические поверхности задаются кубическими уравнениями от двух переменных s и t. Изменяя оба параметра от 0 до 1 можно определить все точки на куске поверхности. Уравнение для (s,t x) :