Тема 6. Показатели вариации Решение типовых задач

Пример 6.1. Имеются выборочные данные о стаже работы работников коммерческих банков:

Группы работников предприятия по стажу, лет	Среднесписочная численность работников, чел. f
До 3 3-5 5-7 7-9 9 и выше	10 48 28 10 4
Итого	100

Решение. В примере представлен интервальный ряд распределения, поэтому первоначально необходимо найти середину каждого интервала. Так как, данные в примере сгруппированные, среднюю рассчитаем по средней арифметической взвешенной, дисперсию по формуле для сгруппированных данных. Все промежуточные расчеты произведем в таблице.

Таблица 6.1

Группы работников предприятия по стажу, лет	Среднесписочная численность работников, чел. f	Середина интервала х
До 3 3-5 5-7 7-9 9 и выше	10 48 28 10 4	2 4 6 8 10	20 192 168 80 40	-3 -1 1 3 5	9 1 1 9 25	90 48 28 90 100
	100		500			356

1.Средний стаж работников

лет

2.Дисперсия

3.Среднее квадратическое отклонение

4. Коэффициент вариации.

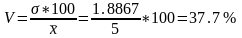
Степень вариации составляет 37,7%, это больше минимального значения коэффициента вариации = 33,0%. Чем больше коэффициент вариации, тем менее однородна совокупность и тем менее типична средняя, тем менее она характеризует изучаемое явление. И, наоборот, чем коэффициент вариации меньше, тем однороднее совокупность, тем точнее средняя отображает значение варьирующего признака, для которого она вычислена.

Пример 6.2. Имеются следующие данные о распределении 20 предприятий одной отрасли по стоимости основных производственных фондов. Рассчитайте дисперсию способом квадратов.

Группы предприятий по размеру основных производственных фондов, млн. сом	Число предприятий f
4-6 6-8 8-10 10-12 12-14	2 3 5 6 4
Итого	20

Решение. Так данные в примере сгруппированные, рассчитаем дисперсию способом квадратов по следующей формуле:

Все расчеты произведем в таблице 6.2

Таблица 6.2

Группы предприятий по размеру основных производственных фондов, млн. сом	Число предприятий f	Середина интервала х	x*f	х2	х2*f
	1	2	3	4	5
4-6 6-8 8-10 10-12 12-14	2 3 5 6 4	5 7 9 11 13	10 21 45 66 52	25 49 81 121 169	50 147 405 726 676
Итого	20	-	194		2004

Подставим значения в формулу

Пример 6.3. Имеются следующие данные о группировке предприятий по стоимости основных производственных фондов. Рассчитайте дисперсию способом отсчета от условного нуля.

Группы предприятий по размеру основных производственных фондов, млн. сом	Число предприятий f
4-6 6-8 8-10 10-12 12-14	2 3 5 6 4
Итого	20

Решение. Рассчитаем дисперсию способом отсчета от условного нуля

Для осуществления расчета по написанной выше формуле нужно избрать величину А. Это произвольная постоянная величина. Формально А можно брать любой величины. Целесообразно же в качестве такой величины брать значение признака, находящееся в середине ранжированного ряда. Только в этом случае достигается максимальное облегчение вычислительных операций. Этот способ применяется для рядов с равными интервалами. В нашем ряду значений х в середине находится число 9. Примем: А=9 (иногда вместо А пишут х_0, называя его условным началом отсчета или условным нулем). Теперь будем последовательно производить требуемые вычисления и записывать в соответствующих графах вспомогательной таблицы 6.3.

Находим разности х-А. Делим их на i (на ширину интервала). Делим вычисленные разности на i и записываем в графу 5. Эта графа показывает, какого упрощения чисел мы добились. Возводим числа гр. 5 во вторую степень и записываем в гр. 6. Взвешиваем и фиксируем результаты в гр. 7. В итоге этой графы мы получили числитель формулы.

Таблица 6.3

Группы предприятий по размеру основных производственных фондов, млн. сом	Число предприятий f	Середина интервала х	x*f	x-a (a=2)
	1	2	3	4	5	6	7
4-6 6-8 8-10 10-12 12-14	2 3 5 6 4	5 7 9 11 13	10 21 45 66 52	-4 -2 0 2 4	-2 -1 0 1 2	4 1 0 1 4	8 3 0 6 16
Итого	20	-	194	-	-	-	33

Рассчитаем среднее значение

Теперь мы располагаем всеми данными для расчета дисперсии.

σ²= 33/20*2²- (9,7-9)² = 6,11

Пример 6.4. Совокупность разбита на 2 группы: 1 группа – производительность труда рабочих ночной смены, 2 группы – производительность рабочих дневной смены.

Ночная смена			Дневная смена
Номер бригады	Производительность рабочего, шт	Количество рабочих		Номер бригады	Производительность рабочего, шт	Количество рабочих
1 2 3	20 22 25	100 50 50		4 5 6	30 35 40	100 150 50

Рассчитайте тесноту связи между производительностью рабочего и сменой с помощью эмпирического корреляционного отношения.

Решение. Определяем для каждой группы среднюю производительность по средней арифметической простой и дисперсию по формуле для несгруппированных данных, так как нам представлен дискретный ряд распределения.

Все необходимые расчеты произведем в расчетной таблице.

Таблица 6.4 Расчетная таблица для 1 группы.

Ночная смена
х1	f1	x1f1
20 22 25	100 50 50	2000 1100 1250	-1,75 0,25 3,25	3,1 0,0625 10,56	306,25 3,13 528,13
	200	4350			837,5

Средняя производительность по 1 группе (ночная смена)

Дисперсия для ночной смены (1 группа):

Таблица 6.5 Расчетная таблица для 2 группы.

Дневная смена
х2	f2	х2f2
30 35 40	100 150 50	3000 5250 2000	-4,2 0,8 5.8	17,64 0,64 57,76	1764 96 1682
	300	10250			3542

Средняя производительность по 2 группе

Дисперсия для 2 группы

Определим среднюю из групповых дисперсий. Она определяется по формуле для сгруппированных данных, потому, что численность рабочих в 2 сменах разная (200 и 300).

=8.76

Рассчитает общую для двух групп среднюю

Находим межгрупповую дисперсию, так же по взвешенной формуле

Находим общую дисперсию по правилу сложения дисперсий

Эмпирическое корреляционное отношение

=0,9

На основании эмпирического корреляционного отношения можно сделать вывод, что связь между производительностью рабочих и сменной довольно сильная.

Пример 6.5. По данным выборочного обследования заработной платы работников бюджетной сферы получены следующие показатели:

Отрасль	Средняя заработная плата, сом	Численность работников, чел. f	Дисперсия заработной платы
Здравоохранение Образование	600 800	80 120	4900 16900

Определить:

1. среднюю заработную плату работников по двум отраслям;

2. дисперсии заработной платы; а) среднюю из групповых дисперсий; б) межгрупповую дисперсию.

3. Коэффициент детерминации и эмпирическое корреляционное отношение.

Решение. 1. Средняя заработная плата работников по двум отраслям равна:

2. а) Средняя из групповых дисперсий равна

б) межгрупповая дисперсия равна

=

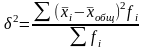в) Применяя правило сложения дисперсий, получим общую дисперсию:

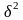= + ,=12100+9600=21700

3. а) Коэффициент детерминации равен

= или 44,24%

Он показывает, что оплата труда на 44, 24% зависит от отраслевой принадлежности работников и на 55,76% - от внутренних причин.

б) Эмпирическое корреляционное отношение

=

Что свидетельствует о существенном влиянии на дифференциацию заработной платы отраслевых особенностей.