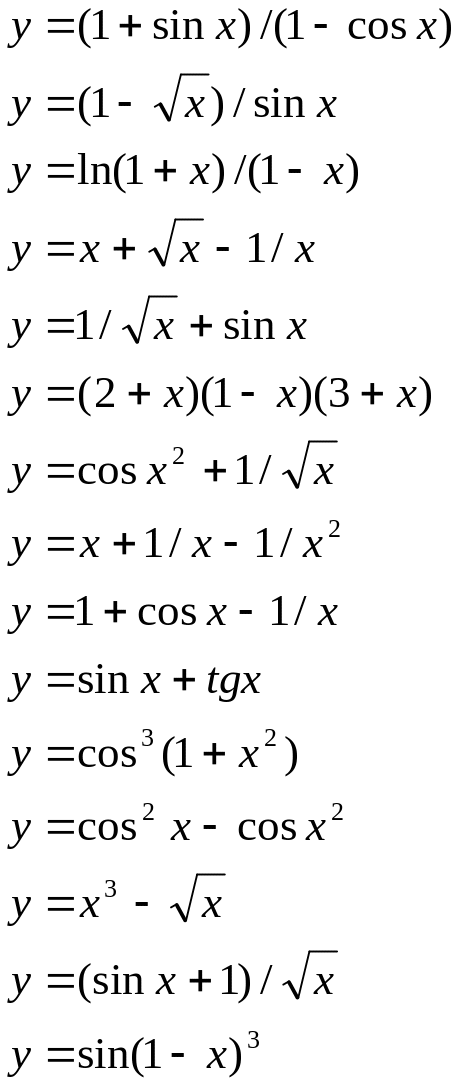6.2. Алгоритмічна та програмна реалізація інтерполяційного полінома Лагранжа

Функція задана множиною точок з координатами х_і і у_і (і=0,…n):

Х	x0	x1	x2	………	xn
Y	y0	y1	y2	………	yn

Обчислити наближене значення функції у точці х=х_р, використовуючи для інтерполяції формулу Лагранжа.

(x_i - x_k)*L2→L2

(x_p - x_k)*L1→L1

0→L

L+L₁ / L₂→L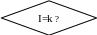

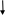
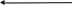
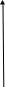
i=0, n

Y[i]→L1; 1→L2

k=0,n

Так

Ні

X_p, L

(x_p - x_k)*L1→L1

(x_i - x_k)*L2→L2

L+L₁ / L₂→L

Var Хp,L1,L2,L: real;

n,I,k: integer;

Х,У :arrary [0..30] of real;

Label M;

Begin

<Введення вихідних даних>

L:=0;

For i:=0 to n do

Begin

L1:=Y[i]; L2:=1;

For k:=0 to n do

Begin

If i=k then goto M;

L1:=L1*(Хp-Х[k]);

L2:=L2*(Х[i]-Х[k]);

M: end;

L:=L+L1/L2;

End;

<Виведення результатів>

Примітки:

1. Вихідними даними для роботи програми є масив вузлів інтерполяції Х, масив значень функції у цих точках У, кількість відрізків інтерполяції n (при цьому кількість вузлів інтерполяції n+1) і значення х=х_р, при якому обчислюється значення функції;

2. Змінні L1, L2, L використовуються для значень, відповідно, чисельника, знаменника і полінома. Вони обчислюються за формулою (6.3).

6.3. Порядок виконання роботи

1. Вибрати індивідуальне завдання. Номер варіанту у таблиці 6.1. відповідає номеру студента у списку групи;

2. Ознайомитися з теоретичним матеріалом з питань інтерполяції і апроксимації функцій;

3. Вибрати інтервал [a,b] і чотири вузли інтерполяцій в ньому х_0, х₁, х_2, і х₃, обчислити значення заданої функції у цих точках у₀, у₁, у₂, у₃. По цим даним сформувати інтерполяційний поліном Лагранжа L₃;

4. Визначити значення полінома у вузлах інтерполяції, порівняти їх з точними значеннями функції у_і;

5. Обчислити значення заданої функції і поліному при 10 значеннях х, що не співпадають з вузлами інтерполяції ( ). Визначити похибку інтерполяції у цих точках;

6. Скласти докладний алгоритм інтерполяції функції поліномом Лагранжа;

7. Скласти і відлагодити програму на мові програмування Pascal, яка реалізує введення вихідних даних; обчислення значення функції, заданої таблично, при довільному значенні n і х_р; виведення результатів у зручній формі на екран і в файл;

8. Описати алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо);

9. З використанням розробленої програми повторити пункти 4 і 5, порівняти результати;

10. Обчислити точне значення функції у трьох вибраних точках х_р1, х_р2, х_р3 ( 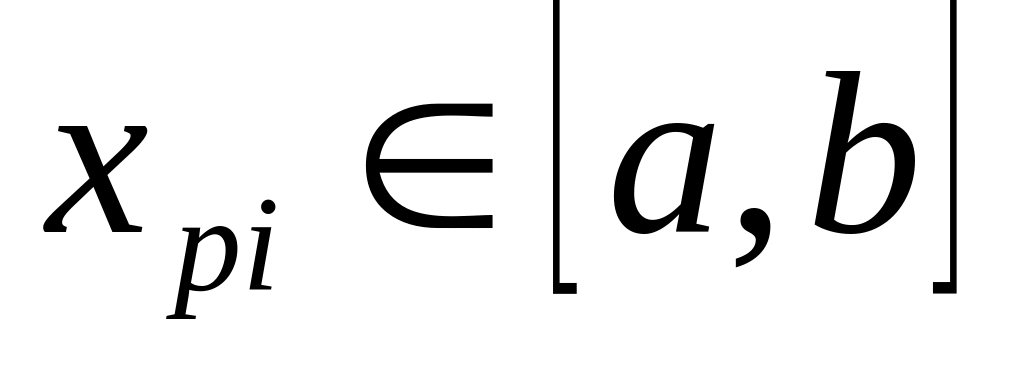) і значення поліному L_n в них (з використанням програми) при 5, 8, 10, 14, 17 і 20 вузлах інтерполяції, що розташовані в межах інтервалу [a,b]. При цьому можна використати результати п. 3 і 5.

Визначити і порівняти похибку інтерполяції.

Результати оформити у вигляді таблиці.

Побудувати графік залежності похибки інтерполяції ∆ від кількості

вузлів інтерполяції (і порядку поліному Лагранжа) n: ∆=f(n), для

кожного значення х_рі;

11. Сформулювати висновки по роботі.

Результати виконання кожного пункту завдання докладно описати у звіті по роботі.

Таблиця 6.1. Варіанти завдань до заняття № 6

Варіант	Функція	Варіант	Функція
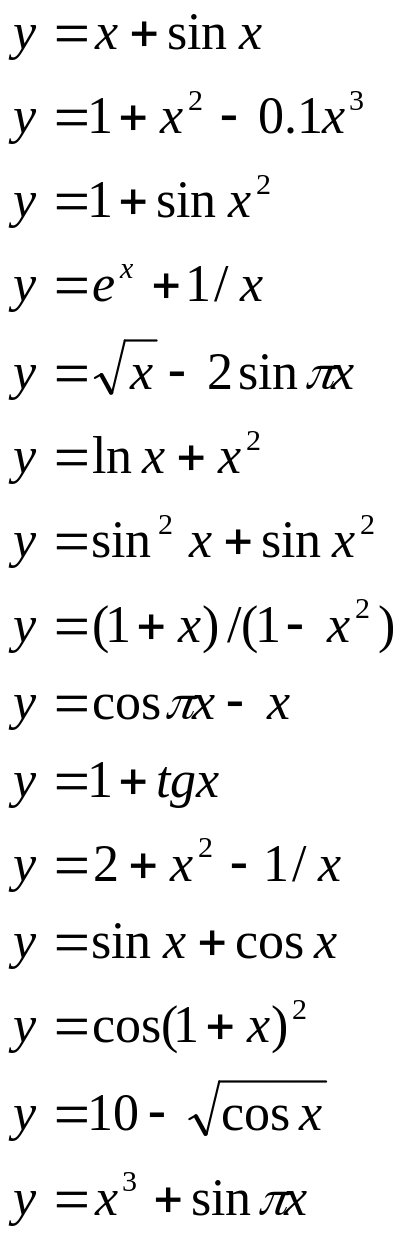
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15		16 17 18 19 20 21 22 23 24 25 26 27 28 29 30