Вступ

Комп’ютерний практикум з дисципліни “Обчислювальна техніка та програмування” проводяться зі студентами спеціальності “Системи управління виробництвом та розподілом електроенергії” у першому, другому і третьому семестрах. Відповідні методичні вказівки складаються з 4-х частин.

Зміст Частини 4 методичних вказівок до виконання комп’ютерного практикуму “Математичні методи розв’язання задач: алгоритмізація і програмування” відповідає навчальній програмі дисципліни у третьому семестрі. Тут вивчаються математичні методи розв’язання рівнянь і систем рівнянь, методи чисельного інтегрування і диференціювання функцій, інтерполяції функцій, методи розв’язання диференційних рівнянь, визначення екстремумів функцій тощо. Значна увага в методичних вказівках приділяється питанням алгоритмічної та програмної реалізації цих методів.

В результаті студенти набувають навичок самостійного розв’язання задач наукового програмування на мові Pascal.

Методичні вказівки містять матеріали 12-ти занять комп’ютерного практикуму. Матеріали кожного заняття присвячені одному із методів, що вивчаються і включають теоретичні відомості, приклади розв’язання задач, фрагменти алгоритмів і програм на мові Pascal, що реалізують відповідний метод, індивідуальні завдання і порядок їх виконання.

При виконанні завдань студент повинен ознайомитись з теоретичним матеріалом, наведеним у методичних вказівках і додатковій літературі, виконати “ручне” розв’язання індивідуального завдання, розібравшись у наведеному алгоритмі і фрагменті програми, розробити на їх основі докладний алгоритм і програму Pascal для розв’язання завдання. Після цього з використанням розробленої програми розв’язується поставлена задача і проводиться серія порівняльних розрахунків з метою дослідити характеристики математичного методу що вивчається, вплив на них різних чинників.

По результатам роботи студенти готують звіт, в якому наводять результати виконання всіх пунктів завдання.

Заняття № 1

Розробка програми

розв’язання нелінійних рівнянь методом Ньютона

Мета роботи: Закріплення знань із застосування ітераційних методів для чисельного розв’язання нелінійних алгебраїчних рівнянь, вивчення алгоритму метода Ньютона, розробка відповідної комп’ютерної програми на мові Pascal і використання її для розв’язання заданих нелінійних рівнянь.

1.1 Теоретичні відомості

Ітераційні методи. Метод Ньютона для розв’язання нелінійних

алгебраїчних рівнянь

У загальному вигляді нелінійне рівняння (алгебраїчне, трансцендентне) можна записати :

F(x) = 0 . (1.1)

Припускаємо, що функція F(x) диференціюється. Коренем рівняння (1.1) називається будь-яке значення , що обертає функцію F(x) на нуль, тобто при якому =0.

Графічно корінь рівняння відповідає значенню , при якому крива F(x) перетинає вісь абсцис:

Розв’язання рівняння заключається у визначені одного або всіх його коренів на відрізку [a,b]. Алгебраїчне рівняння n-го ступеня має не більше n дійсних коренів.

У загальному випадку нелінійні рівняння не мають аналітичних формул для визначення коренів. Тоді для їх розв’язання використовують чисельні методи, які є наближеними. Вони дозволяють знайти корені рівняння із заданою точністю.

Чисельні методи знаходження коренів рівняння складаються з двох основних етапів:

1. Визначення початкового наближення значення кореня ;

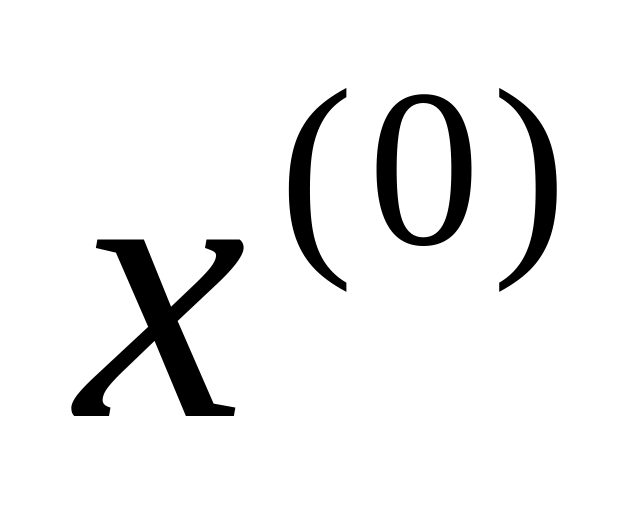2. Покрокове уточнення початкового наближення до досягнення заданої точності .

Як результат розв’язання рівняння чисельним методом приймається чергове наближення кореня , для якого виконується загальна умова :

, (1.2)

де - точне значення кореня.

Початкове наближення кореня рівняння (1.1) іноді відоме із фізичної суті задачі. Інакше його часто можна визначити , використовуючи аналіз функції F(x). При цьому підбором треба знайти такі два значення , за яких F(x) має протилежні знаки, тобто:

.

Тоді на відрізку між a і b є не менше однієї точки, де функція F(x) перетинає вісь абсцис, тобто, F(x)=0. Як початкове наближення для визначення кореня рівняння F(x) можна взяти значення:

(1.3)

Для визначення початкового наближення кореня можна застосувати, також графічне розв’язання рівнянь. Для цього треба побудувати графік функції у = F(x). Значення параметру х у точках перетину функцією вісі абсцис приймаються як початкові наближення коренів. Інший спосіб: рівняння (1.1) замінюють рівносильним рівнянням виду:

,

де функції і простіші за функцію F(x). Побудувавши графіки функцій і , початкові наближення коренів рівняння визначаємо як абсциси точок перетину цих графіків.

Чисельний метод, у якому відбувається послідовне, крок за кроком, уточнення початкового наближення, називається ітераційним методом.

Кожний крок уточнення невідомих у такому методі називається ітерацією. Якщо при послідовних ітераціях отримуємо значення, які все ближче наближуються до точного значення кореня , то такий метод ітерацій збігається.

Одним з ефективних ітераційних методів розв’язання рівнянь є метод Ньютона (метод дотичних).

Його суть полягає у заміні кривої F(x) в точці чергового наближення дотичною до неї, перетин якої з віссю x дає наступне наближення невідомого. Тут виконується лінійна апроксимація. Наступне (к+1)-ше наближення невідомого в методі Ньютона визначається за формулою:

, (1.4)

де - чергове к-те і наступне (к+1)-ше наближення невідомого;

- значення функції у точці чергового наближення (нев’язка рівняння). Визначається при підстановці у функцію;

- значення похідної функції в точці чергового наближення.

Графічна ілюстрація метода Ньютона показана на Рис. 1.1.

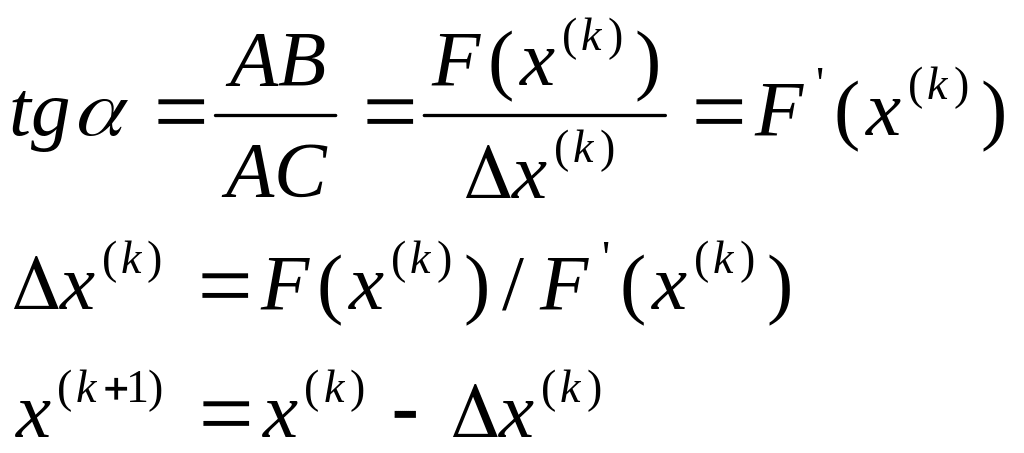
Рис. 1.1.

Примітки:

1. Як початкове наближення кореня доцільно вибрати кінець відрізку [a,b], в якому виконується умова:

(1.5)

2. Контроль завершення ітераційного процесу виконується за умовами досягнення заданої точності :

а) за зміною наближень невідомого на суміжних ітераціях:

, (1.6)

б) по величині нев’язки рівняння (1.1) на черговій ітерації:

(1.7)

Нев’язка визначається при підстановці наближення у рівняння.

3. Метод Ньютона збігається набагато швидше, ніж інші ітераційні методи.

4. Похибка округлення не накопичується – загальна властивість ітераційних методів.

Послідовність дій при розв’язанні рівняння методом Ньютона:

а) Підготовчий етап:

1. Записати рівняння у формі (1.1);

2. Визначити похідну від функції ;

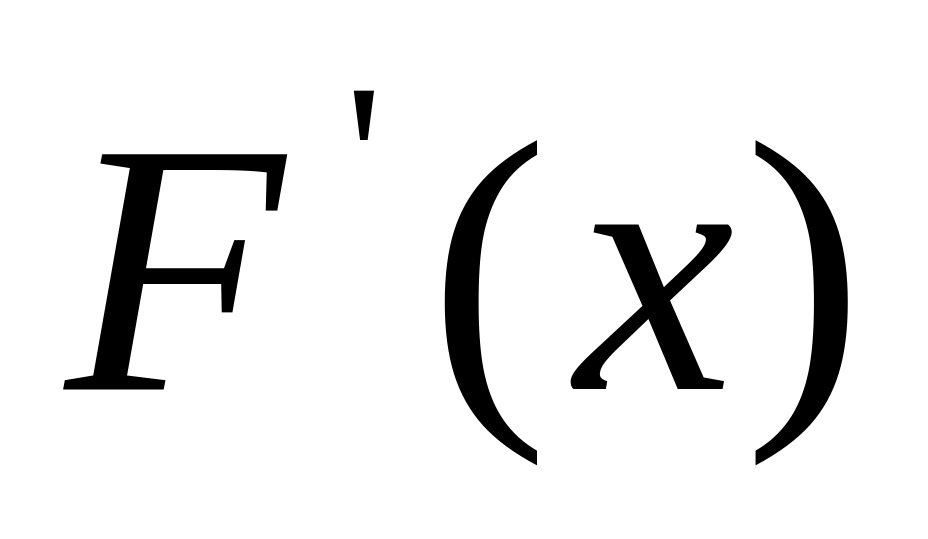3. Записати формулу (1.4) для заданого рівняння;

4. Визначити початкове наближення невідомого кореня з використанням (1.3), (1.5) тощо;

б) Розв’язання рівняння:

5. Визначити значення функції і її похідної в точці наближення;

6. За формулою (1.4) обчислити наступне наближення невідомого;

7. Перевірити умови завершення ітераційного процесу за формулами (1.6) або (1.7).

Якщо умови виконуються, то обчислене на останній ітерації наближення кореня , є розв’язком рівняння із заданою точністю .

Якщо умови не виконуються, то ітераційний розрахунок повторюється з пункту 5 при новому наближенні кореня.

Приклад розв’язання нелінійного рівняння методом Ньютона:

Знайти один із коренів рівняння з точністю

Розв’язання:

а) Підготовчий етап. Записуємо рівняння у формі (1.1):

Похідна від функції:

Запишемо формулу (1.4) для заданого рівняння:

Визначаємо початкове наближення кореня: обчислимо значення функції в точках х=2 і х=3:

.

Тобто на інтервалі [2,3] існує не менше одного кореня. Як початкове наближення можна взяти значення , при якому виконується умова (1.5).

б) Розв’язання рівняння. Ітерація 1.

.

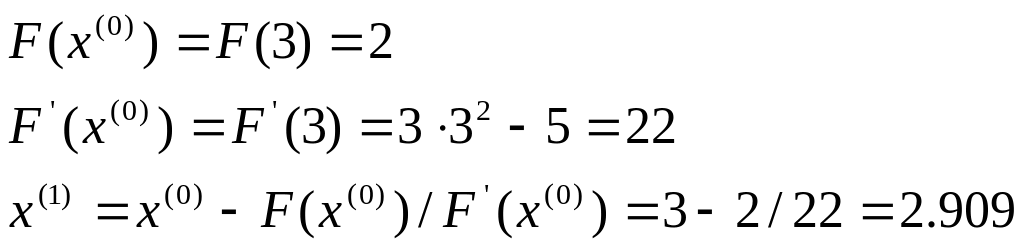Нев’язка рівняння в цій точці:

Необхідно виконати наступну ітерацію.

Ітерація 2:

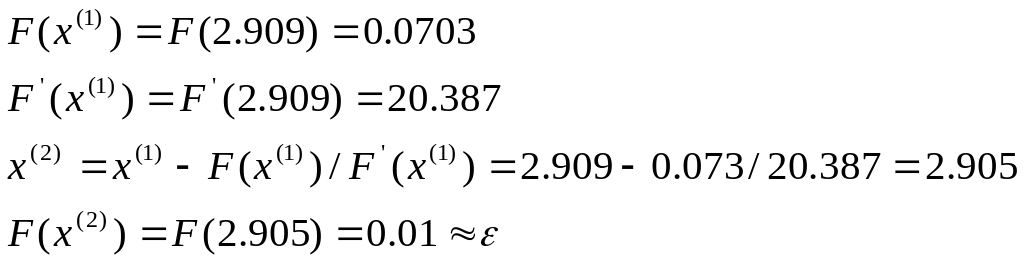
Задана точність досягнута. Як корінь рівняння із точністю приймається значення х=2.905.

1.2. Алгоритмічна та програмна реалізація метода Ньютона

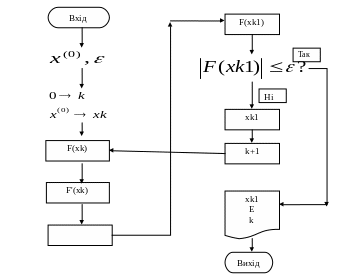
Var X0, E, XK, XK1, FK, FK1: real;

k: integer;

label M,M1;

Begin

<введення вихідних даних>

K:=0; XK:=X0;

M1: FK:=XK*XK*XK-5*XK-10;

FK1:=3*XK*XK-5;

XK1:=XK-FK/FK1;

FK:=XK1*XK1*XK1-5*XK1-10;

If abs(FK)< =E then goto M;

XK:=XK1;

K:=K+1;

goto M1;

M: <виведення результатів>

…

Примітки:

1. Фрагмент програми реалізує розв’язання рівняння, яке розглянуто у прикладі;

2. Вихідними даними є початкове наближення кореня і точність Е;

3. Результати – наближення кореня із заданою точністю ХК1, точність Е і кількість ітерацій k.

3. Порядок виконання роботи

1. Вибрати індивідуальне завдання. Номер варіанту в Таблиці 1.1. відповідає номеру студента у списку групи;

2. Ознайомитись із теоретичним матеріалом по чисельним методам розв’язання рівнянь;

3. Виконати «ручне» розв’язання заданого рівняння методом Ньютона (до 5 ітерацій);

4. Скласти докладний алгоритм розв’язання рівняння методом Ньютона;

5. Скласти і відлагодити програму на мові Pascal, яка реалізує введення вихідних даних, розв’язання заданого рівняння, виведення результатів у зручній формі на екран і в файл.

Основні фрагменти програми оформити як процедури і функції. Описати алгоритм і програму (змінні, масиви, процедури і функції, особливості реалізації тощо );

6. Розв’язати задане рівняння за допомогою розробленої програми з точністю ε =0.01. Порівняти отримані результати із результатами «ручних» розрахунків.

Побудувати графік збіжності ітераційного процесу ;

7. Обчислити корінь рівняння при 5 різних значеннях точності ( ). Контроль завершення ітераційного процесу – за умовою (1.7);

8. Повторити п.7 з використанням умови (1.6), внісши відповідні зміни у програму. Результати п.6 і п.7 оформити у вигляді таблиці;

9. Обчислити інші дійсні корені рівняння;

10. Підготувати висновки по роботі.

Результати виконання кожного пункту докладно описати у звіті по роботі.

Для отримання підвищеної оцінки необхідно на основі наведеного фрагменту програми розробити власну програму.

Таблиця 1.1. Варіанти завдань до Заняття № 1

Варіант	Рівняння	Варіант	Рівняння
1		21
2		22
3		23
4		24
5		25
6		26
7		27
8		28
9		29
10		30
11		31
12		32
13		33
14		34
15		35
16		36
17		37
18		38
19		39
20		40

Заняття № 2

Розробка програми

розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) методом Гауса

Мета роботи: Закріплення знань із застосування метода Гауса для

розв’язання СЛАР, вивчення алгоритму метода, розробка відповідної комп’ютерної програми на мові Pascal і застосування її для розв’язання заданої системи рівнянь

1. Теоретичні відомості

Метод Гауса для розв’язання СЛАР

Система n лінійних рівнянь з n невідомими у загальному вигляді може бути записана:

(2.1)

де - невідомі величини, які необхідно визначити при розв’язанні

системи;

- коефіцієнти при невідомих;

- вільні члени рівнянь системи.

У матричній формі ця система рівнянь має вигляд:

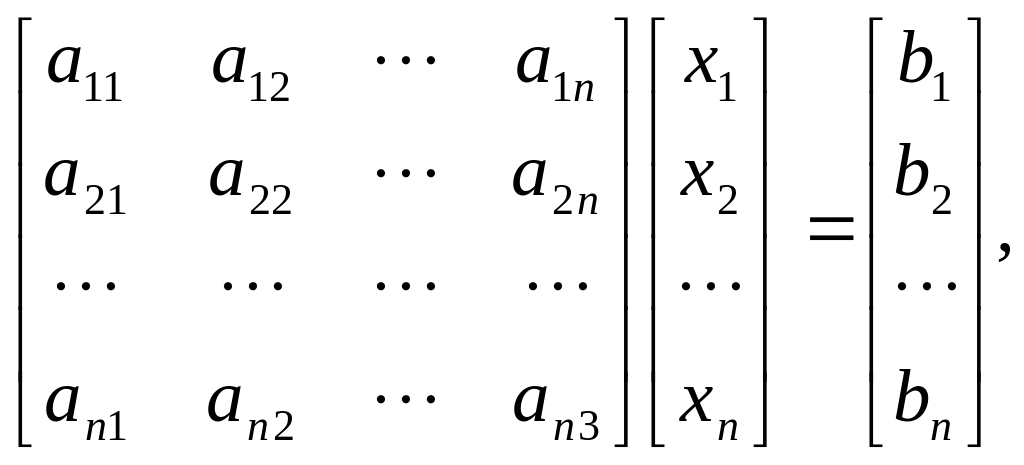(2.2)

або

де А - квадратна матриця коефіцієнтів системи розмірністю

x - вектор невідомих;

В - вектор вільних членів.

Розв’язати систему (2.1) - означає обчислити такі значення елементів вектора невідомих , за яких кожне рівняння системи перетворюється на тотожність.

Для цього можна застосувати як прямі, так і ітераційні методи. Найбільш поширеним прямим способом розв’язання систем лінійних рівнянь є алгоритм послідовного виключення невідомих, що має назву метод Гауса.

Існують різні алгоритми його реалізації. Один із них - метод Гауса із зворотнім ходом для розв’язання СЛАР розглядається у цій роботі.

Метод Гауса із зворотнім ходом передбачає виконання двох етапів: прямий і зворотній хід методу. Прямий хід - послідовність однотипних кроків виключення невідомих із системи рівнянь. В результаті його виконання вихідна система (2.1) або (2.2) з прямокутною матрицею коефіцієнтів перетворюється на еквівалентну систему рівнянь з верхньою трикутною матрицею коефіцієнтів. На зворотному ході обчислюються значення невідомих, починаючи з останнього (від до ). Розглянемо докладно можливий варіант перетворень.

Прямий хід:

Перший крок виключення невідомих. Виключаємо невідому із рівнянь системи (2.1), починаючи з другого. Виберемо на діагоналі опорний елемент a . При цьому необхідно, щоб виконувались умови:

і i=2,…n. (2.3)

Тобто він повинен бути відмінним від нуля і серед елементів першого стовпця матриці коефіцієнтів в (2.2) найбільшим за абсолютною величиною. В іншому разі переставимо рівняння в системі так, щоб ці умови виконувались.

Ділимо перше рівняння системи (2.1) на опорний елемент ;

(2.4)

Для виключення складових з невідомим із решти рівнянь необхідно рівняння (2.4) по черзі домножати на коефіцієнт і результат віднімати від відповідних рівнянь вихідної системи (2.1). В результаті отримаємо еквівалентну систему:

(2.5)

де (2.6)

номер рівняння в системі, і = 2, …, n;

j - номер елемента в рівняннях, j = 1, …, n.

На другому кроці виключення невідомих необхідно виключити з рівнянь системи (2.5), починаючи з третього. Вибираємо опорний елемент згідно з умовами, подібними до (2.3), тобто Якщо вони не виконуються, переставимо відповідним чином рівняння 2,3,…, цієї системи. Ділимо друге рівняння системи (2.5) на опорний елемент

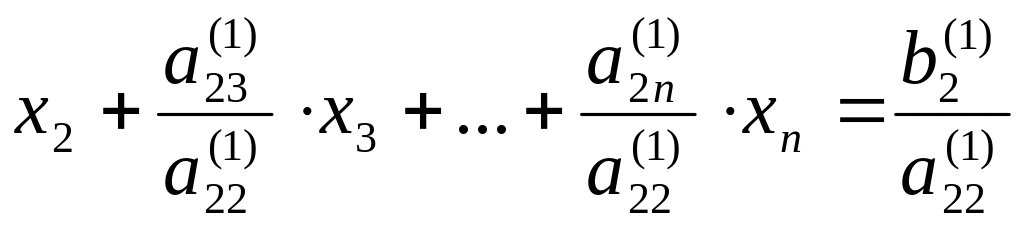. (2.7)

Виключаємо доданки з невідомим із рівнянь 3,4,…,n системи (2.5). Для цього рівняння (2.7) по черзі домножаємо на (і = 3, …, n) і результат віднімаємо від відповідних рівнянь. Отримуємо еквівалентну систему:

(2.8)

де

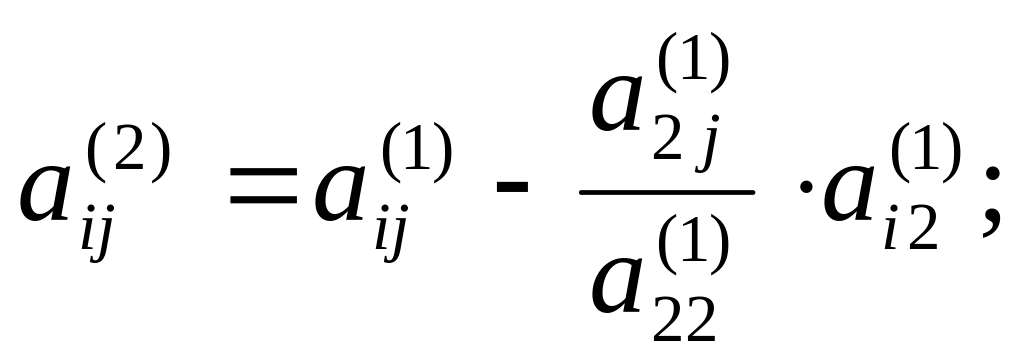
(2.9)

Наступні кроки виключення невідомих виконуються аналогічно. На k-му кроці коефіцієнти і вільні члени системи рівнянь обчислюються за такими формулами:

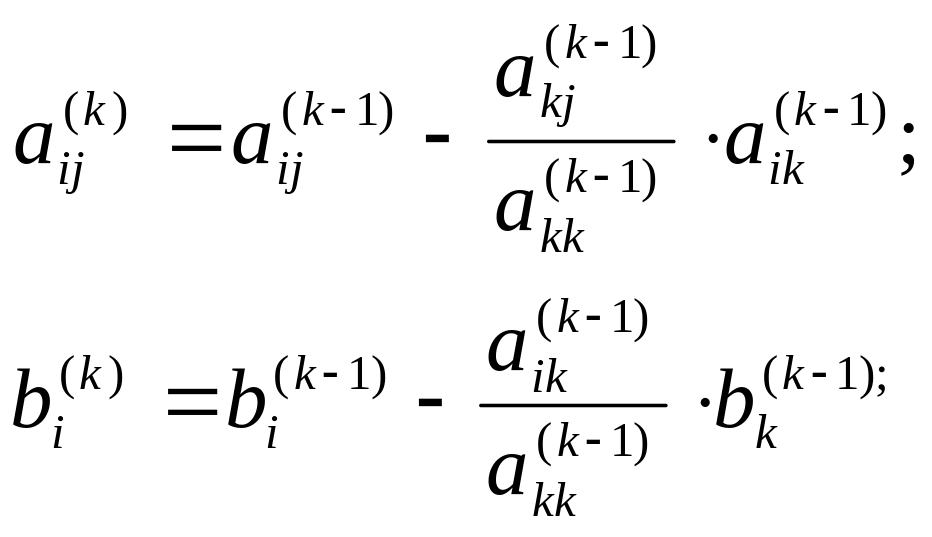, (2.10)

де к = 1, …, n-1 – номер кроку виключення невідомих, що збігається з

номером рівняння системи, в якому розташований

опорний елемент;

і = k+1, …, n - номер рівняння, з якого виключається невідома;

j = k, …, n - номер елемента в рівнянні.

Опорний елемент вибирається в стовпці відповідно до умов:

(2.11)

Після виконання останнього (n-1)-го кроку виключення невідомих вихідна система рівнянь перетворюється на еквівалентну систему з верхньою трикутною матрицею коефіцієнтів:

(2.12)

Зворотній хід:

Обчислюємо значення всіх невідомих, починаючи з . Із останнього рівняння системи (2.12) отримаємо:

(2.13)

Підставляємо його в передостаннє рівняння і обчислюємо

(2.14)

Послідовно визначаємо із решти рівнянь. Останнім обчислюється із першого рівняння при підстановці в нього всіх значень ,…, . В загальній формі ці обчислення можна описати:

(2.15)

Для перевірки правильності розв’язання системи рівнянь, необхідно обчислені значення невідомих підставити у вихідну систему (2.1). Усі рівняння повинні перетворитись при цьому на тотожності.

Приклад розв’язання СЛАР методом Гауса

Обчислити корені системи 3-х лінійних рівнянь з трьома невідомими

(2.16)

Прямий хід.

Необхідно виконати 2 кроки виключення невідомих. На першому кроці (к=1) виключаємо невідому із другого і третього рівнянь системи (2.16). Опорний елемент =5. Ділимо на нього перше рівняння системи (2.16):

і виконуємо виключення. Для цього робимо перетворення відповідно до (2.6) при і=2,3; j=1,2,3:

і=2,

Таким чином, в результаті перетворень, друге рівняння (i=2) набуває вигляду:

і=3,

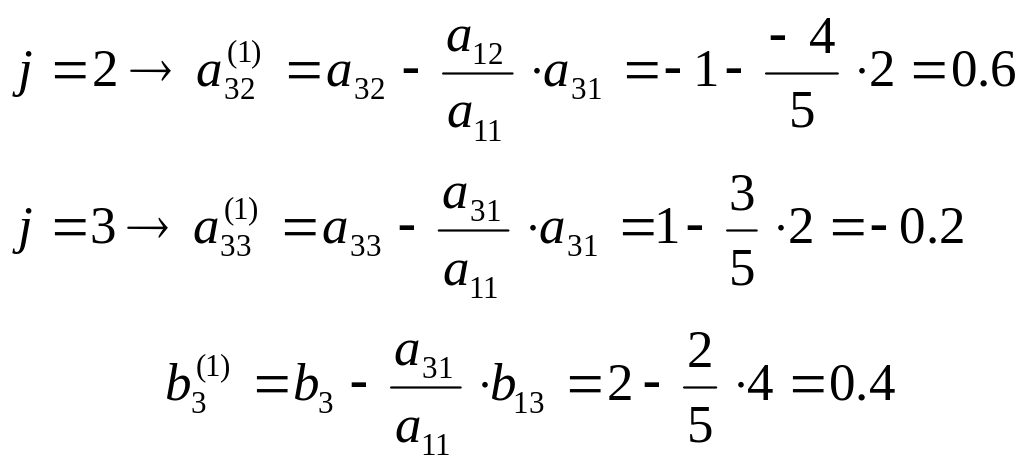
Третє рівняння (і=3) набуває вигляду:

0+0.6

Отримуємо еквівалентну систему рівнянь:

(2.17)

На другому кроці (к=2) виключаємо невідому із третього рівняння системи (2.17). Опорний елемент Ділимо на нього друге рівняння системи (2.17):

і виконуємо виключення. При і=3, j=2,3 відповідно до (2.9) отримуємо:

і=3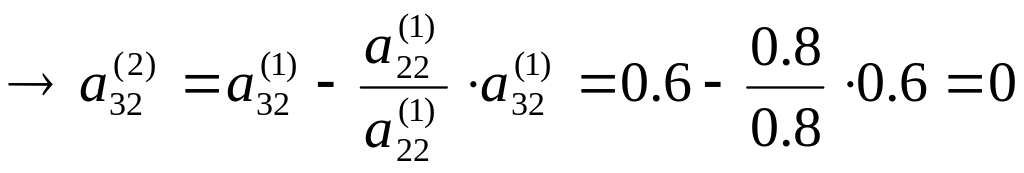

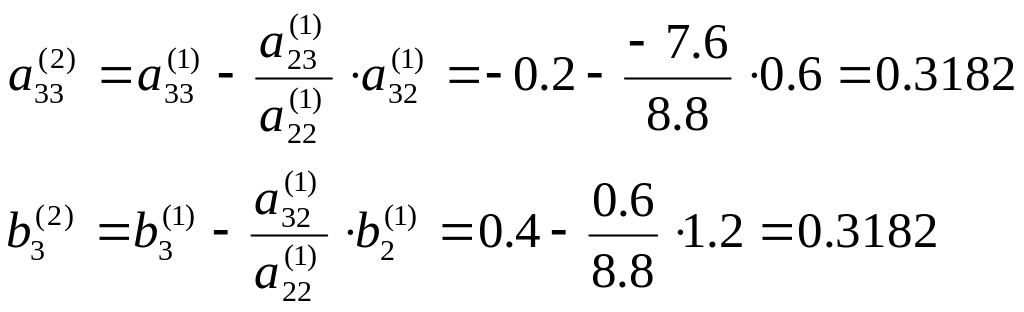
Третє рівняння системи (2.17) набуває вигляду:

0+0.3182

Отримуємо еквівалентну систему рівнянь з трикутною матрицею коефіцієнтів:

(2.18)

Зворотній хід.

Із останнього рівняння системи (2.18) знаходимо:

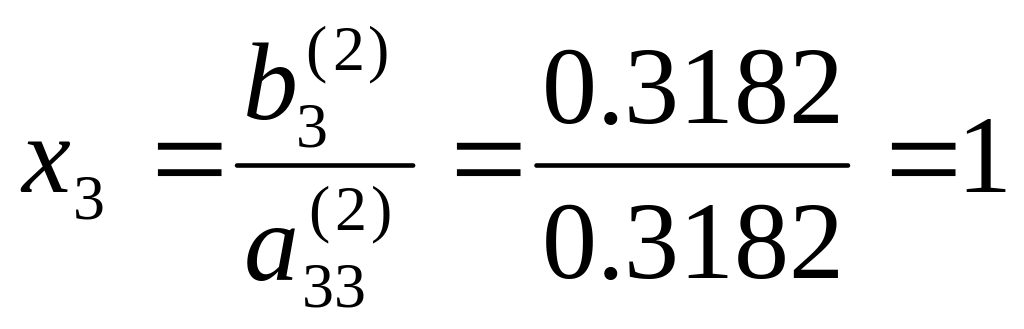
Підставляємо обчислене значення в передостаннє рівняння системи (2.18) і знаходимо:

Із першого рівняння системи знаходимо:

Таким чином, розв’язком системи є вектор

.

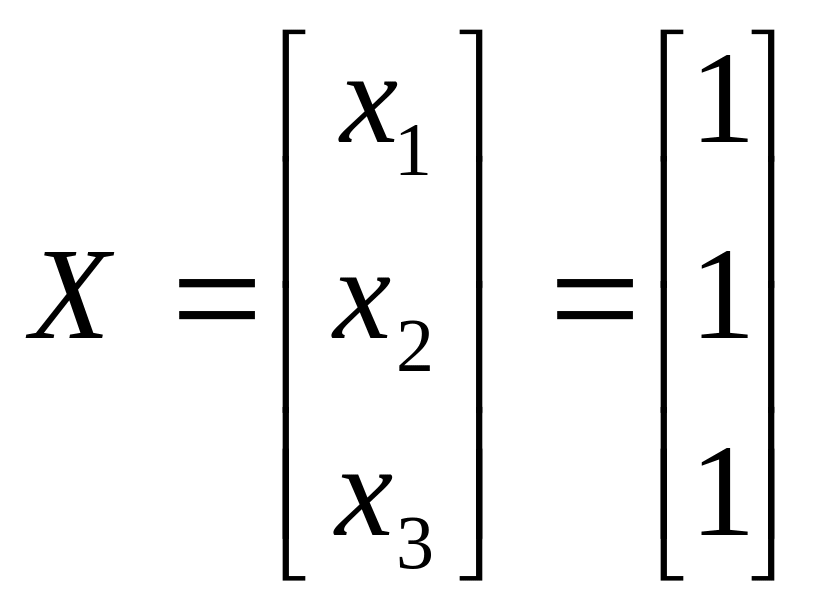Для перевірки правильності розв’язання системи рівнянь підставляємо елементи вектора Х у вихідну систему (2.16). Рівняння системи перетворюється на тотожності, що підтверджує правильність її розв’язання.