Практичне заняття №2

Тема: Векторний добуток векторів. Лінійна незалежність векторів

Література: [1,3].

Ціль: З’ясувати, які є способи обчислення векторного добутку двох векторів, як використовуються їх властивості при обчисленні, як проводити дослідження системи векторів на утворення ними базису.

План.

3. Векторний добутки векторів.

4. Лінійна незалежна система векторів.

Векторний добутки векторів.

Завдання №1. Обчислити площу трикутника, побудованого на векторах і , якщо а кут між векторами

Розв'язок:

Так як , то

.

Відповідь: Площа трикутника дорівнює .

Завдання №2. У трикутнику з вершинами . Знайти висоту .

Розв'язок: Згідно з геометричним змістом векторного добутку двох векторів маємо:

Із елементарної математики

Виразимо висоту:

Знаходимо вектори:

.

Відповідь: Довжина висоти дорівнює .

Завдання №3. Обчислити величину обертального моменту сили , прикладеної до точки відносно точки .

Розв'язок: Знайдемо координати вектора , тоді

Відповідь: Величина обертального моменту дорівнює .

Завдання №4. Довести, що чотири точки лежать в одній площині.

Розв'язок: Знаходимо вектори , і . Перевіряємо умову компланарності трьох векторів (вектори, а значить и точки, будуть лежати в одній площині) .

.

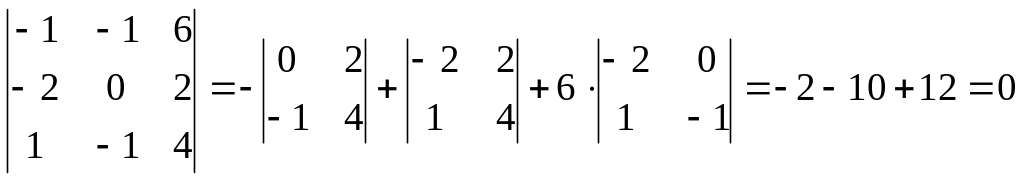Відповідь: точки належать одній площині.

Завдання №5. В тетраедрі з вершинами в точках обчислити висоту .

Розв'язок: Зробимо малюнок.

Геометричний зміст змішаного добутку трьох векторів, що виходять з однієї точки, це об’єм призми, побудованої на цих векторах. Тоді формула об’єму піраміди:

З елементарної математики відомо, що , тоді

Звідки

Знаходимо вектори .

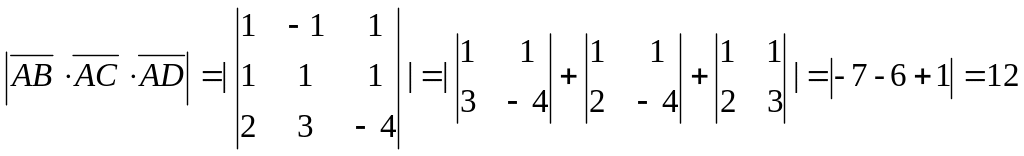
Тоді

Відповідь: Довжина висоти дорівнює .

Лінійна незалежна система векторів.

Завдання №6. Довести, що вектори , , утворюють базис і знайти координати вектора в цьому базисі.

Розв'язок: Три не компланарних вектори в – лінійно незалежні і утворюють базис по якому можна розкласти будь який четвертий вектор.

Перевіримо компланарність векторів .

Отже вектори утворюють базис. Тоді . Перепишемо в координатній формі:

Розв’яжемо цю систему методом Крамера.

, , .

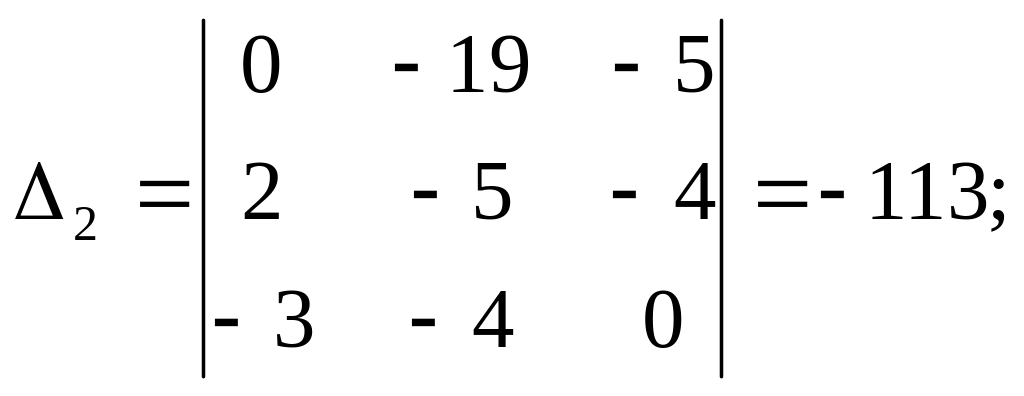
Тоді .

Відповідь: .

Завдання до практичного заняття №2

Завдання №1

У трикутнику з вершинами . Знайти висоту .

1.1	1.5
1.2	1.6
1.3	1.7
1.4	1.8

Завдання №2

Обчислити площу трикутника , якщо відомі координати його вершини.

2.1 .	2.5
2.2 .	2.6
2.3	2.7
2.4	2.8

1.3 Домашня контрольна робота (дкр) Умови виконання

1. Обчислити довжину більшої бісектриси внутрішнього кута трикутника при вершині , якщо відомі координати його вершин (1).

2. Обчислити скалярний добуток векторів і , утворених лінійною комбінацією векторів, що мають координати точок (2).

3. Обчислити площу трикутника , якщо відомі координати його вершин (3).

4. Довести, що вектори утворюють базис і знайти координати вектора в цьому базисі (4).

5. Обчислити об’єм піраміди , якщо відомі координати її вершини (5).