
- •1. Векторна алгебра
- •1.1 Теоретичні відомості
- •1.2 Практична частина Практичне заняття №1
- •Завдання до практичного заняття №1
- •Практичне заняття №2
- •Завдання до практичного заняття №2
- •1.3 Домашня контрольна робота (дкр) Умови виконання
- •Варіанти завдань до дкр
- •1.4 Теоретичні питання
- •1.5 Аудиторна контрольна робота (акр)
- •Завдання № 1
- •Завдання № 2
- •Завдання № 3
- •Завдання № 4
- •Завдання № 5
- •Завдання№ 6
- •Завдання № 7
- •Анотація до акр Тест містить сім завдань. Критерій оцінювання знань студентів визначається ваговим коефіцієнтом цих завдань:
- •Перелік кривих другого порядку
- •2.2 Практична частина Практичне заняття № 1
- •Завдання до практичного заняття № 1.
- •Приклад 2. При якому значенні с пряма
- •Приклад 3. Знайти значення параметра , при якому пряма
- •Приклад 4. Привести до нормального вигляду рівняння прямої
- •Заняття №2
- •Завдання № 1. Указати, які із прямих паралельні й перпендикулярні:
- •Завдання до практичного заняття № 2.
- •Завдання № 4.
- •Завдання № 5.
- •І віддалених від неї на відстань .
- •Заняття №3
- •Завдання до практичного заняття № 3
- •Заняття №4
- •Завдання до практичного заняття № 4
- •2.3 Домашня контрольна робота (дкр) Умови виконання
- •При якому значенні с пряма відсікає на осі Оу відрізок ?
- •Варіанти завдань до дкр
- •2.4 Теоретичні питання
- •Завдання № 6
- •Завдання № 7
- •Завдання № 8
- •Завдання № 9
- •Завдання № 10
- •Завдання № 11
- •Анотація до акр
- •Тест містить дванадцять завдань. Критерій оцінювання знань студентів визначається ваговим коефіцієнтом цих завдань:
ЗМІСТ
|
ВСТУП................................................................................................. |
4 |
|
1. ВЕКТОРНА АЛГЕБРА...……............................................... |
7 |
|
1.1 Теоретичні відомості...…………………………….. |
7 |
|
1.2 Практична частина....................................................... |
15 |
|
Практичне заняття №1.............................................................. |
15 |
|
Практичне заняття № 2............................................................ |
22 |
|
1.3 Домашня контрольна робота (ДКР)....................................... |
27 |
|
1.4 Теоретичні питання............................................................... |
36 |
|
1.5 Аудиторна контрольна робота (АКР)..................................... |
37 |
|
1.6 Приклад тесту до АКР............................................................ |
46 |
|
2 АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ… |
48 |
|
2.1 ТЕОРЕТИЧНІ ВІДОМОСТІ…………............................ |
48 |
|
2.2 ПРАКТИЧНА ЧАСТИНА...…..………………………… |
54 |
|
Практичне заняття № 1…………………………………… |
54 |
|
Практичне заняття № 2…………………………………… |
61 |
|
Практичне заняття № 3……………………………… |
68 |
|
Практичне заняття № 4…………………………….………… |
75 |
|
2.3 Домашня контрольна робота (ДКР)………………………… |
81 |
|
2.4 Теоретичні питання…………....................……………… |
93 |
|
2.5 Аудиторна контрольна робота (АКР)..…..……………… |
94 |
|
2.6 Приклад тесту до АКР……………….....…………………… |
113 |
|
ВИКОРИСТАНА ЛІТЕРАТУРА………..…………..…… |
117 |
ВСТУП
Згідно Болонського процесу в Україні відбувається трансформація освітнього та наукового простору. Невід’ємною частиною цього процесу є впровадження кредитно-модульної системи навчання.
Перелік розділів, з яких формуються модулі:
Розділ 1. Визначники та матриці;
Розділ 2. Векторна алгебра і аналітична геометрія;
Розділ 3. Аналітична геометрія в просторі;
Розділ 4. Лінійний простір та лінійні оператори;
Розділ 5. Вступ до аналізу;
Розділ 6. Диференційне числення функцій однієї змінної;
Розділ 7. Диференційне числення функцій багатьох змінних;
Розділ 8. Невизначений інтеграл;
Розділ 9. Визначений інтеграл;
Розділ 10. Диференціальні рівняння зі змінними коефіцієнтами;
Розділ 11. Диференціальні рівняння з постійними коефіцієнтами;
Розділ 12. Числові ряди та поняття функціонального ряду;
Розділ 13. Степеневі ряди і ряди Фур’є;
Розділ 14. Інтегральне числення функцій багатьох змінних;
Розділ 15. Елементи векторного аналізу;
Розділ 16. Диференційне і інтегральне числення функцій комплексної змінної;
Розділ 17. Інтегральне числення функції комплексної змінної;
Розділ 18. Операційне числення;
Розділ 19. Елементи математичної фізики;
Розділ 20. Елементи теорії ймовірностей;
Розділ 21. Елементи математичної статистики.
Оцінювання знань студентів по відповідному модулю здійснюється за допомогою комп’ютерного тестування (АКР), та захисту домашніх контрольних робіт (ДКР).
Даний методичний посібник розрахований на самостійне засвоєння студентами матеріалу розділу “Векторна алгебра і аналітична геометрія”, а також може бути використаний викладачами при проведенні практичних занять.
Посібник включає:
короткі теоретичні відомості по темам;
практичні заняття по темам;
набір тестових завдань (АКР) по першому модулю;
варіанти домашніх контрольних робіт (ДКР);
теоретичні питання для захисту ДКР студентами.
Зміст практичних завдань по темам наступний:
Тема 1. Вектори. Операції над векторами.
Тема 2. Векторний добуток векторів. Лінійна незалежність векторів.
Тема 3. Рівняння прямої на площині.
Тема 4. Умови перпендикулярності й паралельності двох прямих. Відстань від точки до прямої. Кут між двома прямими.
Тема 5. Канонічні рівняння кривих другого порядку. Формули паралельного переносу координатних осей. Полярна система координат.
Тема 6. Перетворення осей координат на площині. Формули повороту осей.
1. Векторна алгебра
1.1 Теоретичні відомості
В ектором
називається
напрямлений прямолінійний відрізок і
позначається як:
ектором
називається
напрямлений прямолінійний відрізок і
позначається як:
![]() ,
де
,
де
![]() - початок, а
- початок, а
![]() - кінець вектора, або однією буквою
- кінець вектора, або однією буквою
![]() (Рисунок.1.1)
(Рисунок.1.1)
Рисунок 1.1
При
цьому довжина відрізка називається
модулем
вектора
і позначається символом
![]() або
або
![]() .
.
Якщо
початок відрізка співпадає з його
кінцем, то вектор називається нульовим
![]() .
.
Вектори називаються колінеарними, якщо вони лежать на одній прямій, або на паралельних прямих.
На відміну від фізичних векторів у математиці розглядаються вільні вектори, тобто вони визначені з точністю до точки прикладення.
Два
вектори
і
![]() називаються
рівними
називаються
рівними
![]() ,
якщо:
,
якщо:
вони колінеарні
 ;
;мають однакову довжину
 і напрямлені в одну сторону.
і напрямлені в одну сторону.
Лінійні операції над векторами це – додавання векторів по правилу трикутника або паралелограма та добуток вектора на дійсне число.
Проекція
вектора
на вісь
![]() дорівнює:
дорівнює:
![]() ,
,
де
![]() - кут між вектором та віссю
.
Тоді , користуючись лінійними операціями
над векторами, у прямокутній системі
координат маємо:
- кут між вектором та віссю
.
Тоді , користуючись лінійними операціями
над векторами, у прямокутній системі
координат маємо:

де
![]() - одиничні вектори
- одиничні вектори
![]() направлені по осям
направлені по осям
![]() .
.
![]() - проекції вектора
на відповідні осі координат.
- проекції вектора
на відповідні осі координат.
Легко
показати, що модуль вектора
![]() ,
направляючі косинуси:
,
направляючі косинуси:

де
![]() - кути між вектором і відповідними осями
координат.
- кути між вектором і відповідними осями
координат.
Якщо
![]() і
і
![]() ,
то
,
то
![]() ,
,
![]() .
.
Умова
колінеарності двох векторів
і
це
![]() .
.
Координатами
![]() -мірного
вектора
-мірного
вектора
![]() є
дійсних чисел
є
дійсних чисел
![]() .
Сукупність
векторів
.
Сукупність
векторів
![]() називається лінійно
незалежною, якщо
рівняння:
називається лінійно
незалежною, якщо
рівняння:
![]()
виконується
тільки при умові, що всі
![]() .
Система
лінійно незалежних векторів утворює
базис у
-мірному
просторі по якому можна розкласти
будь-який
.
Система
лінійно незалежних векторів утворює
базис у
-мірному
просторі по якому можна розкласти
будь-який
![]() вектор.
вектор.
Дії над векторами можна зобразити у вигляді таблиці.
Означення та формули |
Приклади |
1. Якщо
|
1)
Вектор
або
Вектор
|
2. Сумою
або різницею
двох векторів
Добутком
вектора
на дійсне число
|
1)
Знайти
Розв'язок:
Відповідь:
|
3.
Скалярним
добутком двох
векторів
і
називається число
Якщо
умова ортогональності двох векторів. В координатній формі:
і
|
1)
Обчислити роботу виконаною силою
Робота
знаходиться
по формулі:
2)
Знайти, при якому
вектори
3)
Знайти вектор
Розв’язок:
Відповідь:
|
4
Рисунок. 1.2
Якщо
вектори
і
задані в координатній формі, тобто
згідно
властивості а), площу трикутника з
вершинами
Якщо
|
1)
Визначити, при яких значеннях
Відповідь:
2)
Знайти координати вектора
,
якщо він перпендикулярний векторам
Розв’язок:
Тоді
3)
Обчислити площу трикутника з вершинами
Розв’язок:
Знайдемо
координати векторів
Відповідь:
|
5. Змішаний добуток трьох векторів. Послідовний добуток трьох векторів , , можна здійснити різними способами. Наприклад, можна вектори і перемножити векторно і отриманий вектор перемножити скалярно на вектор :
В результаті отримаємо число, що відповідає змішаному добутку трьох векторів. Враховуючи геометричний зміст скалярного і векторного добутків, це число означає об’єм призми, побудованої на векторах , і .
Тоді
об’єм трикутної піраміди з вершинами
у точках
Якщо
змішаний добуток трьох не нульових
векторів дорівнює нулю, то вони лежать
в одній площині, або в паралельних і
називаються компланарними,
тобто
|
1)
Обчислити об’єм піраміди
Знайдемо
координати векторів
Тоді об’єм піраміди дорівнює:
Відповідь:
2) При
якому
вектори
Умова компланарності
3)
Довести, що чотири точки
Знаходимо
вектори
Відповідь:
точки
|
6. Умова
лінійної незалежності системи векторів.
Якщо
визначник із координат векторів не
дорівнює нулю, то такі вектори лінійно
незалежні і утворюють базис для даного
простору. Будь які два не колінеарні
вектори утворюють базис в
|
1)
Довести, що вектори
,
і
утворюють базисі знайти координати
вектора
в цьому базисі, якщо
Перевіряємо умову компланарності:
Утворюють базис в , тоді:
В координатній формі маємо
Для
знаходження
Тоді
Відповідь: . |



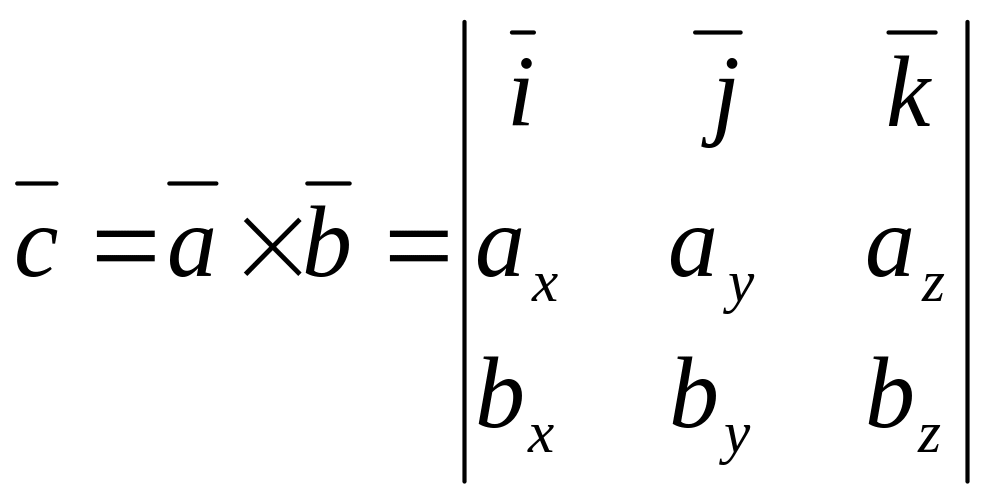 .
.




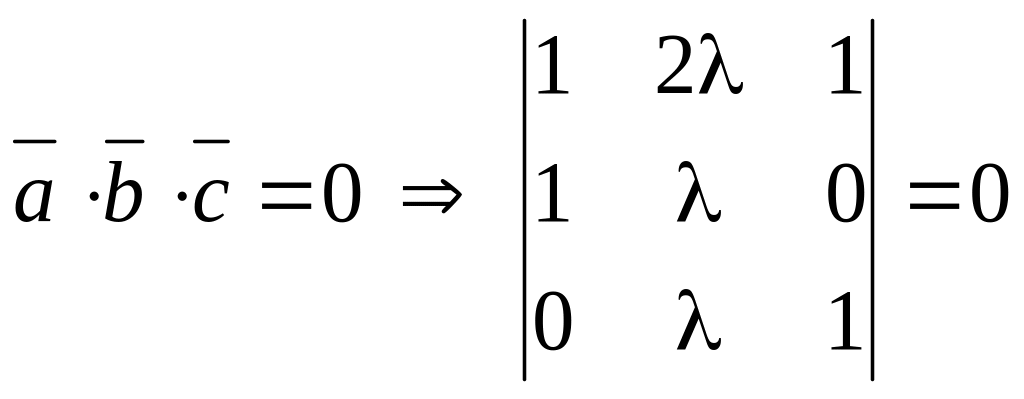


 .
.

