семинар 1

СЕМИНАР 1

Фазовое равновесие в однокомпонентных системах. Процессы испарения и возгонки

Прежде чем начать рассмотрение задач, необходимо познакомиться с таблицей, содержащей основные справочные материалы по данной теме. Это таблица 24 (стр. 30

– 35 справочника А.А. Равделя).

В ней приведены температуры фазовых превращений (испарения и возгонки) различных веществ при разных внешних давлениях. Под температурами возгонки можно увидеть пометку (кр.), то есть речь идет о кристаллическом веществе. Например, для брома:

1

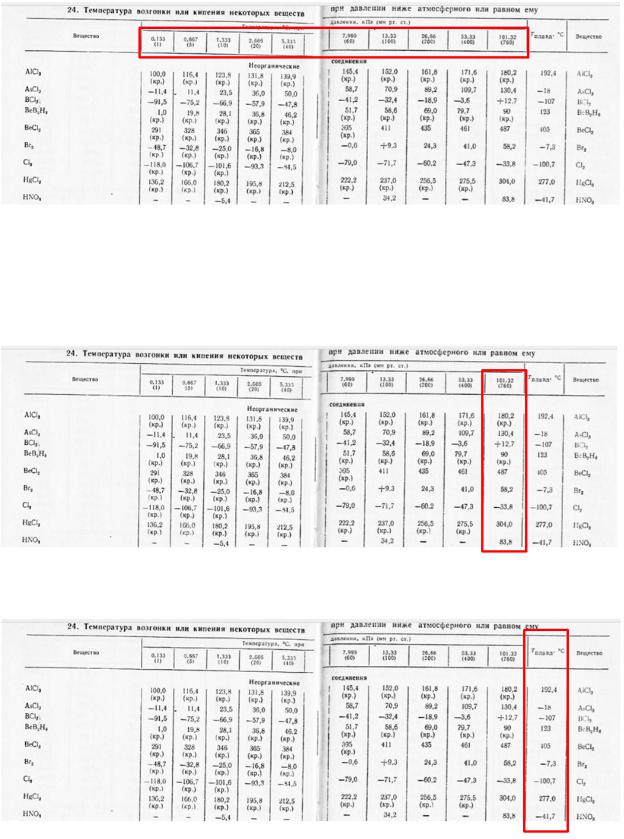
С другой стороны, из таблицы можно узнать давление насыщенного пара (в кПа или мм рт.ст.) над жидкой или твердой фазой при разных температурах:

Нормальные температуры кипения веществ находятся в крайнем правом столбце и соответствуют атмосферному давлению (101,32 кПа или 760 мм рт.ст.).

Последний столбец таблицы содержит температуры плавления.

И если температур возгонки и испарения для каждого вещества несколько, так как они зависят от давления, то температура плавления только одна (от давления практически не зависит, и ее можно относить к любому внешнему давлению).

2

Задача 3

В задаче требуется найти изменение энтропии и внутренней энергии при испарении вещества. Уравнение Клапейрона-Клаузиуса позволяет найти теплоту испарения. Поэтому, прежде чем вычислять другие термодинамические функции, сначала необходимо найти ∆исп .

Так как в условии сказано, что «теплоту испарения в интервале температур можно считать постоянной», то тепловой эффект ищем именно средний, используя интегральную форму уравнения Клапейрона-Клаузиуса:

= ∆исп 1 − 1

или

∆исп = −

Для использования этой формулы необходимы две пары данных (давления насыщенного пара жидкости при двух разных температурах). В условии явно нет этих значений, но есть отсылка к справочным данным. Поэтому давления и температуры мы будем брать из таблицы 24, стр. 30 (справочник А.А. Равделя). Кроме того, в условии задан приблизительный температурный интервал температур, на который мы должны ориентироваться для выбора данных из справочника. Наиболее близкие температуры в справочнике (и

соответствующие им давления):

Именно их мы и подставим в расчетную формулу (не забывая переводить

На следующем этапе рассчитаем изменение энтропии при заданной указанной температуре 27 :

3

∆исп = ∆исп исп

исп = 27 исп = 27 + 273 = 300 К

Это изменение энтропии при испарении 1 моль вещества. В условии задано другое количество, а именно 1,5 моль. Учитываем это:

Для расчета внутренней энергии испарения воспользуемся формулой связи изобарного и изохорного тепловых эффектов:

∆исп = 43931,25 − 1 ∙ 8,314 ∙ 300 = 41437,05 Дж/моль

Внимание! Для обратных фазовых переходов абсолютные значения термодинамических функций остаются такими же, но знак меняется на

противоположный. Например, для конденсации:

∆конд = −∆исп

∆конд = −∆исп

∆конд = −∆исп

∆конд = −∆исп = −1

Задачи для самостоятельного решения: № 1, 2, 4, 5, 6, 7

4

Задача 8

В данной задаче требуется найти теплоту испарения при заданной температуре, т.е. истинный тепловой эффект. В основе расчета лежит дифференциальная форма уравнения Клапейрона-Клаузиуса:

= ∆исп

откуда можно выразить тепловой эффект:

Вид уравнения аналогичен виду дифференциальной формы уравнения

изобары Вант-Гоффа. И нахождение истинной теплоты испарения проводится по той же схеме, что и расчет истинного теплового эффекта реакции, а именно:

Вусловии дана функциональная зависимость:

=− 3308 + 10,373 − 0,8 ∙

Действуем по предложенной схеме:

2,303 ∙ = −2,303 ∙ 3308 + 2,303 ∙ 10,373 − 2,303 ∙ 0,8 ∙

=−2,303 ∙ 3308 + 2,303 ∙ 10,373 − 0,8 ∙

=+2,303 ∙ 3308 + 0 − 0,8

5

Учитываем количество вещества:

Расчет энтропии проводится аналогично расчету в задаче 3:

∆исп = ∆исп исп

Задачи для самостоятельного решения: № 9, 10.

6

Задача 11

В этой задаче также требуется найти энтальпию (теплоту) испарения вещества при определенной температуре, т.е. истинный тепловой эффект. Используем дифференциальную форму уравнения Клапейрона-Клаузиуса:

Для того, чтобы найти значение производной , продифференцируем по

температуре данную в условии зависимость:

= 0 − 3,37 ∙ 10 − 2 ∙ 80,11 ∙

Подставим значение температуры:

=−10

=−10 + 273 = 263 К

Теперь можно найти теплоту испарения:

7

В условии не упоминается количество вещества, поэтому рассчитываем изменение энтальпии на 1 моль.

Задача для самостоятельного решения: № 12.

Задача 17

В условии даны две зависимости: первая представляет собой зависимость

Уравнение (1) описывает линию возгонки ОВ, уравнение (2) – линию испарения ОА. (Данные в условии зависимости включают в себя десятичный логарифм, но он может быть преобразован в натуральный домножением на 2,303, и вид графика от этого не изменится.)

8

Тройная точка О является точкой пересечения описываемых кривых.

Поэтому для нахождения ее координат надо решить систему уравнений для общих значений и , соответствующих давлению и температуре тройной точки:

т.т. = 12,486 − 3160

12,486 − 3160 = 7,884 − 1860

т.т. т.т.

Подставляем найденное значение температуры в одно из уравнений и находим значение давления:

Для нахождения теплоты плавления вспомним связь между тепловыми эффектами фазовых переходов: испарения, плавления и возгонки:

9

∆возг = ∆исп + ∆пл

Отсюда теплота плавления:

∆пл = ∆возг − ∆исп

Теплоты испарения и возгонки можно найти из уравнений (1) и (2), сопоставив их с уравнением линейной зависимости, которое в общем виде записывается следующим образом:

Теперь, зная теплоту плавления, можно найти энтропию плавления:

Задачи для самостоятельного решения: № 16, 18.

10