2.3. Практикум по материальным запасам
Задача. Строительная фирма «Керамстрой» приобретает керамическую плитку по цене 80 долл. за 1 . Потребность в год равна 6400 . Цена капитала фирмы составляет 16 %. Складские расходы – 3,2 долл. на 1 в год. Стоимость заказа партии – 200 долл. Определить оптимальный размер партии, количество заказов в год, логистические затраты.
Решение. Для определения оптимальной партии необходимо обладать информацией о затратах на хранение единицы материала на складе. По условию известны складские расходы и расходы, связанные с замораживанием финансовых средств, сумма которых и является затратами на хранение материалов, которые можно определить следующим образом:
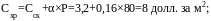
где
–
затраты на хранение единицы материала;
–
складские расходы; Р – цена единицы
материала; α – процентная ставка.
Величину размера оптимальной партии определим по формуле Уильсона
где S – размер партии; – транспортно-заготовительные расходы на единицу материала; Q – величина оборота за определенный период времени; – тариф на хранение единицы материала.
Количество заказов в год
,
где n – количество заказов; Q – величина оборота за определенный период времени; S – размер партии.
Логистические затраты можно определить как сумму затрат на хранение и затрат на транспортирование:
где
S – размер партии;
– транспортно-заготовительные расходы
на единицу материала; Q – величина
оборота за определенный период времени;
– тариф на хранение единицы материала.
Итак, для достижения минимального уровня затрат на управление материалами следует делать 8 закупок по 400 керамической плитки.
Задача.
Строительная компания имеет потребность
в плитке 1 млн.
на
год. Поставщик плитки представляет
товар цена которого зависит от размера
партии. Затраты на содержание запасов
компании так же зависят от размера
хранимой партии. Затраты на заказ партии
не зависят от размера заказываемой
партии. Определить логистические затраты
и оптимальный размер партии. Построить
график определения оптимального размера
партии, если известно, что затраты на
заказ партии 350 у.е. (
),
затраты на содержание запасов у.е. на
кв. м. (
)
зависят от размера партии: если размер
партии от 1 до 10000, то затраты 5 у.е.; если
размер партии от 10001 до 19999, то затраты
4 у.е.; если размер партии более 20000 , то
затраты на единицу 1.6 у.е. Цена материала
так же зависит от размера партии: если
размер партии от 1 до 10000 , то цена 0,05
у.е.; если размет партии от 10001 до 19999, то
цена 0,042 у.е.; если размер партии более
20000, то цена 0,039.
Решение. Определим по формуле Уильсона оптимальный размер партии для каждого из трех вариантов.
.
Это
значение не принадлежит промежутку
[1; 10000], значит примем за лучший вариант
случай когда
.
Полученное значение принадлежит промежутку [10001; 19999] и является оптимальным для второго случая
.
Полученное значение принадлежит промежутку [20000; ∞] и является оптимальным для третьего случая
Расчет затрат на управление логистической системой сведем в табл. 3
Таблица 3
Расчет затрат в зависимости от размера заказываемой партии
S |
|
|
|
|
|
5000 |
12500 |
70000 |
82500 |
50000 |
132500 |
8000 |
20000 |
43750 |
63750 |
50000 |
113750 |
10000 |
25000 |
35000 |
60000 |
50000 |
110000 |
10001 |
20002 |
34997 |
54999 |
42000 |
96999 |
13230 |
26460 |
26455 |
52915 |
42000 |
94915 |
19999 |
39998 |
17501 |
57499 |
42000 |
99499 |
20000 |
16000 |
17500 |
33500 |
39000 |
72500 |
20920 |
16736 |
16730 |
33466 |
39000 |
72466 |
25000 |
20000 |
14000 |
34000 |
39000 |
73000 |
Графический вариант решения представлен на рис. 11.
Рис. 11. Определение оптимального размера партии материалов
По графику видно, что самым экономичным вариантом закупки является закупка партией в размере 20920 .
Задача. Определить затраты строительной фирмы на содержание запасов материальных ресурсов на складе за месяц. На июнь требуется 100 тыс.шт. На 1 июля на складе должно быть 10 тыс.шт. Поставки осуществляются по следующему календарному графику: 3 июня – 30 тыс.шт.; 15 июня – 5 тыс.шт.; 20 июня – 40 тыс.шт. Функция затрат определена в зависимости от среднего уровня запаса и выражается в виде f(x) = 4x² – 10x
Р
ешение.
Узнаем потребность в материальных
ресурсах строительной фирмы в день:
Построим график материальных запасов по условию задачи (рис. 12).
Построение графика начнем с конца месяца. На 1 июля, то есть на конец июня на складе должно быть 10 тыс.шт.
За 10 дней до 30 июня была осуществлена поставка. В эти 10 дней фирма израсходовала: 3,3 × 10 = 33 тыс.шт. ресурсов. Значит 20 июня было: 33 + 10 = 43 тыс.шт. ресурсов. 20 июня была осуществлена поставка в 40 тыс.шт. ресурсов. Значит к 20 июня было: 43 – 40 = 3 тыс.шт. ресурсов.
За 5 дней до 20 июня была осуществлена поставка. В эти 5 дней фирма израсходовала: 3,3 × 5 = 16,5 тыс.шт. ресурсов. Значит 15 июня было: 16,5 + 3 = 19,5 тыс.шт. ресурсов. 15 июня была осуществлена поставка в размере 5 тыс.шт. ресурсов. Значит к 15 июня было: 19,5 – 5 = 14,5 тыс.шт. ресурсов.
За 12 дней до 15 июня была осуществлена поставка. В эти 12 дней фирма израсходовала: 3,3 × 12 = 39,6 тыс.шт. ресурсов. Значит 15 июня было: 39,6 + 14,5 = 54,1 тыс.шт. ресурсов. 3 июня была осуществлена поставка в 30 тыс.шт. ресурсов. Значит к 3 июня было: 54,1 – 30 = 24,1 тыс.шт. ресурсов.
За 3 дня до 3 июня была осуществлена поставка. В эти 3 дня фирма израсходовала: 3,3 × 3 = 9,9 тыс.шт. ресурсов. Значит 1 июня было: 9,9 + 24,1 = 34 тыс.шт. ресурсов.
Для
определения затрат нам необходимо
выяснить средний уровень запаса за
месяц. Для этого, используя правило
трапеции рассчитаем средний уровень
запаса между двумя ближайшими поставками
х1, х2, х3, х4
Рис. 12. График материальных запасов
тыс. шт.
тыс. шт.
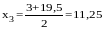
тыс. шт.
тыс. шт.
Рассчитаем средний уровень запаса за месяц Х, как средневзвешенную во времени
Функция затрат определена в зависимости от среднего уровня запаса и выражается в виде f(х)=4х2–10х
Рассчитаем затраты фирмы на содержание запасов материальных ресурсов на складе за месяц:
