1. Расчет линейной электрической цепи постоянного тока

Задание:

1.1 Для заданной схемы определить токи в ветвях с помощью уравнений составленных по законам Кирхгофа.

1.2. Определить ток в ветви с R₁ методом эквивалентного генератора.

1.3. Составить уравнение баланса мощностей.

1.4. Определить показания вольтметра.

1.5. Определить ток I₁ в ветви c сопротивлением R₁ по методу эквивалентного активного двухполюсника и построить график зависимости I₁ = f(R) при изменении R< R₁ < 10R .

1.1 Система уравнений по первому и второму закону Кирхгофа

Зададим направления обхода контуров:

Определяем количество необходимых уравнений по первому и второму законам Кирхгофа:

n = y – 1 = 4 – 1 = 3,

m = n_в – n_j – (y – 1) = 7 – 1 – (4 – 1) = 3,

где y – количество потенциальных узлов,

n_в – число ветвей,

n_j – число ветвей, содержащих источники токов.

Составим уравнения по первому закону Кирхгофа:

a: I₆ – I₂ – I₄ = 0

b: J₄ – I₃ + I₅ = 0

c: I₁ – I₅ – I₆ = 0

Составим уравнения по второму закону Кирхгофа:

I: R₂I₂ – R₄I₄ – R₃I₃ = E₂

II: R₁I₁ + R₃I₃ + R₅I₅ = - E₅

III: R₆I₆ + R₄I₄ – R₅I₅ = E₆ + E₅

Составим матрицу по законам Кирхгофа и найдем токи:

I1	I2	I3	I4	I5	I6
0	-1	0	-1	0	1	0
0	0	-1	1	1	0	0
1	0	0	0	-1	-1	0
0	63	-62	-52	0	0	79
60	0	62	0	24	0	75
0	0	0	52	-24	57	-106

I₁ = 0.66869, A;

I₂ = 0.54439, A;

I₃ = 0.1243, A;

I₄ = -1.00788, A;

I₅ = 1.13217, A;

I₆ = - 0.46348, A;

Расчет цепи методом контурных токов

В

a

ведем контурные токи I₁₁ , I₂₂ , I₃₃ и зададим их направление:

Значения контурных токов найдем из данных выражений:

I₁ = I₂₂

I₂ = I₁₁

I₃ = I₂₂ – I₁₁

I₄ = – I₁₁ – J₃₃

I₅ = I₂₂ – I₃₃

I₆ = I₃₃

Запишем уравнения по методу контурных токов:

I₁₁(R₂ + R₄ + R₃) – I₂₂R₃ – I₃₃R₄ = E₂

– I₁₁R₃ + I₂₂(R₁ + R₃ + R₅) – I₃₃R₂ = – E₅

– I₁₁R₄ – I₂₂R₅ + I₃₃(R₆ + R₄ + R₅) = E₆ + E₅

Составим матрицу и найдем контурные токи:

I11	I22	I33
177	-62	-52	79
-62	146	-24	75
-52	-24	133	-31

После вычислений в программе Gauss мы получили значения:

I₁₁ = 0.54, A;

I₂₂ = 0.66, A;

I₃₃ = – 0.46, A;

Найдем токи:

I₁ = I₂₂ = 0.66, A;

I₂ = I₁₁ = 0.54, A;

I₃ = I₂₂ – I₁₁ = 0.66 – 0.54 = 0.12, A;

I₄ = – I₁₁ – I₃₃ = – 0.54 – 0.46 = -1.00, A;

I₅ = I₂₂ – I₃₃ = 0.66 – (– 0.46) = 1.13, A;

I₆ = I₃₃ = – 0.46, A;

1.2 Определение тока i1 методом эквивалентного генератора

1. Определение U_xx :

Эквивалентная схема замещения:

Составим уравнения по 2 закону Кирхгофа: R₁I₁ + R_ЭГI₁ = E_ЭГ

I₁ =

E_эг = U_xx

a

Составим уравнения по первому и второму закону Кирхгофа:

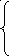I'₁ – I'₂ + I'₃ = 0

I'₁R₄ + I'₂(R₃ + R₂) = –E₂

I'₃(R₆ + R₅) – I'₁R₄ = –E₅ – E₆ Составим матрицу и найдем токи холостого хода:

I'1	I'2	I'3
0	-1	1	0
52	125	0	-79
-52	0	81	106

I'₁ = -0.94299, A;

I'₂ = -0.23972, A;

I'₃ = 0.70327, A;

U_XX = R₅ I'₃ – R₃ I'₁ = 0.70327*24 – (– 0.94299*62) = 75.34386, B;

2. Расчет эквивалентного сопротивления

Последовательность преобразования сопротивлений:

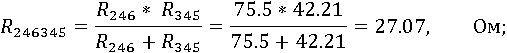
Определим ток I₁ по методу эквивалентного генератора