Лабораторная работа № 4 Вращение плоскости поляризации света при прохождении через кристаллический кварц.

Цель работы: Изучение явления вращения плоскости поляризации световой волны, проходящей через оптически активную прозрачную среду, определение постоянной вращения кристаллического кварца, исследование вращательной способности кварца в зависимости от длины световой волны.

Теоретическое введение.

1. Поляризация световых волн.

Световые волны являются поперечными: колебания напряженностей электрического и магнитного полей происходят поперек направлению распространения волны. Поперечные волны могут находиться в разных состояниях поляризации.

П оляризацию электромагнитных волн обычно определяют по поведению вектора напряженности электрического поля в процессе распространения.

Если вектор непредсказуемо, хаотично меняет направление своих колебаний, свет называется неполяризованным (естественным). Неполяризованный свет излучается большинством тепловых источников (лампы накаливания, Солнце и др.).

Свет, в котором колебания вектора происходят закономерным образом, называется поляризованным.

Состояние поляризации определяют по проекционной картине – по типу траектории конца вектора в проекции на плоскость, перпендикулярную направлению распространения, при наблюдении навстречу волне.

Строго монохроматическая (синусоидальная) волна всегда поляризована. Колебания вектора в ней могут быть представлены в виде суммы взаимно перпендикулярных колебаний:

, где , ;

- единичные векторы вдоль осей и (волна распространяется вдоль оси ). Результат сложения зависит от разности фаз колебаний и соотношения между амплитудами и .

Если колебания происходят в одной плоскости (рис.1б). Такая волна имеет линейную поляризацию (проекционная картина – отрезок прямой линии). Она называется также плоско поляризованной волной.

Если , проекционная картина – окружность (круговая поляризация, правая или левая). На рис.1а показана волна с левой круговой поляризацией. Винтовая линия, изображенная на этом рисунке, представляет собой геометрическое место точек, в которых находится конец вектора в различных плоскостях в фиксированный момент времени. Шаг винтовой линии равен длине волны . С течением времени винтовая линия перемещается вдоль оси . Если «наблюдать» навстречу волне за поведением вектора в фиксированной плоскости, то он вращается против часовой стрелки.

В общем случае строго монохроматическая волна имеет эллиптическую поляризацию (правую или левую).

Оптические устройства, позволяющие из естественного света получить поляризованный свет, называются поляризаторами.

2. Вращение плоскости поляризации при распространении света

в оптически активной среде.

Взаимодействие световой волны с веществом может быть различным в зависимости от её поляризации. Вещества, обладающие способностью вращать плоскость поляризации, называют оптически естественно-активными. Известно, например, что после прохождения плоско поляризованного света через раствор сахара свет остается плоско поляризованным, но плоскость поляризации (плоскость колебаний вектора ) поворачивается на некоторый угол (явление вращения плоскости поляризации). Молекулы сахара имеют левую винтовую структуру. В зависимости от того, является ли световая волна поляризованной по правому или левому кругу, винтообразный характер вращения вектора совпадает с молекулярной винтовой структурой или противоположен ей. Вполне естественно, что в этих двух случаях взаимодействие волн с молекулами будет различным. Поэтому в растворе сахара волны с правой и левой круговой поляризацией будут распространяться с разными фазовыми скоростями: и . В этом случае оказываются разными показатели преломления и и разными коэффициенты поглощения для правой и левой поляризаций.

Пусть падающая волна имеет линейную поляризацию и распространяется вдоль оси . Такую волну можно разложить на две волны с правой и левой круговой поляризацией и одинаковыми амплитудами: . На входе в слой оптически активного вещества (фиксированная плоскость ) вектор вращается по часовой стрелке, а вектор - против часовой стрелки с одинаковой частотой (рис.2а) так, что в плоскости . В любой момент времени сумма векторов и дает вектор , который совершает колебания в плоскости .

З апишем фазовые углы для волн с правой и левой круговой поляризацией в фиксированной плоскости внутри активной среды:

, .

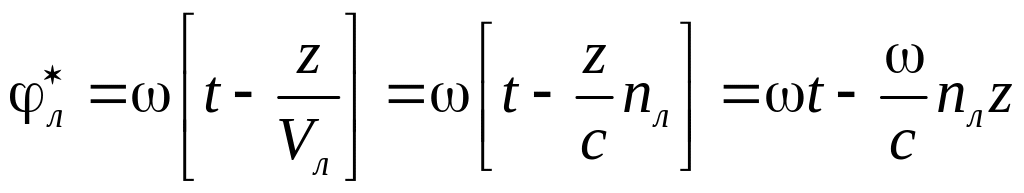Разность фаз равна

Предположим, что , . Так как волна с левой круговой поляризацией распространяется с меньшей скоростью, то до рассматриваемой плоскости она дойдет с отставанием по фазе на величину по сравнению с волной, поляризованной по правому кругу. Вектор повернется в плоскости на угол , который больше, чем угол (рис.2б). Колебания вектора суммарной волны будут происходить в плоскости , которая повернулась вправо на угол относительно плоскости так, что

или

На выходе из слоя толщиной оптически активного вещества плоскость поляризации повернется на угол

,

где - длина волны в вакууме.

Явление вращения плоскости поляризации наблюдается во многих веществах (твердых, жидких, газообразных). Многие оптически активные вещества существуют в виде двух модификаций (разновидностях): одни из них вращают плоскость поляризации линейно поляризованной волны вправо (при наблюдении навстречу волне), для них , , другие вращают влево, для них , .

Жидкие растворы активных веществ содержат асимметричные молекулы с пространственной структурой, не имеющей ни центра симметрии, ни плоскости симметрии. Зеркальное изображение такой молекулы никаким перемещением (поворотом) нельзя совместить с исходной молекулой. Наиболее простая модель такой молекулы – отрезок спирали. Зеркальное изображение левой спирали – правая спираль, никаким поворотом изображение нельзя превратить в левую спираль.

К лассическим примером оптически активного твердого вещества является кристаллический кварц (химическое обозначение ). В природе существуют две модификации кварца, имеющие зеркально-симметричную форму кристаллов (рис.3). Одни из них вращают плоскость поляризации вправо, другие вращают влево. Зеркально-симметричные внешние формы кристаллов на рис.3 обусловлены атомным строением элементарных ячеек кристаллической решетки, состоящей из атомов кремния и кислорода.

Плавленое (аморфное) кварцевое стекло не вращает плоскость поляризации.

Угол , на который поворачивается плоскость поляризации в кварце, вправо или влево в зависимости от модификации, пропорционален длине пути , проходимого в нем света:

,

где - постоянная вращения, которая зависит от длины волны монохроматического света (вращательная дисперсия) и температуры. Для длины пути света в кварце и температуры изменение с изменением иллюстрируется данными в таблице 1. Зависимость от температуры незначительна. Так, например, для нм повышение температуры на 1 K приводит к увеличению на угол .

Таблица 1.

	671	656	589	518	500	486	448	434	405	279	215
	16,6	17,3	21,7	28,6	30,8	32,8	39,2	41,9	48,9	114,5	236