2. Расчет зубчатых колес редуктора

Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками: для шестерни сталь 45, термическая обработка улучшение, твердость НВ230; для колеса – сталь 45, термическая обработка – улучшение, но твердость на 30 единиц ниже – НВ 200.

Допускаемые контакты напряжения определим из формулы (3.9) [1]:

[ ]= ,

где - предел контактной выносливости при базовом числе циклов.

По таблице (Приложение Г) для углеродистых сталей с твердостью поверхностей зубьев менее НВ 350 и термической обработкой (улучшением)

;

- коэффициент долговечности; при числе циклов нагружения больше базового, что имеет место при длительной эксплуатации редуктора, принимают = 1;

- коэффициент безопасности. Примем = 1,10

Для косозубых колес расчетное допускаемое контактное напряжение по формуле (3.10) гл. III (1):

[ ]=0,45 ([ ]+[ ]);

Для шестерни [ ]=

Для колеса [ ]=

Тогда расчетное допускаемое контактное напряжение составит:

[ ]=0,45(482+428)=410 МПа

Требуемое условие [ ]≤1,23[ ] выполнено.

Коэффициент К_Нβ, несмотря на симметричное расположение колес, относительно опор (рисунок 2), примем выше рекомендуемого для этого случая, так как со стороны цепной передачи действуют силы, вызывающие дополнительную деформацию ведомого вала и ухудшают контакт зубьев.

Принимаем предварительно как в случае несимметричного расположения колес, значение К_Нβ=1,25

Принимаем для косозубых колес коэффициент ширины венцы по межосевому расстоянию предпочтительно выбирать:

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев по формуле (3.7) [1]:

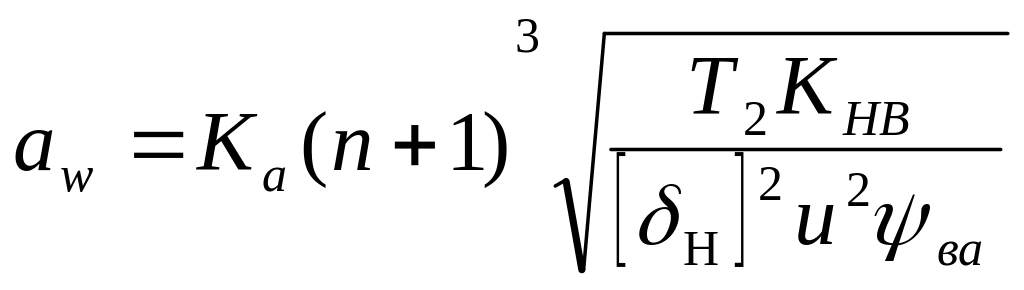
где К_а - для косозубых колес К_а = 43,

u -передаточное число нашего редуктора:

u = u_р = 5

Полученное межосевое расстояние округляем до ближайшего значения межосевого расстояния по ГОСТ 2185-66 а_w=160 мм (Приложение Д).

Нормальный модуль зацепления принимаем по следующей рекомендации:

Принимаем по ГОСТ 9563-60* m_n=2 мм (Приложение Е)

Зададим предварительно угол наклона зубьев β=10º и определим число зубьев шестерни и колеса по формуле (3.16) [1]:

_,

Принимаем z₁ = 26; тогда z₂ = z₁ · u = 26 · 5 = 130.

Уточненное значение угла наклона зубьев:

что соответствует углу ß=12º50´.

Определим основные размеры шестерни и колеса:

Диаметры делительные находим из формулы (9):

₍₉₎

Проверка:

Диаметры вершин зубьев определим по формуле (10):

₍₁₀₎

Ширина колеса определяется из формулы (11):

₍₁₁₎

Ширина шестерни составит:

Определяем коэффициент ширины шестерни по диаметру:

Окружная скорость колес и степень точности передачи составит:

Для косозубых колес при скорости v до 10 м/с следует принять 8-ю степень точности.

Коэффициент нагрузки составит:

Значение даны в (Приложение Ж)

При =1,274, твердости НВ ≤ 350 и несимметричном расположении колес относительно опор с учетом изгиба ведомого вала от натяжения цепной передачи ≈1,155.

По таблице 3.4 гл. III [1] при скорости V = 2,03 м/с и 8-й ступени точности ≈1,08.

По таблице (Приложение И) для косозубых колес при V ≤ 5 м/с имеем =1,0. Таким образом,

=1,155 · 1,08 · 1,0 = 1,245

Проверка контактных напряжений по формуле (3.6) [1]:

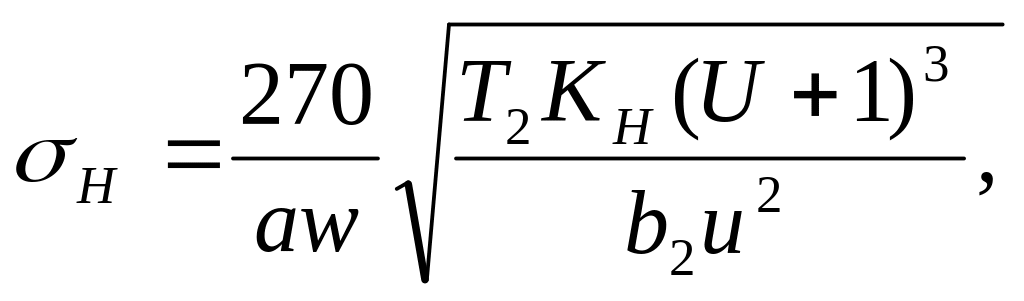
Силы, действующие в зацеплении: окружная, радиальная и осевая.

Окружная сила определяется по формуле (8.3) [1]:

Радиальная определяется по формуле (8.4) [1]:

Осевая по формуле (8.5) [1]:

Проверяем зубья на выносливость по напряжениям изгиба по формуле (3.25) [1]:

где K_F - коэффициент нагрузки

Коэффициент нагрузки определяется по формуле (3.26) [1]:

K_F = K_FB K_FV

где K_FB – коэффициент концентрации нагрузки;

K_FV - коэффициент динамичности нагрузки

По таблице 3.7[1] при = 1,274, твердости НВ ≤ 350 и несимметричном расположении зубчатых колес относительно опор K_Fβ =1,33.

По таблице 3.8 [1] K_FV = 1,3.

Таким образом, коэффициент составляет:

K_F = 1,33 · 1,3 = 1,73

Y_F – коэффициент, учитывающий форму зубы и зависящий от эквивалентного числа зубьев z_v [см. гл. III, с пояснением к формуле (3.25) [1]:

у шестерни

у колеса

Y_F1 = 3,84 и Y_F2 = 3,60 ( стр. 42) [1]

Допускаемое напряжение по формуле (3.24) [1]:

По таблице 3. [1] для стали 45 улучшенной при твердости НВ ≤ 350, =1,8НВ.

Для шестерни

=1,8 · 230 = 415 МПа

Для колеса = 1,8 · 200 = 360 МПа

Определим коэффициент безопасности по формуле (3.27) [1]:

_,

где =1,75 ( таблица 3.9) [1];

=1 (для поковок и штамповок)

Следовательно =1,75

Допускаемые напряжения составят:

Для шестерни

Для колеса

Находим отношение

Для шестерни

Для колеса

Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше.

Определяем коэффициенты Y_B и K_Fα по формуле (3.25) [1]:

Для средних значений коэффициента торцового перекрытия ε_α = 1,5 и 8-й ступени точности =0,92.

Проверяем прочность зуба колеса по формуле (3.27) [1]:

Так как условие прочности выполнено.