Пример 2.1.

Пусть мы внесли в банк 100$ под 10% годовых.

Через год сумма нашего вклада FV₁ составит:

FV_1год=100+0,10100=110$

Если мы не будем изымать средства из банка, то после второго года эта сумма FV₂ составит:

FV_2год=100+0,10100+100+0,10 1000,10= =100(1+0,10)+100(1+0,10)0,10 = 100(1+0,10)1+0,10 = 100(1+0,10)²=100(1,10)²=

и т.д.

FV_nгод=PV(1+r)ⁿ (2.1)

где: FV_{n год} – будущая стоимость через n лет;

PV – present value – настоящая стоимость в данный момент (текущая

стоимость).

r – норма доходности, прибыльности от вложения; процентная ставка

для периодов n; ставка дисконта; ставка сравнения

Для определения множителя (1+r)ⁿ

^{можно воспользоваться таблицами (Приложение 1.)}

^{Формула (2.2)}

PV= FV_n _ = FV_n  ___1___

(1+r)ⁿ (1+r)ⁿ

Пример 2.2.

После некоторых мероприятий фирма планирует получать экономию (доход) $1000 в год. Сэкономленные деньги предполагается разместить на депозите под 5% годовых с тем, чтобы через 5 лет накопленные деньги использовать для инвестирования. Какая сумма окажется на банковском счете фирмы? (При прочих равных условиях). r=0,05 n=5.

Решение представим на рисунке 2.3.

0

1

2

3

4

5

годы

1000 1000 1000 1000 1000

1000

1050

1103

1158

1216

_________

 5527

Рис. 2.3. Схема вычисления будущей стоимости денег

1. после 4-го года генерируемая сумма в $1000 в конце 5-го года превратится в $1050, а именно:

1000+(0,051000)=1000 (1+0,05)¹=10001,05¹=1050.

Аналогично рассуждая, определим будущую стоимость для последующих периодов.

2. 1000(1,05)²=10001,1025=1102,5

3. 10001,05³=1158

4. 10001,05⁴=1216

Следовательно, в сумме на депозите через 5 лет будет $5527.

Этот пример характеризует аннуитет – равномерный поток по $1000 ежегодно. Его можно рассчитать, используя таблицу аннуитета будущей стоимости (Приложение2). r =5%; n - 5 лет; коэффициент аннуитета будущей стоимости равен 5,527.

Для определения суммарной будущей стоимости денег FV =10005,527.

Рассмотрим пример с неодинаковыми элементами денежного потока.

Пример2.3.

Пусть проект генерирует следующие Cash flow:

CF₁=100 CF₅=200

CF₂=200 CF₆=0

CF₃=200 CF₇=1000

CF₄=200

Необходимо определить текущие, настоящие значения стоимости денег PV(т.е. оценка денег на «сегодня»); r=0,06; n=7 лет.

Решение также представим на рисунке 2.4. (решим обратную задачу). Воспользуемся значениями коэффициентов дисконтирования (Приложение3).

_{0 1 2 3 4 5 6 7 годы}

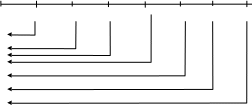
100 200 200 200 200 0 1000

94,34

178,00

167,92

158,42

149,46

0

665,10

_______

 1413,24

Рис 2.4. Схема вычисления текущей стоимости денег

У инвестора всегда есть альтернатива более выгодного вложения капитала. Рассмотрим пример, характеризующий возможность выбора при двух вариантах вложения капитала.