3.2 Синтез несущего механизма

Несущий механизм связан с рабочим органом и должен обеспечивать ему возвратно поступательное движение с высоким показателем коэффициента производительности:

=

Дано: k=1,38; ν_max=24⁰; а=0,015м; υ_ср=3.07м/с

1.Определим угол перекрытия :

Вычислим угол -соответствующий холостому ходу :

, тогда =

Теперь определим -угол поворота главного вала ,соответствующий рабочему ходу рабочего органа :

2.Находим размеры звеньев по следующим формулам:

Из прямоугольного треугольника OBA: r=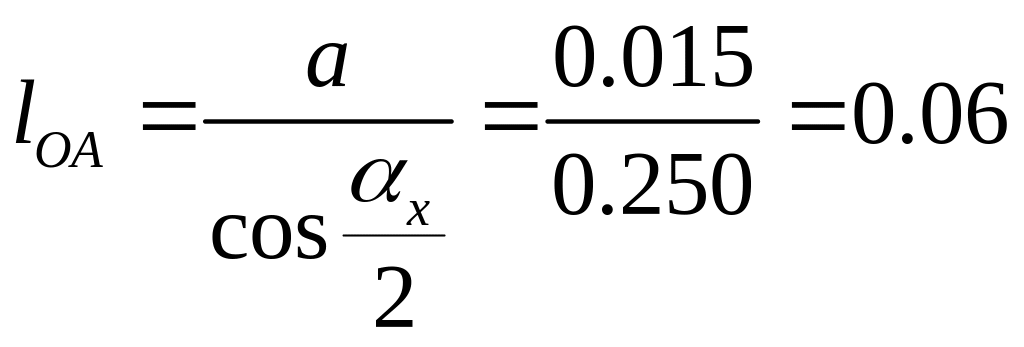 м

Длина кулисы ВС: м; Диаметр поршня: d_П=1.5r=0.09м;

Из треугольника СВD найдём

3.3Синтез кулачкового механизма

Кулачковым называется механизм с высшей кинематической парой, входное звено которого (обычно) называется кулачком, а выходное – толкателем. Он предназначен для преобразования вращательного или поступательного движения кулачка в возвратно-поступательное или во возвратно- вращательное движение толкателя.

Кулачковые механизмы подразделяются по следующим признакам:

1. По расположению звеньев в пространстве (пространственные и плоские).

2. По виду движения кулачка (вращательное, поступательное, винтовое).

3. По виду движения выходного звена (возвратно-поступательное (толкатель); возвратно-вращательное (коромысло))

4. По виду кулачка (дисковый, цилиндрический, коноид (сложный пространственный)).

5. По форме рабочей поверхности выходного звена (плоское, цилиндрическое, сферическое, заострённое, эвольвентное).

6. По способу замыкания ВКП (силовое, геометрическое).

Задача синтеза кулачковых механизмов заключается в определении основных размеров и профиля кулачка по заданным кинематическим и динамическим параметрам.

В нашем случае угол возвращения φ_возв=72⁰; угол удаления φ_уд=90⁰. Эти углы разделены между собой фазовым углом дальнего стояния φ_д.с.=18.⁰

Угол дальнего стояния – угол поворота кулачка, при котором толкатель в крайнем верхнем положении совершает выстой.

Угол возвращения – угол поворота кулачка, при котором толкатель движется из крайнего верхнего положения в крайнее нижнее.

Угол ближнего стояния – угол, при котором толкатель в крайнем нижнем положении совершает выстой.

Выбираем закон движения толкателя кулачкового механизма на фазах удаления и возвращения.

На фазе удаления закон движения Параболический:

при 0≤φ≤φ_{1; при φ1}≤φ≤φ_у

График изменения перемещения толкателя

при 0≤φ≤φ_1; при φ₁ ≤φ≤φ_уд

График аналога скорости толкателя

при 0≤φ≤φ_1; при φ₁≤φ≤φ_уд

График изменения аналога ускорения толкателя

На фазе возвращения модифицированный линейный закон движения:

при 0≤φ≤φ_{1 ;} при φ₁≤φ≤ (φ_возв-φ₁₎

при (φ_возв-φ₁₎ ≤φ≤ φ_возв

График изменения перемещения толкателя

при 0≤φ≤φ_1; при φ₁≤φ≤(φ_возв-φ_1);

(φ_возв-φ₁₎≤φ≤φ_возв;

График аналога скорости толкателя

при 0≤φ≤φ_1; 0 при φ₁≤φ≤(φ_возв-φ_1); при(φ_возв-φ₁₎ ≤φ≤ φ_возв

График изменения аналога ускорения толкателя

Результаты расчётов заносим в таблицу 2:

Фаза	i	k	,0				,0	,0	Ri,мм
Удаление	0	0	0	0	0	0	-30	0	59
	1	9	9	0.3876	7.295	89.807	-23.331	8.997	59.336
	2	18	18	2.9181	26.394	145.31	-3.291	17.976	61.545
	3	27	27	8.9181	50.001	145.31	18.86	26.933	66.873
	4	36	36	18.387	69.099	89.807	29.679	35.878	75.486
	5	45	45	30	76.394	0	30	44.825	86.295
	6	54	54	41.613	69.099	-89.807	23.129	53.784	97.289
	7	63	63	51.082	50.001	-145.31	11.345	62.757	106.351
	8	72	72	57.082	26.394	-145.31	-1.645	71.743	112.128
	9	81	81	59.613	7.295	-89.807	-11.341	80.737	114.572
	10	90	90	60	0	0	-14.871	89.736	114.946
Возвращение	11	0	108	60	0	227.97	---------	107.736	114.946
	12	12	120	55.556	39.789	151.98	---------	119.746	110.657
	13	24	132	44.444	63.662	75.991	---------	131.776	99.991
	14	36	144	30	71.62	0	---------	143.728	86.295
	15	48	156	15.556	63.662	-75.991	---------	155.893	72.889
	16	60	168	4.444	39.789	-151.98	---------	167.965	62.888
	17	72	180	0	0	-227.97	---------	180	59

Определим основные размеры и е кулачкового механизма по условию ограничения угла давления только на фазе удаления, так как высшая пара имеет силовое замыкание и кулачок вращается против часовой стрелки. В этом случае воспользуемся следующими формулами:

Для равноубывающего удаления толкателя угол, при котором имеет наибольшее значение, , а аналог скорости и перемещение , соответствующие этому углу,

Подставив эти значения в формулы, получаем:

Принимаем ; При вращении кулачка против часовой стрелки положительному значению смещения е соответствует расположение линии движения справа от центра вращения кулачка.

Определяем по формуле угол давления только на фазе удаления , так как высшая пара имеет силовое замыкание и заклинивание механизма может произойти только на фазе удаления (на фазе возвращения толкатель движется под действием пружины).

Так как ,то значения и е удовлетворяют условию синтеза.

Определяем полярные координаты центрового профиля кулачка по формулам:

где на фазе удаления , а на фазе удаления , к изменяется от 0 до10.

Результаты расчетов заносим в таблицу 2. По полученным значениям и строим центровой профиль кулачка. Для этого в масштабе проводим ок-

ружности радиусами: ; Касательно к окружности радиусом е слева проводим линию движения толкателя уу. Соединив точку пересечения направляющей уу с окружностью радиусом (точку ) с центром вращения кулачка (точка ), получим радиус-вектор , соответствующий началу удаления. От этого радиуса в направлении, противоположном вращения кулачка, отложим полярные углы , на сторонах, которых строим в масштабе радиусы-векторы .

Соединив плавной кривой концы радиус-векторов, получим центровой профиль кулачка.

На фазе дальнего стояния кулачек очерчивается дугой радиусом

На фазе возвращения построение аналогично построению на фазе удаления.

На фазе ближнего стояния профиль очерчивается радиусом

Определим минимальный радиус кривизны центрового профиля кулачка как радиус вписанной окружности выпуклого участка профиля кулачка, где кривизна его окажется наибольшей. На этом участке произвольно выбираем три точки , и и соединяем их двумя хордами. В середине хорд восстанавливаем к ним перпендикуляры, точку пересечения которых М принимаем за центр вписанной окружности.

Действительный профиль кулачка найдем как эквидистантную кривую, отстоящую от центрового профиля на расстоянии, равном радиусу ролика.

Окончательно выбираем

Для получения действительного профиля кулачка на его центровом профиле выбирается ряд точек , из которых проводим полуокружности (в сторону уменьшения радиуса-вектора кулачка) радиусом ролика . Огибающая этих полуокружностей и является действительным профилем кулачка.

Рассчитаем характеристики замыкающей пружины. Для определения силы пружины и ее жесткости построим график сил инерции толкателя в функции перемещения (Рис.9).

Для расчета выбираем фазу удаления, так как на этой фазе аналог ускорения толкателя имеет наибольшее значение , чем на фазе возвращения. Для закона с равноубывающим удалением толкателя:

Сила инерции толкателя:

где =5h=300г,

а угловая скорость кулачка: ,

где

Принимаем минимальную реакцию а предварительное напряжения пружины . Выбрав масштабные коэффициенты и , производим построение рис. Соединив точки a и b, получим зависимость . Максимальная сила пружины . Жесткость пружины: