12

Лабораторная работа № 1

ИССЛЕДОВАНИЕ МЕТОДОВ ФОРМИРОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН ДЛЯ МОДЕЛИРОВАНИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

1.1. Моделирование случайных процессов. Случайные числа

При исследовании сложных технологических систем методом имитационного моделирования существенное внимание уделяется учету случай­ных факторов.

В качестве математических схем, используемых для форма­лизации действия этих факторов, используются случайные со­бытия, случайные величины и случайные процессы (функции).

Формирование на ЭВМ реализаций случайных объектов любой природы сводится к выработке и преобразованию случайных чисел.

Количество случайных чисел, используемых для формиро­вания одной реализации моделируемого процесса, колеблется в достаточно широких пределах. Оно исчисляется в простейших случаях десятками тысяч, но нередко может достигать миллио­нов чисел и более.

При исследовании систем методом имитационного модели­рования существенное количество операций расходуется на дей­ствия со случайными числами. Поэтому не будет преувеличе­нием сказать, что наличие простых и экономных способов фор­мирования последовательности случайных чисел во многом определяет возможность практического использования этого метода.

Обычно считают, что этим требованиям удовлетворяет со­вокупность случайных чисел с равномерным распределением в интервале (0, 1).

В дальнейшем будет показано, что с помощью равномерно распределенных случайных чисел можно конструировать как случайные события, возникающие с любой заданной вероят­ностью, так и случайные величины, обладающие практически любым законом распределения.

1.2. Свойства равномерного распределения.

Непрерывная случайная величина имеет равномерное распре­деление в интервале (рис. 1.1а), если ее функция плотности равна

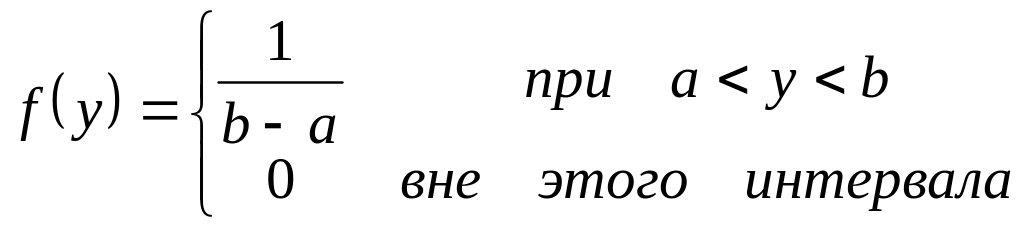
Функция распределения случайной величины имеет вид

.

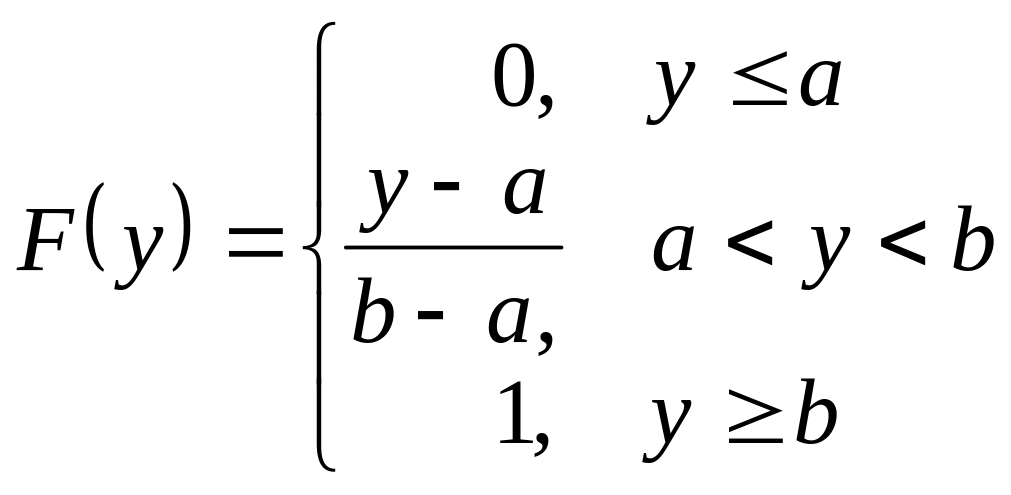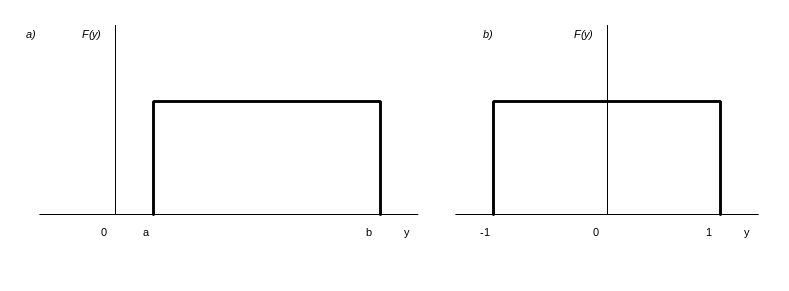
Рис.1.1. Плотности распределения вероятностей:

а) общий случай; б) центрированная случайная величина в диапазоне (-1,+1)

Математическое ожидание М [ ] и среднее квадратическое отклонение соответственно равны

В частном случае равномерного распределения в интервале (0, 1) случайная величина имеет функцию плотности

,

функцию распределения

,

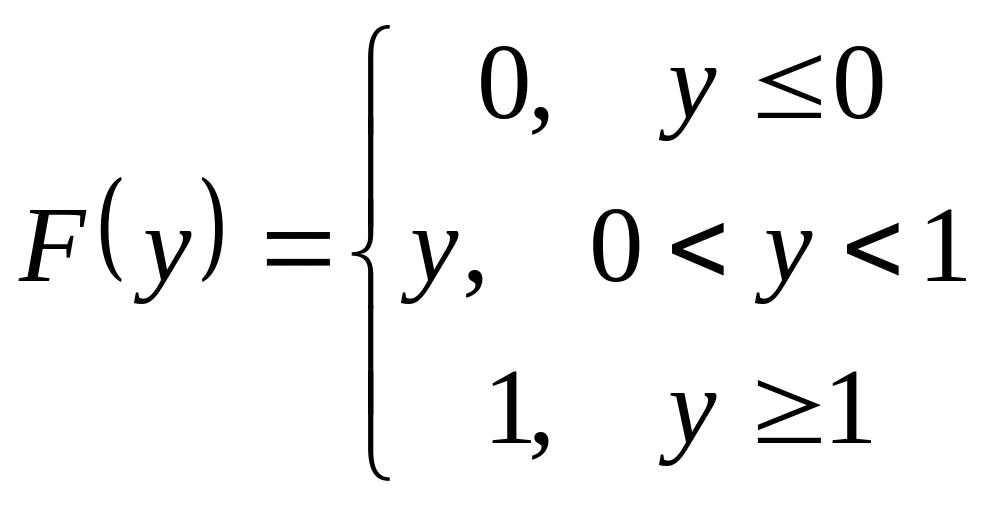а математическое ожидание и среднее квадратическое отклоне­ние соответственно равны

.

Данная случайная величина часто используется для реализации датчиков случайных чисел. В МS Ехсеl такой датчик выполнен в виде функции СЛЧИС, которая при обращении к ней выдает случайные числа в интервале (0, 1).

При моделировании случайных чисел удобно использовать центрированную случайную величину с равномерным законом распределения в диапазоне (-1,+1) (рис.1.1б) , с помощью которой можно легко моделировать случайные числа с математическим ожиданием в диапазоне (а, b)

. (1.1)

Пример моделирования случайных чисел с равномерным законом распределения приведен в Задании 1.1.

1.3. Формирование возможных значений случайных величин с

заданным законом распределения

Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом слу­жат случайные величины, имеющие равномерное распределение в интервале (0, 1). Другими словами, возможные значения случайной величины, имеющей равномерное распределение в интервале (0, 1), могут быть преобразованы в возможные значения случайной величины , закон распределения которой задан.

Существуют два основных пути такого преобразования слу­чайных чисел.

1. Один из них, который может быть назван пря­мым, состоит в реализации некоторой операции над числом формирующей число , имеющее (точно или приближенно) за­данный закон распределения.

2. Другой основывается на модели­ровании условий соответствующей предельной теоремы теории вероятностей.