§1.3. Вертикалы и альмукантараты. Меридианы и параллели

Большой круг небесной сферы, плоскость которого проходит через отвесную линию и перпендикулярна плоскости истинного горизонта, называется вертикалом.

Вертикал, проходящий через точки востока E и запада W, называется первым вертикалом, причём та его половина, которая проходит через точку E называется восточной частью первого вертикала, а другая проходящая через точку W – западной частью первого вертикала (рис. 1.3).

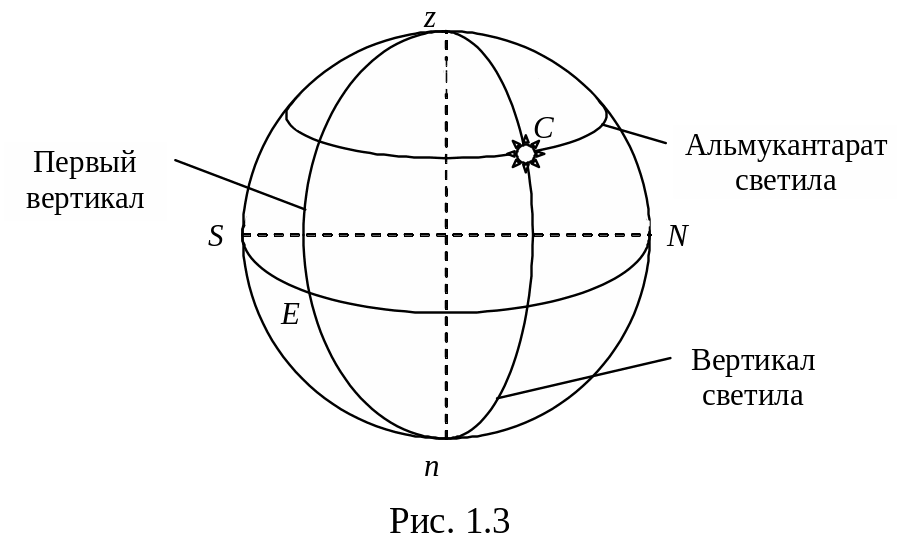
Вертикал, проходящий через центр светила С называется вертикалом светила, при этом под этим термином пониматся лишь только та его половина, от зенита z до надира n, на которой непосредственно расположено светило.

Малые круги небесной сферы, параллельные истинному горизонту (перпендикулярные отвесной линии) называются альмукантаратами. Альмукантарат, проходящий через центр светила С на небесной сфере называется альмукантаратом светила.

Большой круг небесной сферы, плоскость которого проходит через ось мира P_NP_S и перпендикулярна плоскости небесного экватора, называется меридианом (рис. 1.4).

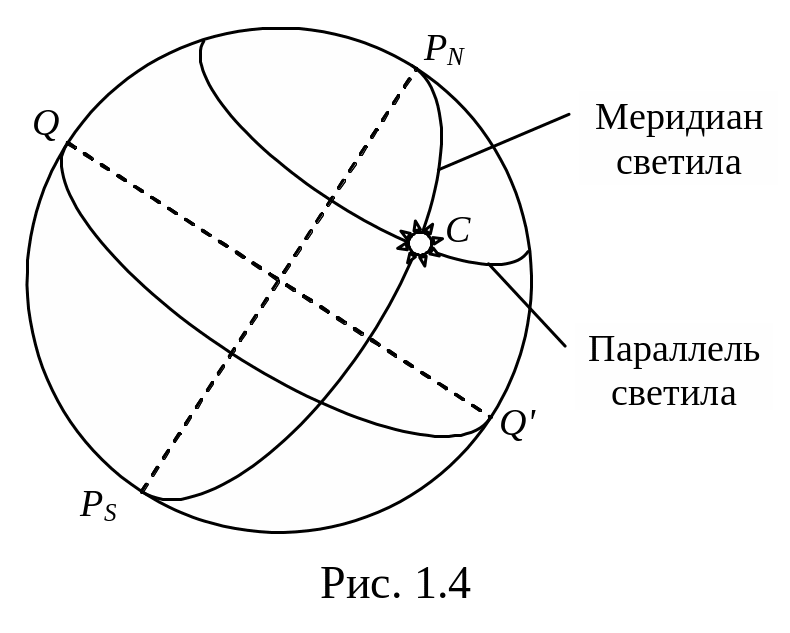
Меридиан, проходящий через центр светила С называется меридианом светила, при этом меридианом светила считается та половина, от северного P_N до южного полюса P_S, на которой непосредственно располагается светило.

Малые круги параллельные плоскости небесного экватора (перпендикулярные оси мира) называются параллелями. Параллель, проходящая через центр светила С называется параллелью светила.

§1.4. Системы сферических координат

Для определения места положения точки на плоскости необходимо и достаточно знать две координаты. Так, для определения места положения какого-либо объекта на поверхности Земли должны быть известными его широта и долгота.

Для определения положения светила на небесной сфере пользуются сферическими системами координат. Они представляют собой дуги взаимно перпендикулярных больших кругов, расположенных определённым образом на поверхности сферы относительно заранее выбранных плоскостей, принятых за основные для отсчёта координат. Такими плоскостями являются:

• истинный горизонт;

• небесный экватор;

• меридиан наблюдателя.

Горизонтная система координат

Основным направлением в горизонтной системе координат является отвесная линия. Основными плоскостями – истинный горизонт и меридиан наблюдателя. Координатами являются, высота светила h и азимут А.

Высотой светила h называется дуга вертикала светила от истинного горизонта до места светила, считаемая от 0 до 90 (рис. 1.5). При этом светила расположенные над горизонтом имеют положительную высоту, а под горизонтом – отрицательную. Например, светило С изображенное на рис. 1.5 имеет высоту h = 50.

У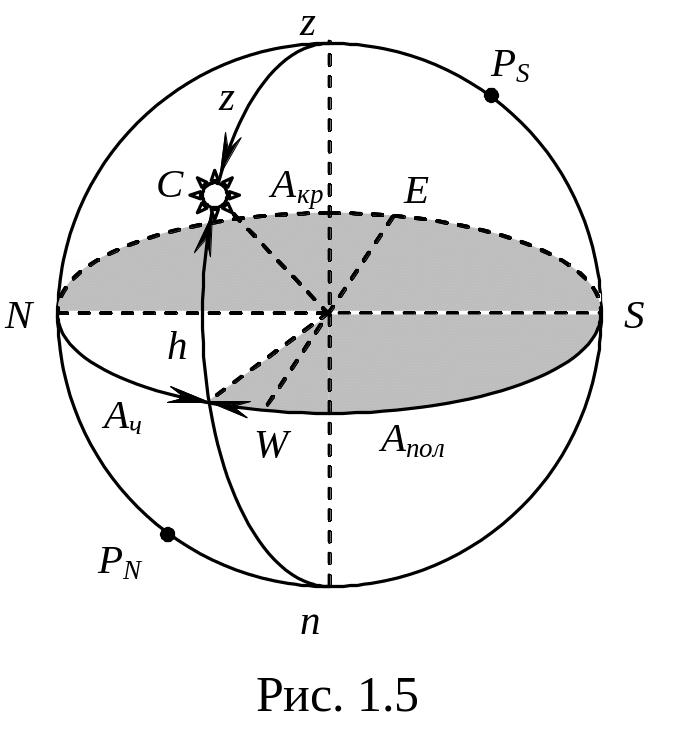 гол при центре сферы, на который опирается дуга h, также называется высотой светила.

В горизонтной системе координат используется ещё одна координата под названием зенитное расстояние z. Зенитным расстоянием z называется дуга вертикала светила от точки зенита до места светила считаемая от 0 до 180. Зенитным расстоянием также называется угол при центре сферы, на который опирается дуга z.

Исходя из определения высоты светила h и зенитного расстояния z, а также рис. 1.5, можно получить следующее очевидное равенство

,

таким образом, зенитное расстояние является дополнением высоты светила до 90.

Азимутом А называется дуга истинного горизонта заключенная между меридианом наблюдателя и вертикалом светила.

Угол при центре сферы на который опирается дуга А, также называется азимутом.

Так как точка зенита z является полюсом истинного горизонта, то азимут светила можно измерять сферическим углом¹ при зените, который образуется дугой между меридианом наблюдателя и вертикалом светила.

Азимут имеет три счета:

• круговой А_кр;

• полукруговой А_пол;

• четвертной А_ч.

Круговым азимутом А_кр называется дуга истинного горизонта от точки севера N в сторону востока Е до вертикала светила считаемая от 0 до 360. Например, для светила С на рис. 5 круговой азимут запишется следующим образом А_кр = 285.

Полукруговым азимутом А_пол называется дуга истинного горизонта от полуночной части меридиана наблюдателя в сторону востока Е или запада W считаемая от 0 до 180. Например, для светила С на рис. 1.5 полукруговой азимут запишется следующим образом А_пол = S105W или А_пол = 105SW.

Четвертным азимутом А_ч называется дуга истинного горизонта от точки севера N или юга S в сторону востока Е или запада W от 0 до 90. Например, для светила С на рис. 1.5 четвертной азимут запишется следующим образом А_ч = N75W или А_ч = 75NW.

Преимуществом горизонтной системы является её наглядность, а также наличие приборов для измерения координат: пеленгатор компаса для измерения азимутов и секстан для измерения высот светил. Недостатком этой системы координат является постоянное изменение координат вследствие суточного вращения Земли.