Лабы / седьмая

Министерство образования и науки Российской Федерации

Федеральное автономное государственное образовательное учреждение высшего образования

«Национальный исследовательский Томский политехнический университет»

Инженерная школа электроэнергетики

Отделение электроэнергетики и электротехники

Лабораторная работа №7

«МОДЕЛИРОВАНИЕ АСИНХРОННОГО ДВИГАТЕЛЯ»

Вариант №5

Выполнил:

Студент группы 5А6Б _____________

(подпись)

Проверил:

Преподаватель _____________ Бай Ю. Д.

(подпись)

_____________

(дата)

Томск 2019

Цель работы: Создание математической модели асинхронного двигателя в установившемся режиме работы в среде MathCAD.

Теоретические сведения

Свойства нагрузки оказывают непосредственное влияние на устойчивость параллельной работы станций. Однако характеристики нагрузки существенны не только с этой точки зрения. В определенных условиях нагрузка сама может оказаться неустойчивой. Так, например, известно, что у асинхронных двигателей при значительном снижении напряжения, когда тормозной момент превышает вращающий момент, на их выводах происходит «опрокидывание», и они останавливаются.

На рис. 1.1 приведена схема замещения асинхронного двигателя, при построении которой не учитывались потери активной мощности в стали, а также в меди статора. Эта схема часто упрощается и приводится к виду, изображенному на рис. 1.2, где индуктивное сопротивление цепи намагничивающего тока отнесено непосредственно к выводам двигателя.

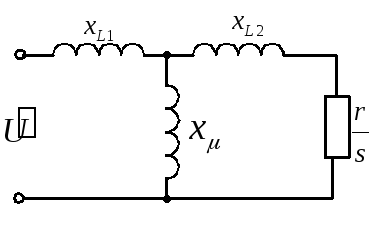
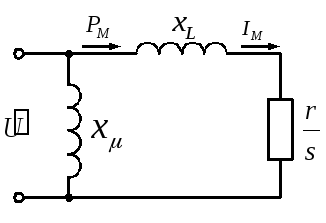
Рис. 1.1 Рис. 1.2

Сопротивление х_L в схеме рис. 1.2 представляет собой сумму индуктивных сопротивлений рассеяния статора и ротора

х_L = х_L1 + х_L2 .

Активная мощность Р_М в схеме рис. 7.2 представляет собой мощность, получаемую двигателем из сети, которая определяется, как произведение вращающего момента М_вр на угловую скорость вращения магнитного потока двигателя ω

.

Угловая скорость вращения магнитного потока двигателя при неизменной частоте сети остается постоянной при любом скольжении двигателя, и, следовательно, вращающий момент двигателя М_вр пропорционален мощности Р_М, а в относительных единицах может быть принят численно ей равным.

На рис. 1.1 показана характеристика установившегося режима работы двигателя 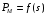и характеристика тормозного момента , преодолеваемого двигателем, т.е. момента сопротивления со стороны приводимого двигателем механизма. В общем случае характеристика тормозного момента имеет падающий характер, однако в расчетах эту характеристику часто считают горизонтальной и полагают Р_Т(s) = const.

Рис. 1.3

Как видно, установившийся режим работы двигателя возможен при двух точках пересечения характеристики момента двигателя и тормозного момента. Однако лишь одна из них определяет устойчивый и, следовательно, реально осуществимый режим.

Задание

Расчет ведется в относительных единицах (для упрощения индексы * опускаются). Примем U_ном = 1.

Для схемы рис. 1.2

1. Вывести зависимости активной и реактивной мощностей от скольжения 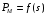, и построить в среде MathCAD при

U = 1; U = 0,9: U = 0,7; U = 0,5.

2. При выбранном согласно варианту (таблица 1.1) тормозном моменте Р_Т по зависимостям п.1 определить скольжение, соответствующее установившемуся режиму двигателя, а также напряжение, при котором произойдет «опрокидывание» двигателя.

3. Определить при U = 1 максимальную мощность двигателя Р_Мmax и критическое скольжение s_кр, при котором она достигается (так называемый опрокидывающий момент) аналитически и по зависимостям п.1.

4. Определить математический критерий статической устойчивости двигателя.

Исходные данные

Таблица 1.1 – Исходные данные

x, о.е.	r, о.е.	о.е.
5,8	1	0,04

Решение

1. Выразим по закону Ома ток I_М в схеме рис. 1.2 (в комплексной форме), считая известными напряжение и сопротивления и определим модуль тока:

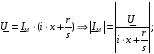
Подставим полученное выражение в закон Джоуля-Ленца для активной и реактивной мощностей:

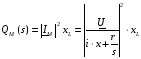
Строим полученные зависимости в среде MathCAD при указанных значениях напряжения на входе двигателя.

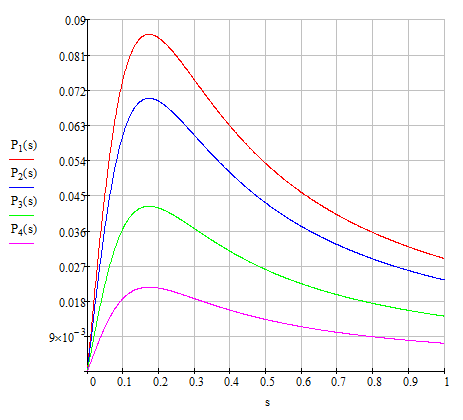
Рис. 2. Зависимости активной мощности от скольжения

Рис. 3. Зависимости реактивной мощности от скольжения

2. Построим на графике 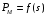характеристику тормозного момента Р_Т (s) = const. По точке пересечения данной прямой с зависимостью 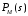при U = 1 найдем скольжение двигателя в нормальном рабочем режиме.

Рис. 4. Зависимости активной мощности от скольжения

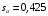
При значительных снижениях напряжения (на 30% и более) зависимость 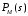проходит ниже или касается зависимости Р_Т (s). В результате происходит нарушение устойчивой работы двигателя, двигатель затормаживается, резко возрастает потребляемый ток и реактивная мощность. Таким образом, опрокидывание двигателя происходит при напряжении, когда тормозной момент будет больше или равен максимальному вращающему моменту.

3. Максимум активной мощности двигателя найдем, определяя производную по скольжению и приравнивая ее к нулю

.

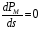Отсюда выражается критическое скольжение s_кр, и при этом значении определяется Р_Мmax

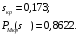
4. Критерием статической устойчивости двигателя является положительный знак избыточного момента ΔР = ΔР_М – ΔР_Т.

ΔР = ΔР_М – ΔР_Т=0,08622-0,04=0,822.

Построим в среде MathCAD зависимость производной 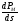от скольжения s. Такое построение производится автоматически, без вывода формулы.

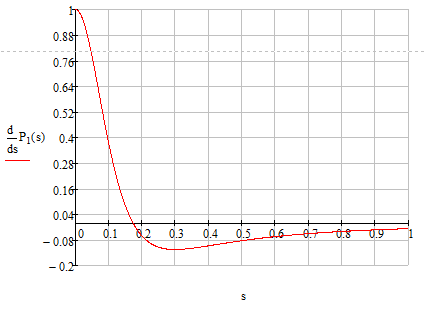Рис. 5. Зависимости от скольжения

С помощью полученного графика определим s_кр и сравним с s_кр, полученным в п.3.

Вывод: В данной лабораторной работы была рассмотрена математическая модель асинхронного двигателя в установившемся режиме работы. Получены зависимости активной и реактивной мощностей и производной активной мощности от скольжения. По данным зависимостям определена максимальную мощность двигателя Р_Мmax и критическое скольжение s_кр, при котором она достигается. Так же s_кр определено аналитически, оно практически совпадает со значением, найденным по графику.

Критерий статической устойчивости выполняется, так как знак избыточного момента является положительным.