Лабы / EMPP_laba_1

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Направление 13.03.02 – Электроэнергетика и электротехника

Инженерная школа энергетики

Лабораторная работа №1

«Исследование статической устойчивости одномашинной системы»

по дисциплине «Математическое моделирование электроэнергетических систем»

Вариант 262

Выполнили студент гр. 5А6Б _______ _____ Кошкин Д.Р.

^{Подпись Дата}

Проверил преподаватель _______ _______ Исаев Ю.Н.

^{Подпись Дата}

Томск 2019

Цель работы: Изучить влияние параметров внешней электрической сети и промежуточной нагрузки на статическую устойчивость одномашинной энергосистемы.

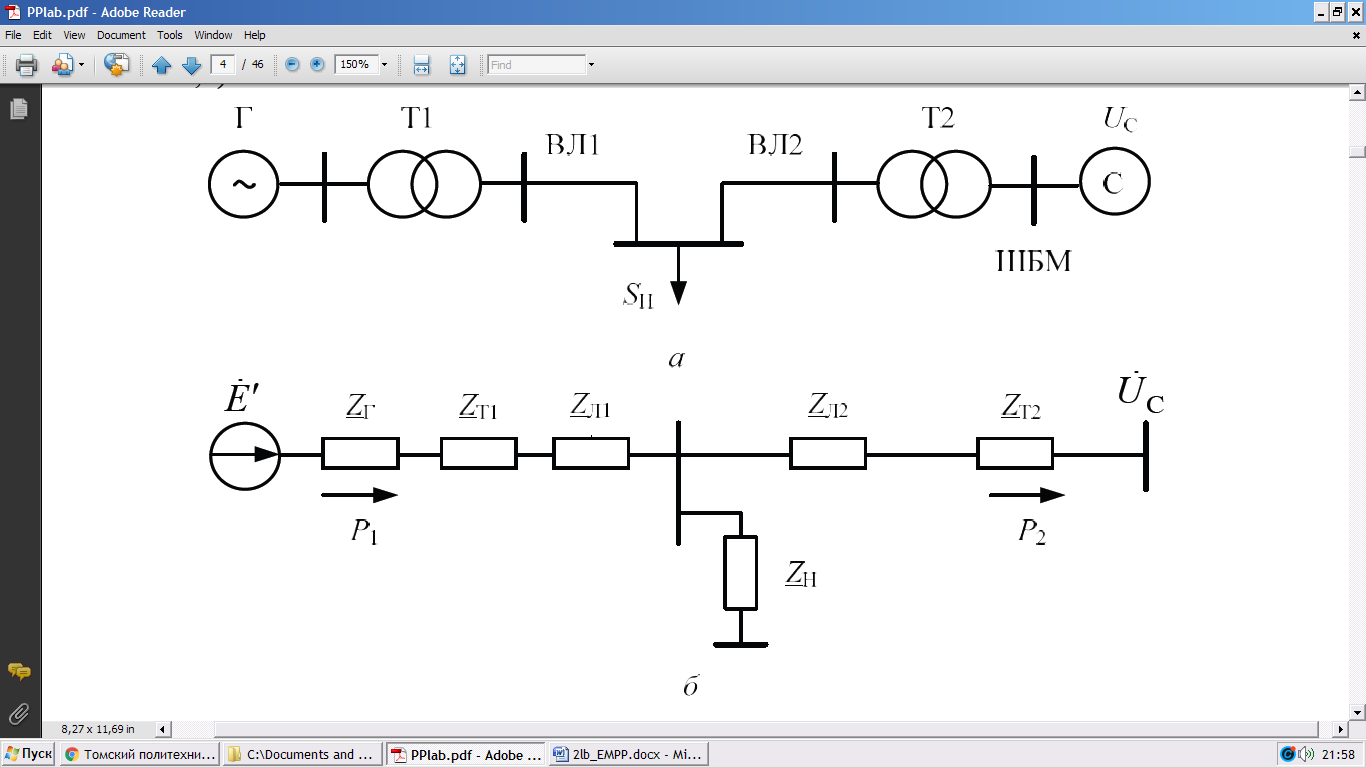
Рисунок 1 – Электрическая схема (а) и схема замещения (б) одномашинной энергосистемы

Исходные данные

Исходные данные для выполнения работы согласно варианту представлены в таблице 1.

Таблица 1 - Исходные данные

Вариант	Мощность реактора, Qp, МВАр	Мощность конденсаторной батареи, Qкб, МВАр	Мощность активной нагрузки, Рн, МВт
262	80	70	60

Далее представлены исходные данные, одинаковые для всех вариантов:

Система С: Uс = 118 кВ;

Эквивалентный генератор Г представляет собой пять турбогенераторов типа ТВФ-120-2У3 с параметрами каждого из них: Р_номг = 100МВт; U_номг = 10,5 кВ; cosφ = 0,8; R_Г = 0,00186 о.е.; x_d^’ = 0, 278 о.е.; E^’ = 12,5 кВ;

Эквивалентный трансформатор Т1 представляет пять трансформаторов типа ТДЦ-125000 с параметрами каждого из них: S_номТ1 = 125МВA; U_НВ = 242 кВ; U_НН = 10,5 кВ; R_т = 1,42 Ом; x_т = 51,6 Ом.

Эквивалентный трансформатор Т2 представляет пять автотрансформаторов типа АТДЦТН-200000 с параметрами каждого из них: S_номТ1 = 200 МВA; U_НВ = 230 кВ; U_НС = 121 кВ; U_НН = 11 кВ; R_т = 0,57 Ом; x_т = 29,1Ом.

Воздушная линия ВЛ1: провод марки АС-300/39R₀₁ = 0,098Ом/км; x₀₁ = 0,429 Ом/км; L₁ =110 км;

Воздушная линия ВЛ2: провод марки АС-400/51; R₀₂ = 0,075Ом/км; x₀₂ = 0,420 Ом/км; L₂ =140 км.

Ход работы

Выразим исходные данные в системе относительных единиц. Для этого изначально обозначим римскими цифрами номера ступеней трансформации:

I – ступень энергосистемы;

II – ступень присоединения нагрузки;

III – ступень генератора Г;

Считая, что энергосистема, приемные шины которой принимаются в качестве ШБМ, обладает бесконечным регулирующим эффектом нагрузки, что приводит к неизменности напряжения на шинах, задаемся на первой ступени.

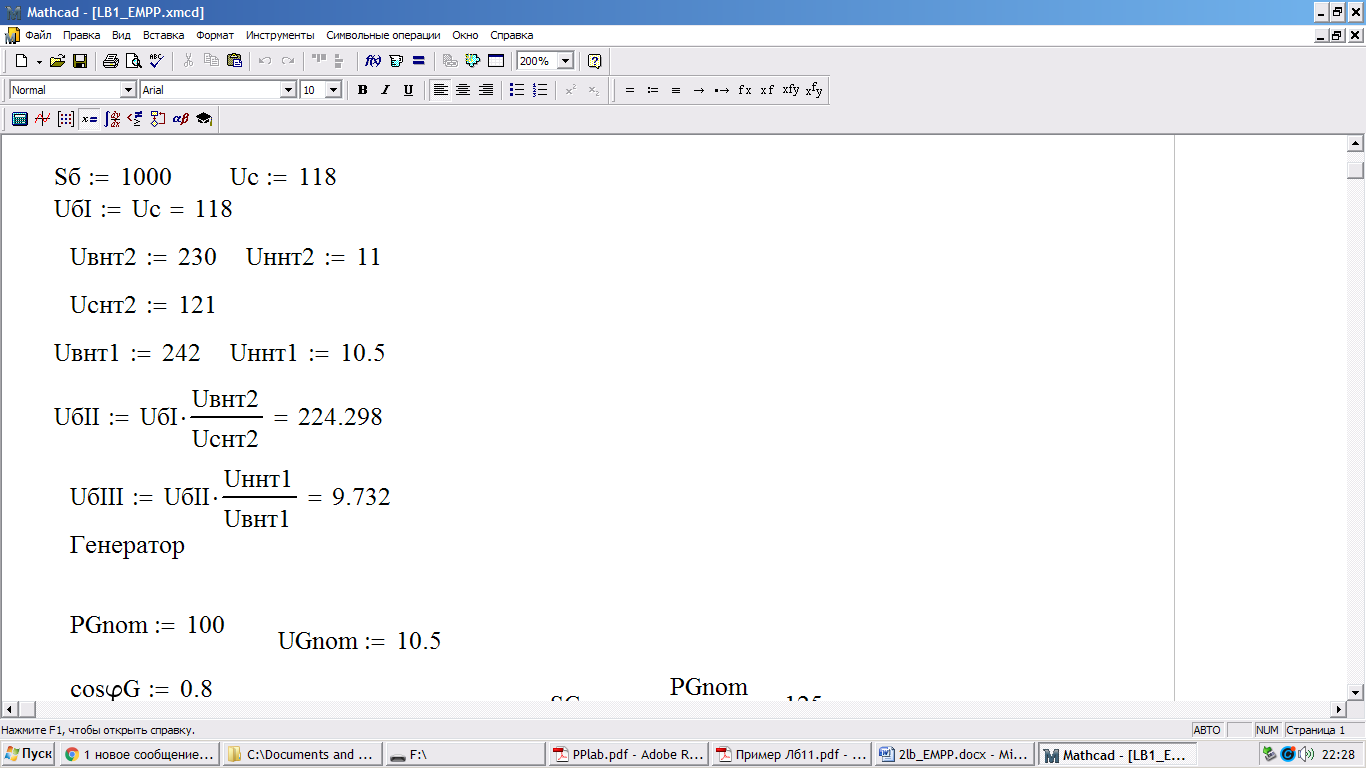
Рассчитать базисные напряжения на остальных ступенях, используя коэффициенты трансформации трансформаторов Т1 и Т2:

Определим номинальные и относительные сопротивления элементов эквивалентной схемы замещения:

Генератор Г:

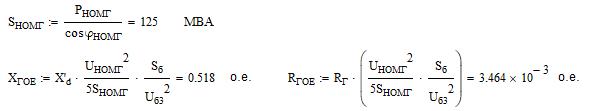
Трансформаторы Т1 и Т2:

Линии ВЛ1 и ВЛ2:

Параметры нагрузки:

Далее выполняем ряд следующих экспериментов:

1. Проведем расчеты угловых характеристик мощности со стороны генератора и со стороны концентрированной энергосистемы (ШБМ) для идеализированной модели энергосистемы без промежуточной нагрузки: P_н = 0; Q_н = 0; R = 0 для всех элементов схемы замещения.

Для этого изначально рассчитаем собственные и взаимные сопротивления:

Находим максимум взаимной мощности и по ней строим функцию мощности генератора, которая также будет являться функцией мощности системы, так как отсутствуют активные потери (рис. 2).

Рисунок 2 – Функция мощности генератора и системы в первом эксперименте

2. Проведем расчеты угловых характеристик со сторон генератора и ШБМ для идеализированной модели энергосистемы при подключении реактора: S_н = jQ_р ; R = 0. Для этого изначально рассчитаем комплексное сопротивление нагрузки:

Находим собственные и взаимные сопротивления, а также их дополняющие углы (которые должны быть равны 0, так как нет активных сопротивлений), при этом используем значения сопротивлений Z1, Z2 из предыдущего пункта:

Так как дополняющее углы равны нулю, то равны нулю и собственные мощности. Находим максимум взаимной мощности, а после чего строим зависимости мощностей генератора и системы (которые будут также одинаковы, так как нет активных потерь) (рис. 3):

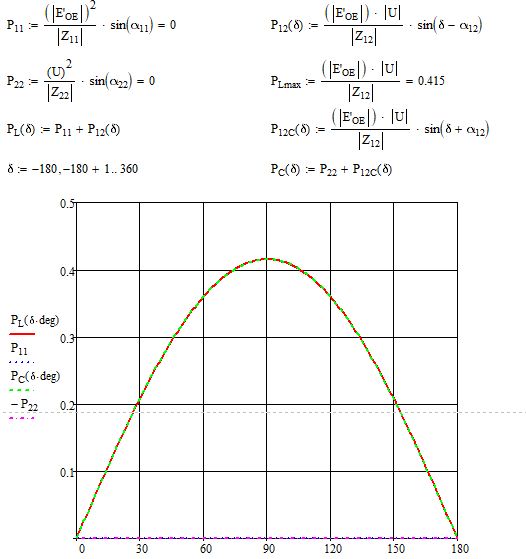
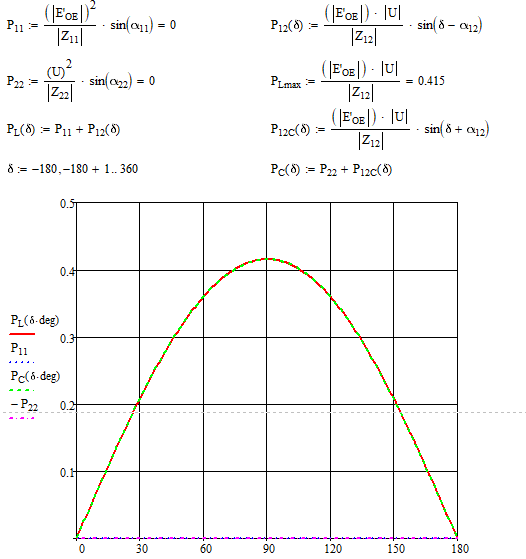Рисунок 3 – Функция мощности генератора и системы при подключении реактора в качестве шунта

3. Проведем расчеты угловых характеристик со сторон генератора и ШБМ для идеализированной модели энергосистемы при подключении конденсаторной батареи: S_н = -jQ_кб ; R = 0. Для этого изначально рассчитаем комплексное сопротивление нагрузки:

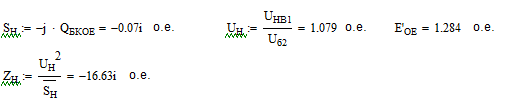
Находим собственные и взаимные сопротивления, а также их дополняющие углы (которые должны быть равны 0, так как нет активных сопротивлений), при этом используем значения сопротивлений Z1, Z2 из предыдущего пункта:

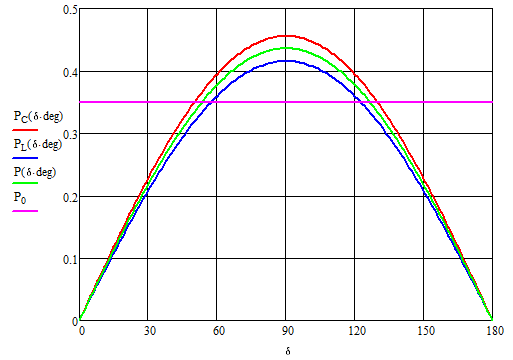
Так как дополняющее углы равны нулю, то равны нулю и собственные мощности. Находим максимум взаимной мощности, а после чего строим зависимости мощностей генератора и системы (которые будут также одинаковы, так как нет активных потерь) (рис. 4):

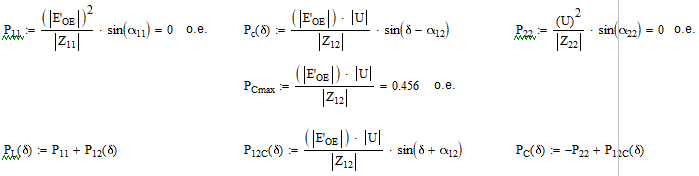
Рисунок 4 – Функция мощности генератора и системы при подключении конденсаторной батареи

По рисунку видим, что максимум мощности выше, чем в предыдущем случае.

На рисунке 5 представим характеристики мощности всех 3 экспериментов.

Рисунок 5 – Функции мощностей генератора

Коэффициенты запаса статической устойчивости:

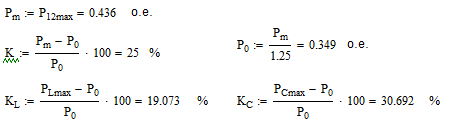
4. Проведем расчеты угловых характеристик со сторон генератора и ШБМ для идеализированной модели энергосистемы при подключении активной нагрузки: S_н = Р_Н. Для этого изначально рассчитаем комплексное сопротивление нагрузки:

Находим собственные и взаимные сопротивления а также их дополняющие углы , при этом используем значения сопротивлений Z1, Z2 из предыдущего пункта:

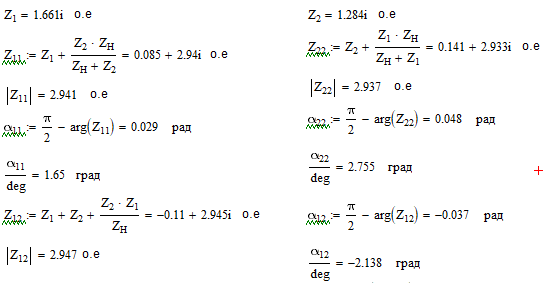
Находим собственные мощности, а после чего находим взаимные мощности и коэффициенты запаса устойчивости, а далее строим зависимости полных мощностей генератора и системы (рис. 6):

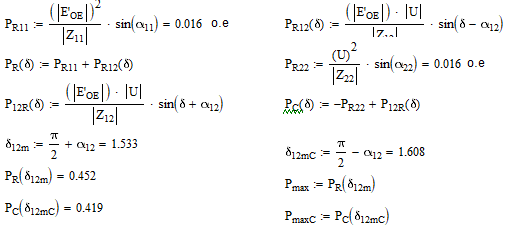
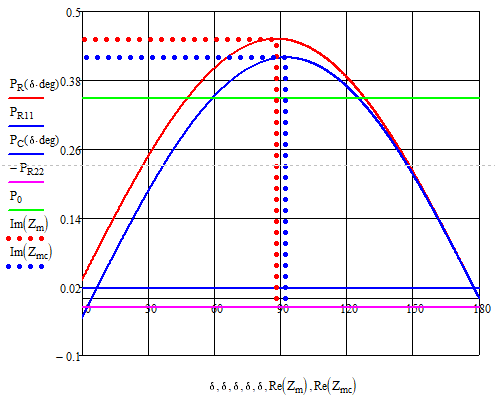Рисунок 6 – Функция мощности генератора и системы при подключении активного сопротивления в качестве шунта

Видим, что характеристика мощности генератора и системы отличаются, что объясняется потерями в активном сопротивлении.

5. Проведем расчеты угловых характеристик со сторон генератора и ШБМ для уточненной модели энергосистемы без промежуточной нагрузки. Для этого изначально пересчитаем комплексные сопротивления:

Находим собственные мощности, а после чего находим взаимные мощности и коэффициенты запаса устойчивости, а далее строим зависимости полных мощностей генератора и системы (рис. 6):

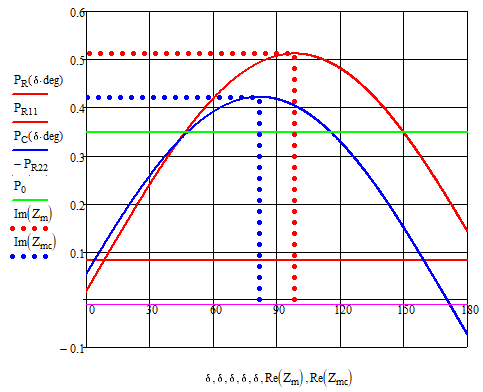Рисунок 7 – Функция мощности генератора и системы при учитывании активных сопротивлений элементов без нагрузки

Видим, что характеристика мощности генератора и системы отличаются, что объясняется потерями в активном сопротивлении.

6. Проведем расчеты угловых характеристик со сторон генератора и ШБМ для уточненной модели энергосистемы при подключении активно-индуктивной нагрузки: S_н = Р_н + jQ_р. Для этого изначально рассчитаем комплексное сопротивление нагрузки:

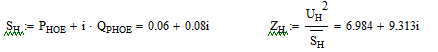
Находим собственные и взаимные сопротивления, а также их дополняющие углы, при этом используем значения сопротивлений Z1, Z2 из предыдущего пункта:

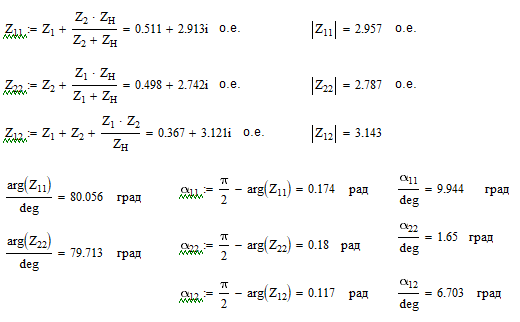
Находим собственные мощности, а после чего находим взаимные мощности и коэффициенты запаса устойчивости, а далее строим зависимости полных мощностей генератора и системы (рис. 7):

Рисунок 8 – Функция мощности генератора и системы при активно-индуктивной нагрузке

7. Проведем расчеты угловых характеристик со сторон генератора и ШБМ для уточненной модели энергосистемы при подключении активно-емкостной нагрузки: S_н = Р_н – jQ_кб. Для этого изначально рассчитаем комплексное сопротивление нагрузки:

Находим собственные и взаимные сопротивления а также их дополняющие углы, при этом используем значения сопротивлений Z1, Z2 из предыдущего пункта:

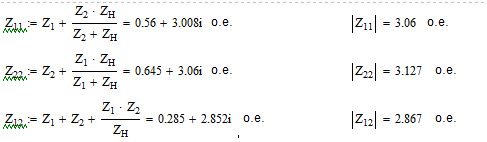
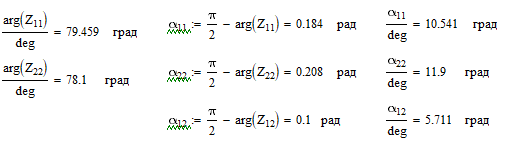
Находим собственные мощности, а после чего находим взаимные мощности и коэффициенты запаса устойчивости, а далее строим зависимости полных мощностей генератора и системы (рис. 9):

Рисунок 9 – Функция мощности генератора и системы при активно-емкостной нагрузке

Вывод

Таким образом, в ходе выполнения данной лабораторной работы были проведены расчеты и анализы статистических характеристик мощности одномашинной энергосистемы. Построены характеристики мощности сначала для идеализированной, а затем и для уточненной системы (учитывая активные сопротивления элементов). Для идеализированной системы характеристики строились для случаев без промежуточной нагрузки, с конденсатором и шунтирующим реактором, а для случая уточненной системы – для случаев с активно-индуктивной и активно-емкостной нагрузкой.

Ответы на контрольные вопросы

1. Практическим критерием статической устойчивости одномашинной системы является положительное значение синхронизирующе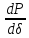й мощности , то есть возрастающий характер характеристики мощности.

2. При подключении шунтирующего реактора предел статической устойчивости будет уменьшаться, потому что реактор будет увеличивать взаимное сопротивление генератора и системы, вследствие чего максимум графика мощности станет ниже, а следовательно уменьшится и запас устойчивости.

3. При подключении конденсаторной батареи взаимное сопротивление, наоборот, уменьшается, поэтому в этом случаем максимум мощности возрастет, а вместе с ним и коэффициент устойчивости.

4. В уточненной модели характеристики мощности генератора и системы не будут совпадать, так как часть мощности будет теряться на активных сопротивлениях.

5. Дополняющий угол может быть отрицательным только у взаимного сопротивления, так как взаимное сопротивление характеризует лишь коэффициент пропорциональности между ЭДС в одной ветви и током в другой ветви.

6. Дополняющие углы собственных сопротивлений не могут быть отрицательными, так как они характеризуют отношение между ЭДС и током в одной ветви, то есть определяют активное сопротивление, которое физически не может быть отрицательным.