50. Теоремы о среднем (Ролля, Лагранжа и Коши) их геометрическая интерпритация.

Теорема Ролля. Если функцияf(x) непрерывна на отрезке[a, b], дифференцируема на интервале(а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале(а, b) существует точка ε, a < ε< b, в которой производная функция f(x) равная нулю, f′(ε)=0. Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a,b) существует точка ε такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Теорема Ролля является частным случаем теоремы Лагранжа.

Теорема Лагранжа. Если функцияf(x) непрерывна на отрезке[a,b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка ε такая, что

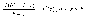Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке

Это выражение называется формулой Лагранжа или формулой конечных приращений.

Геометрический смысл теоремы состоит в том, что отношение равно угловому коэффициенту секущей АВ. Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка ε такая, что в соответствующей точке кривой y = f(x)касательная параллельна секущей, соединяющей точки А и В. Таких точекможет быть и несколько, но одна существует точно.

Теорема Коши. Если функции f(x) иg(x) непрерывны на отрезке[a, b] и

дифференцируемы на интервале(a,b) и g′(x) ≠0 на интервале(a,b), то

существует по крайней мере одна точка ε, a < ε< b, такая, что

Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке ε.

Теорема Лагранжа является частным случаем (при g(x)=x) теоремы Коши.

49. Производные и дифференциалы высших порядков

Пусть функция f(x) – дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную.

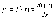
Если найти производную функции f′(x), получим вторую производную функции f(x).

Этот процесс можно продолжить и далее, находя производные порядка n.

При этом под производной нулевого порядка подразумевается сама функция

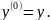
48. Дифференциал функции. Инвариантная форма записи дифференциала.

Дифференциалом функции f(x) в точке х0 называется главная линейная часть приращения функции. Дифференциал функции f(x) в точке х0 обозначается символом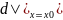 или df(x0).Он имеет вид в этой точке dy|x0=f’(x)*dx, где dx – дифференциал независимой переменной. (dx=∆x – только для независимой переменной).

Дифференциал сложной функции y=f(x), для которой x=ϕ(t), имеет такой же вид, dy=f”(x)dx, как и в том случае, когда аргумент x является независимой переменной. Это свойство называется – инвариантность формы дифференциала.

47.Применение дифференциала для приближенных вычислений

Приращение 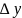функции 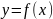представимо в виде:

где функция 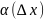является б.м. функцией при стремлении аргумента 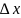к нулю. Так как 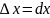, то

В силу того, что второе слагаемое 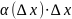является бесконечно малым, то им можно пренебречь, а поэтому

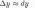
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.

Для приближенного вычисления значения функции применяется следующая формула:

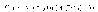
46. Дифференциал функции. Геометрический смысл дифференциала, его свойства

Дифференциалом функции f(x) в точке х0 называется главная линейная часть приращения функции. Дифференциал функции f(x) в точке х0 обозначается символом или df(x0).Он имеет вид в этой точке dy|x0=f’(x)*dx, где dx – дифференциал независимой переменной. (dx=∆x – только для независимой переменной).

Дифференциал функции в точке х0 равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента ∆x. Поэтому замена ∆y на dy геометрически означает замену участка кривой участком ее касательной.

Если u= f(x) и v= g(x) есть функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1) d(u ±v) = (u ±v)′dx = u′dx ±v′dx = du ±dv

2) d(uv) = (uv)′dx = (u′v + v′u)dx = vdu + udv

3) d(Cu) = Cdu

4)

30.Бесконечно большие функции и их связь с бесконечно малыми функциями

Функция называется бесконечно большой при х→а, где а – число или одна из величин ∞, +∞ или-∞, если 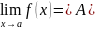, где А – одна из величин ∞, +∞ или-∞.

Связь бесконечно больших и бесконечно малых функций отражена в следующей теоремой.

Теорема. Если f(x)→0 при х→а (если х→∞) и не обращается в ноль, то

31.Основные теоремы о пределах

- №1

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х→а.

2.Предел суммы/разности двух функций равен сумме/разности их пределов

3.Предел произведения двух функций равен произведению их пределов:

4.Следствие формул 1 и 3:константу можно выносить за знак предела:

Константу можно выносить за знак предела.

5.Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

,(№6) если эти пределы не равны 0.

7.Если f(x)>0 вблизи точки х= а и , то А>0.Аналогично определяется знак предела при f(x) < 0, f(x) ≥0, f(x) ≤0.

8.Лемма о двух полицеских .Если g (x)≤ f(x) ≤ u(x) вблизи точки

х = а и

, то и .

9.Если функция f(x) имеет конечный предел при х→а, то она ограничена вблизи точки х = а. Функция f(x) называется ограниченной вблизи точки х= а, если

существует такое число М>0, что ⎪f(x)⎪<M вблизи точки х= а.

33.Первый замечательный предел .

Для раскрытия неопределенностей 0/0 содержащие тригонометрические функции необходимо установить справедливость важной формулы

.

Следствие1.

Следствие2.

Следствие3.

Следствие4.

Следствие5.

Следствие6.

Следствие7.

Замечание.Следствия1–3, а следствия5,6 доказывают истинность первых трех и двух последних строчек в таблице эквивалентных функций при

х→ а Часто если непосредственное нахождение предела какой-либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.